收益和风险概念

第一节　收益和风险概念

在现实经济中，由于项目未来的投资收益具有不确定性，因此，项目都是有风险的投资项目。本节介绍收益的各种不同表达形式和收益不确定性的各种衡量指标。

一、收益

1．收益和收益率的基本含义

则项目在投资期间实现的投资收益额为相应的投资收益率为

式（3－2）所定义的投资收益率是指整个投资期间实现的收益率，又称为“持有期收益率”（Holding Period Return）。由于不同投资项目的投资期限各不相同，因此，无法用持续期收益率来评估不同期限项目的优劣。为了使不同投资期间的投资收益率具有可比性，就有必要对投资收益率代表的投资期间规定统一的时间长度。在实际操作中，通常以1年为一个标准的时间单位，计算相应的投资收益率。为此，我们可以给出投资收益率的标准化定义为

式（3－3）中，r_t表示第t年（从时点t－1至时点t的期间）的收益率，P_t表示资产（或某项投资）在第t年末（时点t）的价格，C_t表示资产（或某项投资）在第t年间获得的收益，t－1（时点）表示投资初始时刻。

在不同的投资策略下，对项目存续期内获得的现金流量再投资有着不同的假设，因此，不同投资策略下的持有期收益率和各年收益率会出现差异。式（3－2）实际上隐含一个重要的假设，即对存续期内获得的各期投资收益不再进行追加投资。如果将项目存续期内所获得的现金流进行再投资，则“持有期收益率”的定义为

在这样的持有期收益率定义下，假如某项投资的投资年限为N年，则该项投资在N年间实现的“持有期收益率”与各年收益率的关系为

式（3－5）表明，在投资期间内实现的“持有期收益率”，是投资期间内各期实现的收益率的乘积。

我们还可以用年平均收益率（Average Rate of Return）表示投资收益状况。平均收益率通常有两种计算方法。一种是“算术平均法”（Arithmetic Averaging），另一种是“几何平均法”（Geometric Averaging）。

如果投资期内所获得的现金流量不进行再投资，则年均收益率可以用“算术平均法”计算，即

式（3－6）中，r_AA表示按算术平均法计算出的年平均收益率，N表示投资的期限数，r_t表示t期的收益率。

如果投资期内所获得的现金流量进行再投资，则年均收益率可以用“几何平均法”计算，即

上式中，r_GA表示按几何平均法计算出的年平均收益率，r表示持续期收益率。

2．期望收益率

“期望收益率”（Expected Rate of Return）是指人们对未来投资所能产生的投资收益率的预期。在未来的经营中，存在着诸多的不确定性因素，目标项目投资收益率并不会是一个确定的值。因此，我们在当前时刻考察未来t时刻的投资收益率时，实际上观察的是一个随机变量，即

式（3－8）中，有关变量上的“～”表示该变量是一个随机变量。

由于未来投资收益率的不确定性，我们只能用在未来平均状态下可以获得的收益率，即目标项目未来投资收益率的均值，作为该项目的“期望收益率”。即

如果假设未来投资收益率与已实现的投资收益率分布于同一个概率空间，并且是独立同分布的，那么可以用观察到的已实现投资收益率的样本均值，作为未来投资期望收益率的无偏估计量，即

算术平均收益率可作为期望收益率的估计值，其理由是，它在经济意义上有较强的解释力，并获得了统计上的支持。几何平均收益率的准确经济含义是，它表示的仅仅是历史的、已经实现的、以复利计算为基础的年平均收益率，并不是历史投资收益率的样本均值，因而也就无法成为未来投资期望收益率的估计值。

3．要求收益率

要求收益率（Required Rate of Return）是指投资者在进行某一项投资时所要求的回报率，该收益率是投资者在主观上提出并要求的，因而具有主观性。而期望收益率是客观的，是由市场的客观交易条件决定的，即在当前市场价格水平下可以由市场向投资者真实提供的。

假如资本市场上的交易价格可以自由变动，市场可以在无套利的条件下形成均衡价格时，则对某一项投资而言，投资者的要求收益率与在均衡价格下该投资所提供的期望收益率是相等的，套利行为很快会消除这种差异。即

式（3－11）中，r_R表示要求收益率，r_E表示期望收益率。

我们可用以下推理过程加以说明。假如某项投资产生的投资收益是一次性的，且出现在N年之后，记为CFN，则对投资者而言，在要求收益率为r_R时，其愿意出的最高买价格PBID为

如果将此时出售者的卖出价格记为PASK，即

当PASK大于PBID时，r_R＞r_E，此时市场上的交易无法达成。如果有投资者愿意购买，则对出售者而言，存在着套利的机会。出售者会持续卖出该项投资，压低交易价格，直至套利机会消失。而当PASK小于PBID时，r_R＜r_E，可以使投资者获得一个套利的机会，促使交易价格上升。只有当PASK等于PBID时，价格才能达到均衡，并且此时对投资者和出售者而言均不会存在任何的套利机会。如果投资的收益是在N年内多次发生的，我们同样可以根据以上逻辑推导出此定理。

在现实经济生活中，当证券提供的期望收益率与投资者的要求收益率不一致，而市场又不能自动进行价格调节时，会出现发行价格高估（期望收益率低于要求收益率）的情况，造成证券无法顺利发放出去。反之，会出现承销商惜售，普通投资者难以按发行价格购买证券。因此，公司在融资时，应该根据要求收益率确定有关证券的发行价格，以便使新发行证券所提供的期望收益率与投资者的要求收益率正好吻合，保证有关证券发行的顺利完成。

只有在价格自由变动的市场交易环境下，无套利的市场均衡价格才会保证此时的要求收益率和期望收益率在数值上是相等的。而正是这一点，使我们可以根据资本市场上的历史交易价格数据，计算未来期望收益率估计值，并以此作为投资者要求收益率的估计值。

二、风险及其度量

1．风险

金融学中的“风险”（Risk）是指未来状态或结果的不确定性，并不涉及由该不确定性（或风险）所造成的后果。在进行项目投资时，如果在当前时刻能够获知未来投资回报的准确金额，而且在未来获得该投资回报时，不存在任何的不确定因素，那么我们称目标项目是无风险的投资项目。反之，如果在当前时刻只能获悉未来投资收益的期望值，而且具体的实现值是不确定的，存在着多种可能性，那么目标项目便是一项有风险的投资项目。

2．风险度量

（1）方差和标准差

在度量投资风险时，人们常常是依据投资收益率的最终可能实现值偏离期望值的程度来判断投资的风险大小。评价风险大小的方法很多，其中最常用的是方差和标准差。设未来的收益率为r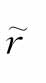，其各种状态发生的概率为P_i，则方差σ²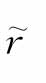（）与标准差σ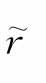（）的计算公式分别是：

（2）协方差和相关系数

协方差（Covariance）是度量一种证券收益和另一种证券收益之间相互关系的指标，其公式为

相关系数（Correlation）表示两种证券收益率的相关性。可用公式表示为