关于几种形式的中国部门生产函数的齐次性检验

关于几种形式的中国部门生产函数的齐次性检验_纪念中国社会科学院建院三十周年学术论文集·数量经济与技术经济研究所卷

关于几种形式的中国部门生产函数的齐次性检验

汪同三　张昕竹

一、概述

近几十年来关于生产函数的研究结果表明，需要全面考虑各种投入要素——资本(K)、劳动力(L)、能源投入(E)和其他原材料投入(M)——对产出的影响。对真实生产函数

的二阶近似在生产理论和生产函数的应用研究中具有重要意义。一个生产函数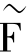是F的二阶近似则必须在定义域的任何点满足:

F=F

▽²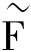=▽²F

另一种二阶近似的解释是Taylor展开近似，设X=(x₁，…，x_n)为包括K，L，E，M在内的n种生产过程的投入要素，真实生产函数具有如下形式:

其中f₁，…，f_n分别为x₁，…，x_n的任意二次可微变换，则通过对(1.3)式的二次可微变换，有:

对于(f₁(x₁)，…，f_n(x_n))，(1.4)式的Taylor展开为

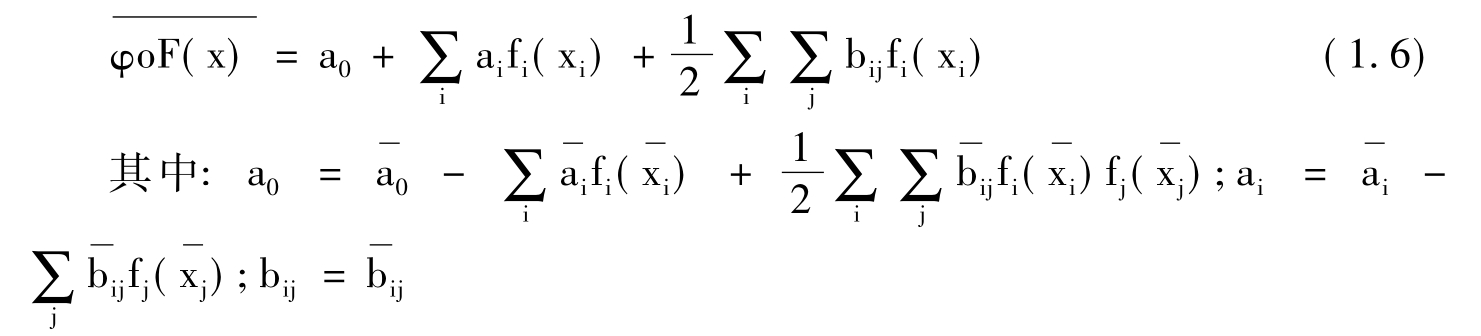
福斯(Fuss)等人总结了7种主要的参数线性形式的生产函数。其中:

1.C－D函数

其中:φ(y)=logy，f_i(x_i)=logx_i并限制b_ij=0，(i，j=1，…，n)。

2.CES函数

式中:φ(y)=y^－ρ，f(x)=，并限制b_ij=0，(i，j，=1，…，n)。当然，当ρ未知时，(1.8)式是参数非线性形式。

3.Translog(超越对数型)函数

式中:φ(y)=logy，f_i(x_i)=logx_i。

4.G－L(广义线性－Generalized linear)函数

式中:φ(y)=y，f_i(x_i)=。

以上函数形式是福斯等人所列举的7种参数线性形式的生产函数中的4种，当它们的系数a₀，a_i，b_ij满足特定条件时，函数具有线性齐次性。(另外广义C－D函数也能在某种限制条件下满足线性齐次性及二阶近似形式的对称性，本文未予讨论)。本文的工作就是利用中国7个部门的有关数据估计上述4种生产函数的KLEM形式的参数，并对它们各自的一阶齐次性和对称性做检验(这7个部门的序号见表1)。

表1

二、估计和检验方法

对于C－D和CES两个一阶近似函数，可以直接从函数原型估计参数，而对Translog和G－L两个二阶近似函数，则应从生产的平衡条件，即要素投入份额与产出对投入的弹性相等来估计参数。要素投入份额为

式中:p_i为投入要素价格;q为产出价格。而产出对投入的弹性为

则平衡条件为:

且有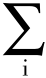V_i=1。

7个部门的V_E，V_M可以根据各部门的能源和其他中间投入的价值量直接计算，V_L由P_Ll/qy计算，其中P_L为人均年工资额，V_K由1－V_E－V_MV_L计算得到。我们的数据样本从1966年到1987年共22个。在我们的工作中，(2.3)式是由若干个方程组成的联立方程组，我们使用的是三阶段最小二乘法(3SLS)以得到参数的联立估计值。

我们的参数估计分两个步骤:第一步，对原型函数(一阶近似条件下)或(2.3)式(二阶近似条件下)做无约束参数估计，得到a₀，a_i(i=K，L，E，M)(在一阶近似条件下)或，a₀，a_i，b_ij(i，j=K，L，E，M)(在二阶近似条件下)的估计值。第二步，在齐次性限制条件下得到上述各参数的有限制的估计值。

为简单起见，我们以一阶近似为例讨论有关的有限制参数估计和检验问题，在此情形下，(1.6)式简化为

设Y=(y₁，…，y_n)为(2.4)左端的数据向量，这里n为样本数; X为(2.4)式右端的由1和f_i(x_i)生成的数据矩阵(n×m阵，m为参数个数)，γ为参数向量(m维)。则(2.4)式的估计方程为

这里u～N(0，σ²I_n)，u=(u₁，…，u_n)，u_i与u_j独立(i≠j)。

由于齐次性和对称性限制条件可以化为一组等式约束，因此限制条件下的估计方程为

式中:Hγ=c为限制条件;且秩(H)=q≤m;秩(X)=m;c为m维向量。

在有限制条件下的参数估计实际上是求解下述二次规划问题

服从F(q，n－m)分布。

更一般地，如果(2.6)式中增加另一限制

H₁γ=c₁且　　秩(H₁)=q₁

服从F(q₁－q，n－m+q)分布。

一方面由于CES函数在ρ未定时不是参数线性的函数，故需要采用迭代的非线性估计方法;另一方面，CES的参数估计是单方程的，因此，对CES函数的齐次性及一阶齐次性检验采用的是t检验方法(这将在第四节中讨论)。

三、C－D函数

C－D函数最早是柯布－道格拉斯由经验研究发现的，在那里仅考虑了资本和劳动力两种投入要素。后来多马将C－D函数推广到多投入要素的形式。C－D函数的KLEM形式为

其一阶线性齐次条件为

关于C－D函数的无限制与有限制条件下的参数估计值及有关的统计检验值和(2.8)式所示的F检验结果见表2(见附表)。这里有5个部门的n=22，m=5，q=1，所以(2.8)式所示统计量服从F(1，17)分布。其他两个部门——非能源重工业和工业因为样本期内有关变量的数据序列波动过于剧烈，我们做了一些必要的野点舍弃，这两个部门的n分别为12和18。表2的1－5列中，每个部门的第一行数据为无限制的(3.1)式的参数估计值，第二行为在(3.2)式限制下的参数估计值，表中第二—五列括号中的数字为有关参数的t检验值。第六列S²与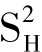分别为无限制条件和有限制条件下的拟合值残差平方和，第七列F为(2.8)式所示F值，第八列f.d为(2.8)式所示的自由度，第九列α_0.01为相应自由度的F检验的临界值和显著性水平。表中的e表示可由限制条件推导得出的参数(以下各表中除特别说明外，意义相同)。

表2表明，除工业部门为，其他6个部门均通过了f检验，即一阶齐次性限制条件下的参数估计与无限制的参数估计没有显著性区别。这说明就C－D生产函数而言，规模收益不变在中国的多数生产部门中是较为普遍的情况，而总量程度较高的部门划分(工业)则出现非规模收益不变的情况，其中轻工业的一阶齐次性最为明显。表中某些部门的a_K，a_L，a_E出现负数，这是中国部门C－D生产函数经常出现的问题，但除了重工业部门的无限制的a_L，不包括能源工业的重工业的有限制的a_L，以及运输邮电部门的有限制的a_E外，其他7个负值参数的t检验值均说明它们与0无显著性区别。

四、CES函数

阿罗(Arrow)等人提出的两投入要素的CES生产函数为:

这一形式是一阶齐次的，以后(4.1)式又被推广为u阶齐次的

当u≠1时，它是非不变规模收益的，但仍保留齐次性。尤赞瓦(Uzawa)将(4.2)式推广为多投入要素的情况

其中要求a_i＞0，(i=1，…，n)，ρ＞－1。

与前面的(1.8)式相比较，我们检验的CES函数的KLEM形式为:

同样要求，均大于0，且ρ＞－1。为了保证上述条件被满足，我们对下式进行估计:

这里S(a₀)为估计值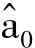的标准误差，n=22，m=7。

其次对(4.4)式进行一阶齐次性检验，即假设检验为H_0∶∶u=1统计量为:

其中:S(u)为估计值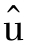的标准差。

当取显著性水平α=0.02时，临界值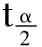(15)为2.602。在(4.6)和(4.7)式中，当T_a0或T_u大于2.062时拒绝H_0∶∶a₀=0或u=1。表3(见附表)给出7个部门的CES函数(4.4)式的参数估计值和两个t检验值，表中所示内容如前节所述。

由表3可以看出，中国7个产业部门的KLEM形式的CES函数均不仅能通过齐次性检验，而且能通过一次齐次性检验。这说明用CES函数研究中国的部门生产的规模收益性质是很有价值的。

五、超越对数型函数

(1.9)式所示的，由克里斯滕森、乔根森、刘遵义提出的超越对数型生产函数是对真实生产函数的一种二阶近似形式。它的KLME形式为:

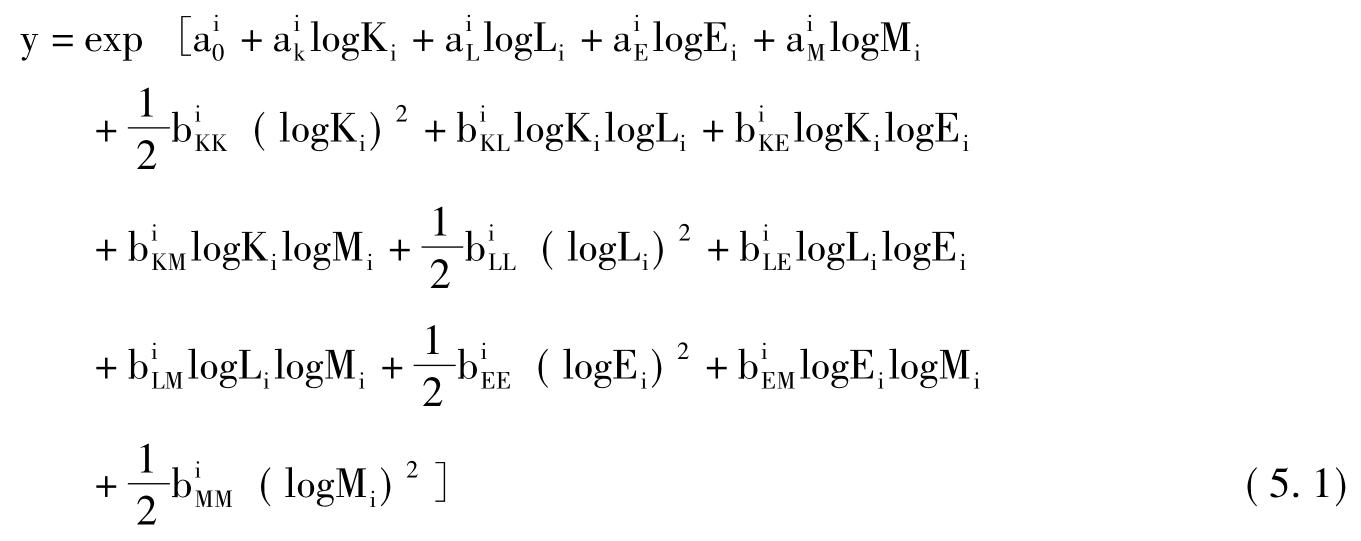
由(2.1)—(2.3)式给出的平衡条件为:

(5.1)式的对称性条件为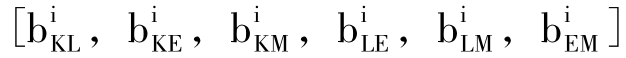在(5.2)式中的两次出现必须相等。(5.1)式的一阶齐次性充分必要条件为:

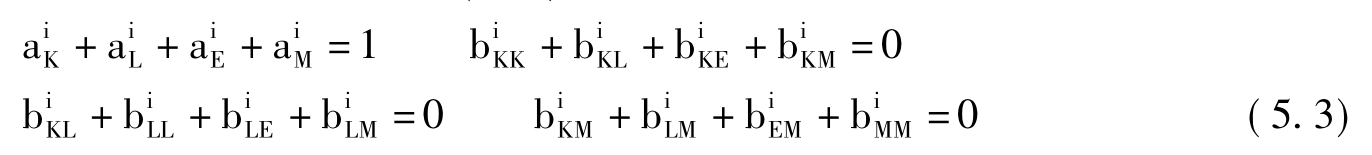
由(5.3)式可以得到，超越对数型生产函数的对称性和一阶齐次性条件是相互等价的，因此对它的对称性和一阶齐次性检验可以一并完成。

由于在(5.3)式条件下，(5.2)式中任一方程可以由其他三个方程得到，这里我们选择后三个方程进行估计。对(5.2)式的参数我们用三阶段最小二乘法联立估计，估计结果见表4。表4中15个参数的第一行是无限制的参数估计值，第二行是在条件(5.3)限制下的参数估计值，其中e表示限制，即在已知其他参数值的条件下，它们可由(5.2)及(5.3)式得出。表中的S²和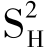分别为无限制条件下的拟合残差平方的加权和，这里我们所估计的三个方程的权数分别为V_L/(1－V_K)，V_E/(1－V_K)，V_M/(1－V_K)，显然有

V_L/(1－V_K)+V_E/(1－V_K)+V_M/(1－V_K)=1

式中γ=(γ_L，γ_E，γ_M)^T，=()为拟合值向量。

为权数对角阵。同样可得到。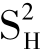

表4(见附表)中F值由(2.8)式计算得到，其中q=6，n=22×3=66，m=5×3=15，F检验的第一，第二自由度分别为6和51。检验结果表明只有轻工业部门通过了对称性和一阶齐次性检验。

六、G－L函数

(1.10)式所示由狄沃特提出的广义线性函数，也是对真实生产函数的一种二阶近似。它的KLEM形式为

由(2.1)—(2.3)式给出的平衡条件为:

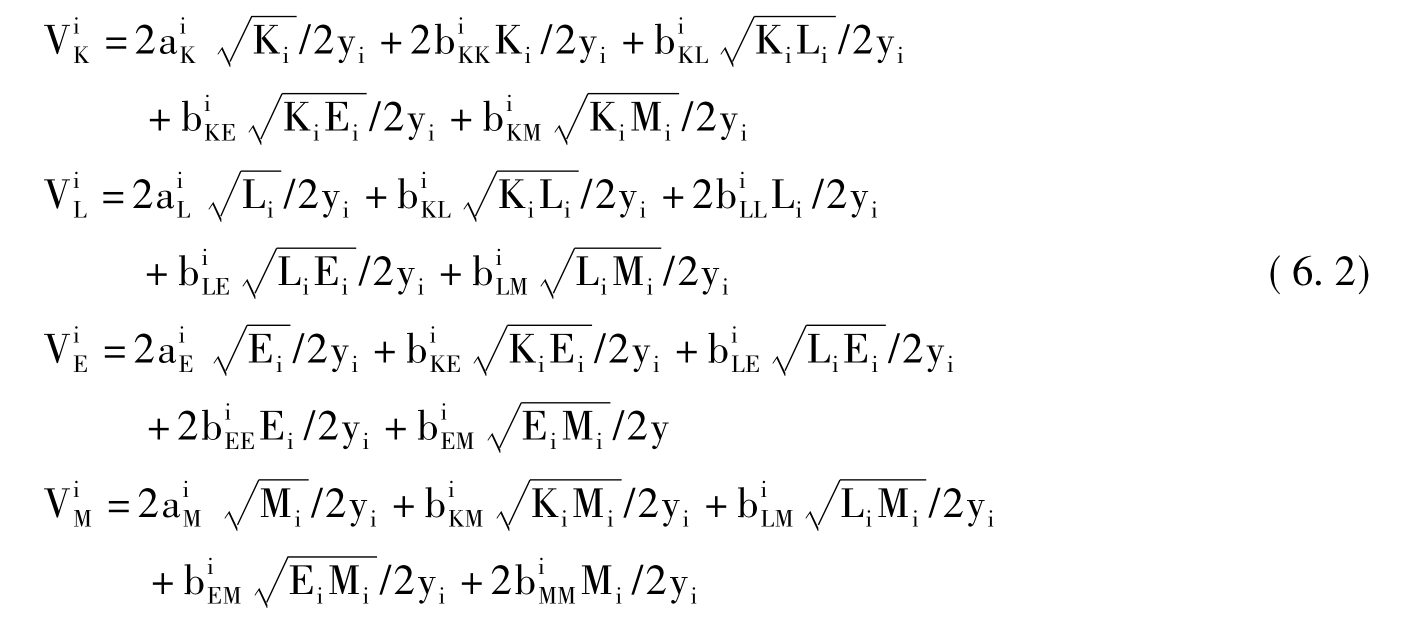
(6.1)式的对称性条件为［b_KL，b_KE，b_KM，b_LE，b_LM，b_EM］在(6.2)中的两次出现必须相等，也就是说(6.1)式的Hessian矩阵是对称的。(6.1)式的一阶齐次性的充分必要条件为:

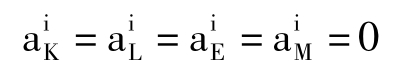
由V_K+V_L+V_E+V_M=1及(6.2)得=0，这里我们需要对(6.2)中全部方程进行估计。与超越对数型函数不同的是广义线性函数的对称性与一阶齐次性不等价，因此对这两种性质考虑分别检验。这里我们进行三次检验，即

检验Ⅰ:无限制→对称性;检验Ⅱ:无限制→一阶齐次性;检验Ⅲ:无限制→对称性→一阶齐次性。

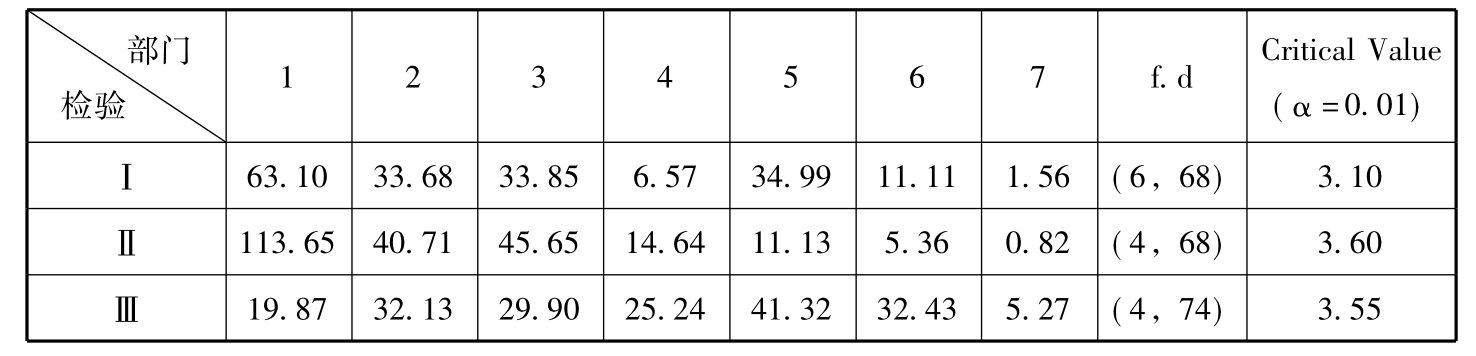
检验Ⅰ和Ⅱ的F值计算公式使用(2.8)式，检验Ⅲ的F值计算公式使用(2.9)式。在三个检验中n=22×4=88，m=5×4=20，而检验Ⅰ中的q=6，检验Ⅱ中q=4，检验Ⅲ中q₁=10，q=6，因此在三个检验中第一、第二自由度分别为(6，68)，(4，68)，(4，74)。

对(6.2)式仍用了3SLS法联立估计参数值，7个部门的无限制估计值(0)，对称性限制估计值(Ⅰ)，一阶齐次性限制估计值(Ⅱ)以及同时满足对称性限制和一阶齐次性限制估计值(Ⅲ)分别见表5.1—5.7(见附表)的第1—4列。上述7个表中e仍表示限制，即它们的值可由对称性或一阶齐次性条件得出，表中的S²，分别为无限制、对称性限制、一阶齐次性限制、同时对称性和一阶齐次性限制的拟合值残差平方的加权和，其表达式类似于(5.4)式。

各部门的检验，Ⅰ，Ⅱ，Ⅲ的F值见表6，检验结果表明只有商业部门通过了相对于无限制的对称性检验和一阶齐次性检验。

表2

七、拟合优度的显著性检验

轻工业部门的C－D、CES和Translog函数均通过了一阶齐次性检验。这样我们可以通过F检验来检验这三种函数的拟合效果两两之间是否存在显著性区别，其统计量为

在拟合误差满足正态性和独立性时上述统计量服从，F(n_i－1，n_j－1)分布。

轻工业部门的上述三种函数的F检验值见表7。结果表明，除了CES和Translog之间存在显著性差别外，其他函数形式两两间其拟合效果不存在显著性区别。

表3

同样，商业部门的C－D、CES和G－L函数均通过了一阶齐次性检验，我们也可以通过F检验来检验这几种函数的拟合效果两两之间是否存在显著性差别。检验结果见表8。结果表明，三种函数两两之间均不存在拟合效果的显著性区别。

表4

上述两个检验结果说明，至少在函数满足一阶齐次性和/或对称性条件时，一阶近似函数和某些二阶近似函数有基本相似的拟合效果。这为我们根据研究对象的不同特点和研究工作的不同目的选择不同的生产函数形式提供了较宽的余地。

八、总结

1.本文讨论了中国7个部门生产函数的4种形式的参数估计和一阶齐次性及对称性检验。我们发现C－D函数在划分较细的6个部门中均能满足一阶齐次性条件，CES函数在7个部门中均能满足一阶齐次性条件，而两个二阶近似的Translog函数和G－L函数分别只在一个部门的生产函数中满足一阶齐次性。

2.我们的检验结果表明，总量水平较高的部门(如重工业)的生产函数距离我们所检验的性质较远，而非总量水平较高的部门(如轻工业)的生产函数距离我们所检验的性质较近。这与理论生产函数所具有的多数性质是由微观层次的分析得来的有关，同时说明了在中国的有计划的商品经济中，生产函数的部门加总问题需要进一步研究。

3.Translog函数和G－L函数分别在轻工业和商业部门通过了一阶齐次性及对称性检验，这是一个十分有趣的现象。两个二阶近似函数的参数估计是以要素投入份额与产出对投入的弹性相等这一平衡条件为基础的，而这一平衡条件反映的是新古典主义的价格调整、市场均衡原则。在中国，轻工业和商业的生产显然是与市场状况联系较密切的，因此，这两个部门的二阶近似生产函数更有可能满足平衡条件，进而满足一阶齐次性和/或对称性条件。本文所讨论的其他部门，如重工业、建筑业、运输邮电业显然较轻工业和商业对市场机制不敏感，具有较强的计划经济性质，因此这些部门的二阶近似生产函数难以通过齐次性和/或对称性检验便不足为奇了。

4.由于中国的有计划的商品经济与西方国家的市场经济机制存在着质的区别，因此，结合中国的具体特点，借鉴西方生产理论的研究成果，以数量分析为基础发展适合中国国情的生产函数的理论和应用研究是我们的一项重要的科研任务。

［参考文献］

1.M.Fuss，D.McFadden，Y.Mundlak:“A Survey of Functional Forms in the Economic Analysis of Production”，M.Fuss，D.McFadden ed: Production Economics: A Dual Approach to Theory and Applications，voll，1979

2.C.Cobb，p，Douglas，“a Theory of Production”American Economic Review，18(1928)，p139－165

3.E.Domar，“On the Measurement of Technological Change”，Economic Journal，71(1961)，p709－729

4.K.Arrow，H.Chenery，B.Minhas，R.Solow:“Capial－labour Substitution and Economic Efficiency”Review of Economics and Statistics，43(1961)，p225－250

5.M.Intriligator: Economic Models，Techniques and Applications1978，p276－277

6.H.Uzawa:“Production Functions With Constant Elasticities of Substitution”，Review of Economic Studies，29(1962)，p291－299

7.L.Christensen，D.Jorenson，L.Lau:“Conjugate duality and transcendental logarithmic production function”，Econometrica，39(1971)，p255－256

8.L.Lapin Statistics for Modern Business Decisions，3rd，1982，ch.16

(原载《数量经济技术经济研究》1990年第4期)