经济增长模型中的储蓄率内生化问题
贺菊煌
在索洛经济增长模型中,储蓄率是作为外生变量处理的,这使得它在理论上欠完美,在应用上受到了限制。因此,一些经济学家致力于增长模型的储蓄率内生化研究,取得了不少有价值的成果,但都不完善。本文拟对这方面的问题进行讨论。
储蓄率内生化的基本方法是将个人消费的跨时优化纳入模型之中。其中有3个关键点:①跨时效用函数。②个人寿命。③未来收入的预期。
关于第1点,现有的大多数文献采用时际可加的常数边际效用弹性函数。我们也认为这样的函数比较合理,因此本文不再讨论。关于第2点和第3点,在现有文献中流行的假定有的离实际很远,使得与它们相联系的模型得出的一些结论不正确。所以本文将集中注意力对这两方面的问题进行讨论。
一、关于个人寿命
(一)个人消费跨时优化中的寿命假定
在现有的关于个人消费的跨时优化模型中,对于人的寿命有以下几种假定:
1.确定的无限寿命。即假定人们永远不死,它被许多经济模型采用,例如Cass-Koopmans模型。
2.不确定的无限寿命。即假定人们可能生存无限长的时间,但人们在任何时期都有一个不变的、大于0小于1的死亡概率。见于布兰查德和费希尔《宏观经济学》中的“永葆青春模型”。
3.确定的有限寿命。即假定人们在某个确定的较大年龄以前,死亡概率为零;在到达这个确定的较大年龄以后,死亡概率为1,它也被许多经济模型采用,例如Modigliani的生命周期模型,Diamond的世代交叠模型。
4.不确定的有限寿命。即人们有一个最大可能年龄;在到达最大可能年龄以前,在每个年龄上都有一个大于0小于1的死亡概率,而且除了婴幼儿阶段和少年阶段,死亡概率随年龄的增大而增大;在到达最大可能年龄以后,死亡概率为1。由于其复杂性,现有文献没有把这种寿命假定纳入经济增长模型之中;只有少量文献把这种寿命假定纳入遗产问题的研究之中。
前两种假定离实际很远;第3种假定离实际较远;第4种假定切合实际,而且与人口结构进入经济模型相适应。许多经济问题的研究涉及人口结构问题,例如人口变动对储蓄率的影响、社会养老保险等问题的研究,都涉及人口结构问题。在经济模型中引入人口结构,起码需要引入分年龄的人口死亡率,这就意味着个人寿命的不确定性。所以,在消费的跨时优化中引入不确定有限寿命,是人口结构进入经济模型的逻辑延伸。
(二)不确定寿命下的消费决策方法
在现有文献中,对于不确定有限寿命下的消费决策,学者们提出的基本方法是:把存活概率作为贴现因子之一纳入跨时效用函数之中,其优化的时间区间仍然采取确定寿命模型所用的固定终点的区间。我们认为,这样的方法不正确。因为,在不确定寿命下,人的死亡年龄不是常数,而是随机变量;因此消费的跨时优化的时间区间的终点不是常数,而是随机变量。与此相对应的概率,不是存活概率,而是余年(还能活多长时间)概率。这两种概率的区别见图1、图2。
我们认为,在寿命不确定条件下,个人消费决策可取以下两种方法:
1.“余年分析法”。这种方法将消费决策分三步:
第一步,计算余年(未来可能的生存时间)的概率分布。在寿命不确定条件下,每个年龄的人的余年都是随机变量,其概率分布可根据分年龄的人口死亡率表计算出来,对于不同年龄的人,余年的概率分布不同。
第二步,确定每个余年值下的最优消费。为此,需要按每个余年值建立跨时效用函数和跨时预算约束条件,从中求解最优消费。
第三步,将第二步得出的每个余年值下的最优消费按第一步得出的余年概率加权求和,得出综合最优消费。
2.“预期余年法”。这种方法是用“预期余年”(余年的期望值)代替许多个可能的余年;个人每年在预期余年下建立跨时效用函数和跨时预算约束条件,从中求解最优消费。“预期余年”在人口统计学中有精确的定义和计算公式。
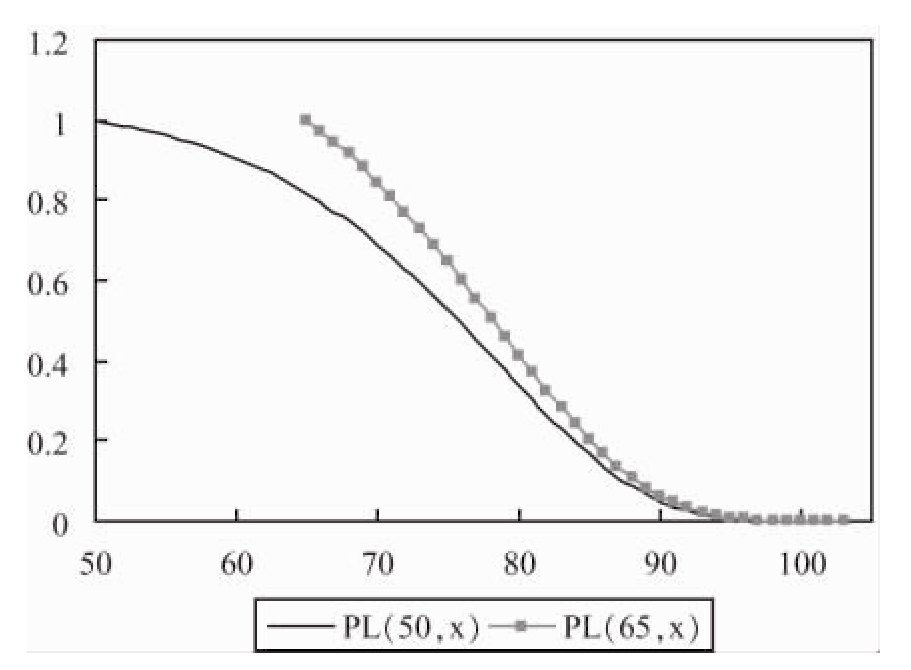
图1 50岁、65岁者到x岁还活着的概率(存活概率)
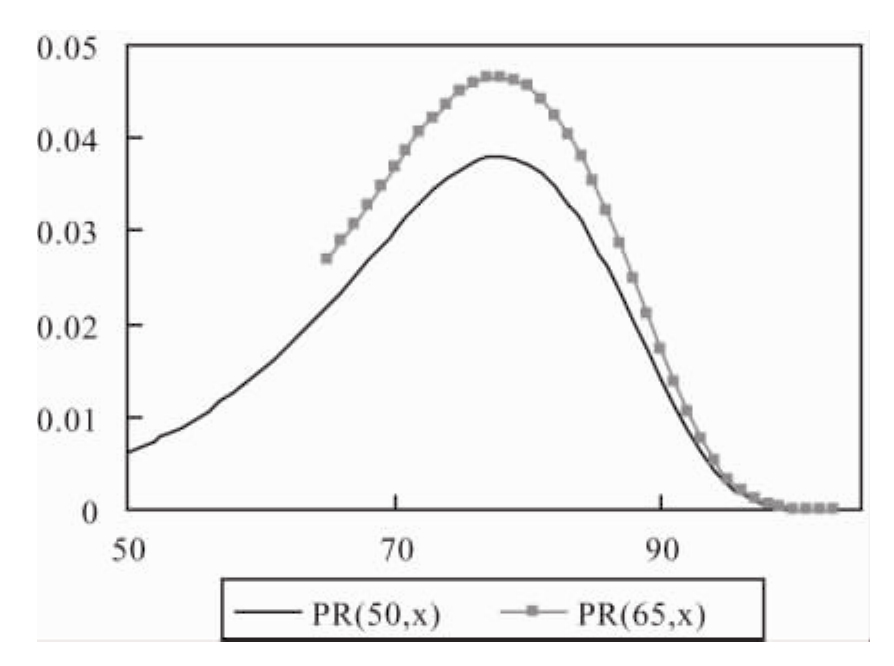
图2 50岁、65岁者死于x岁的概率(余年概率,曲线下的面积等于1)
比较这两种方法,从完美性说,方法1优于方法2;从简便性说,方法2优于方法1。
我们提出的这两种方法,与现有文献中所用的方法完全不同。对于现有文献中所用的方法,我们以布兰查德“永葆青春模型”中所用的方法为代表,给予批评。
(三)非预料死亡者的遗产如何处理
在不确定寿命模型中,如何处理非预料死亡者的遗产,是个难题。布兰查德提出的处理办法是:保险公司对活着的人支付保险金,在他们死亡时接收其全部财产;保险公司按自己收支相抵的原则确定统一的保险金支付率。我们提出的处理办法是:非预料死亡者的遗产由刚开始工作的人继承。有没有更好的办法,有待进一步的研究。
(四)人口的年龄结构
在确定的无限寿命中,人的年龄没有意义,因此不存在年龄结构问题。
在其他三种寿命假定中,人的年龄有意义,存在人口的年龄结构问题。当人口增长率为零时,人口按年龄的分布在确定的有限寿命下是均匀分布,在不确定的有限寿命下是半边宝塔形分布,在不确定的无限寿命下是负指数分布(见图3)。
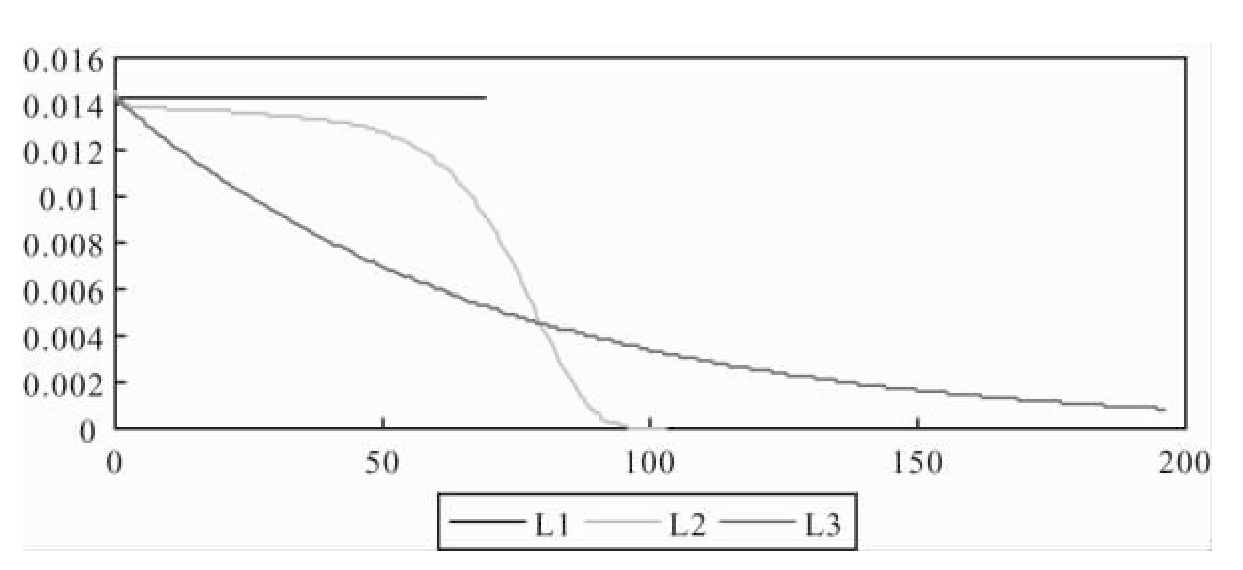
图3 不同寿命假定下人口的年龄结构
图中,水平线(L1)是确定的有限寿命下人口的年龄结构(假定每个人都活到70岁);半边宝塔形曲线(L2)是不确定有限寿命下人口的年龄结构(假定分年龄的人口死亡率等于中国1990年人口普查的死亡率表,平均寿命为68.5岁);负指数曲线(L3)是不确定无限寿命下人口的年龄结构(假定死亡概率为每年1/70,从而平均寿命为70岁)。
图3表明,不确定无限寿命和确定的有限寿命下人口的年龄结构都离实际较远。对于某些经济问题(如社会养老保险)的研究来说,这样的寿命假定是不合适的。
(五)工作期与退休期
在有限寿命中,个人生命有工作期与退休期的之分;而在无限寿命中,没有这种区分。对于消费问题的研究来说,这种区分很重要。因为在现实中,人们在工作期的收入一般高于退休期的收入;工作者与退休者人数比率、工作期与退休期时间比率、有无退休金、退休金的相对高低,对于社会储蓄率都有重要影响。所以,对于消费问题的研究来说,采用有限寿命比较好,无限寿命则不可取。
(六)有限寿命下的消费路径
在经济稳定增长(包括零增长)的条件下,按确定的有限寿命进行跨时优化,产生的个人消费路径是单调变化的,通常是单调增加,从而个人退休期的消费水平高于工作期的消费水平。其原因是:在合理设定参数的前提下,含确定的有限寿命的经济增长模型产生的资产收益率高于作为模型参数的时间偏好率,使得个人退休后消费高于退休前消费(见图4)。
不确定有限寿命的情况与此不同。在经济稳定增长(包括零增长)的条件下,按不确定有限寿命进行跨时优化,产生的个人消费路径不是单调变化的,而是表现为先上升后下降的形态,使得个人退休后消费低于退休前消费(见图5)。其原因是:不确定有限寿命下的消费路径,不仅与资产收益率与时间偏好率的对比有关,而且与余年的概率分布随年龄而改变有关。
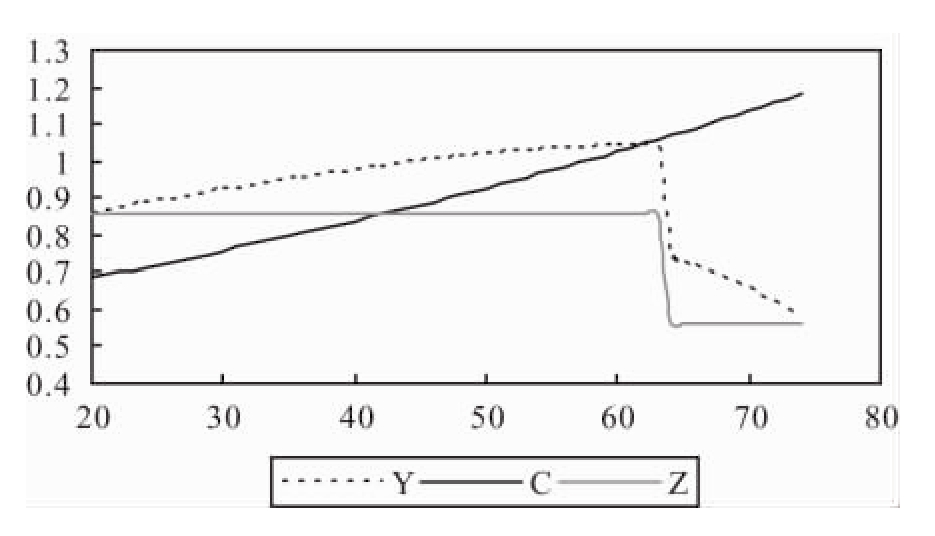
图4 工资零增长下,确定寿命的个人一生的收入(Y)、消费(C)、非资产收入(Z)
这两图哪一个比较符合实际?我们初步判断是图5比较符合实际。是否这样,读者可自己判断。如果我们的判断正确,那么,不确定有限寿命就比确定的有限寿命更可取。
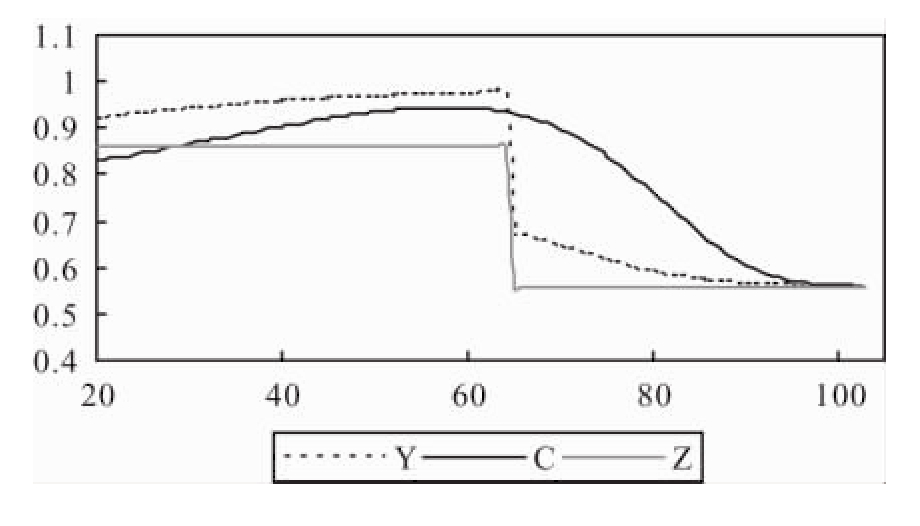
图5 工资零增长下,不确定寿命的个人一生的收入(Y)、消费(C)、非资产收入(Z)
(七)个人生命如何分期
在现有关于个人消费的有限寿命模型中,对个人生命的分期主要有两种:一种是分两期,分为青年期和老年期。如Diamond的世代交叠模型。另一种是按年分期。前者的优点是便于数学处理,可以得出模型的内生变量作为参数的函数的解析式。后者很难进行数学处理,得不出模型内生变量作为参数的函数的解析式;只能通过模型的数值模拟进行分析。
但是,分两期的模型存在严重缺陷。主要是:
(1)回避了收入预期问题。在两期模型中,个人工资收入只存在于生命的第一期,此工资收入对个人来说是已知数,因此个人消费决策不涉及工资预期问题。而在实际经济中,在职者的消费决策都涉及未来工资的预期问题;如何预期未来工资收入,对经济系统的动态有重要影响。
(2)人口的年龄结构和劳动者与退休者人数比率离实际太远。当人口增长率为零时,两期模型中的劳动者与退休者人数比率为1∶1;而在现实社会中,此比率一般大于3。
由于存在这些缺陷,两期模型得出的一些结论不符合实际。例如,在合理给定参数的条件下,Diamond的世代交叠模型得出“资产收益率变动对储蓄率的影响为负”。这与多数学者的实证研究结果不符。
Modigliani在关于生命周期消费的研究中,曾经把个人生命分为5期,前4期工作,后1期退休,也得出“资产收益率变动对储蓄率的影响为负”的结论。他说:“在一增长经济中,储蓄/总收入比率当利息上升时下降”。(见林少宫译,莫迪利亚尼文选,第175页,商务印书馆,1993年)。
按照同样的方法,我们把个人生命分为10期,前8期工作,后两期退休;或者个人生命按年分期,前44年工作,后11年退休,却得出相反的结论:“资产收益率变动对储蓄率的影响为正”。
这些说明:对于某些问题的研究,个人生命分期数不能太少,否则会得出不正确的结论。
(八)未成年人的消费如何处理
关于未成年人的消费,现有模型一般笼统地假定由成年人供给,但在成年人的跨时效用函数和跨时预算中不具体地表现出来。因此在模型中根本不纳入未成年人。如果要在成年人的消费决策中考虑未成年人的消费,模型就太复杂了,而且很难准确描述。因为不同年龄的成年人的负担不同。
一种可考虑的解决办法是:把未成年人的消费作为一种负担纳入成年人的跨时预算中,但不纳入成年人的跨时效用函数中。为了测试这种办法,我们构建了一个个人生命分为4期(未成年期、青年期、中年期、老年期)的经济增长模型。其中未成年人的消费作为负担纳入青年人和中年人的跨时预算中。模型得出的结论与个人生命分为3期(青年期、中年期、老年期)的模型得出的结论没有质的区别。
二、关于未来收入的预期
在消费的跨时优化的多期模型中,必然涉及对未来收入的预期问题,而且预期涉及的时间很长。例如,对于一个20岁的人来说,如果他打算工作到64岁,预期能活到80岁,那么,他就要对未来44年的工资收入和以后16年的退休金做出预期,才能对现在(20岁)的消费做出优化决策。显然,对如此长时期的收入做出正确的预期是不可能的,做出比较正确的预期也是很困难的。在现有文献中,关于未来收入的预期主要有以下两种假定:
一种是理性预期。在确定性模型中,理性预期者假定人们对未来的收入完全预知(perfect-foresight);在随机性模型中,理性预期者认为人们对未来的收入虽然不能完全预知,但能够做出无偏预期。
另一种是“幼稚预期”。在确定性模型中,它以当时的收入水平预期未来长时期的收入水平;在随机性模型中,它以当时的正常收入水平预期未来长时期的收入水平。Modigliani在他的题为“效用分析与总量消费函数:统一的释义”的文章中,采用的就是这样的预期(见林少宫译《莫迪利亚尼文选》第四部分,商务印书馆,1993年)。
在稳定的经济增长模型中,理性预期表现为无偏的趋势预期;“幼稚预期”表现为有偏的水平预期(如图6所示)。
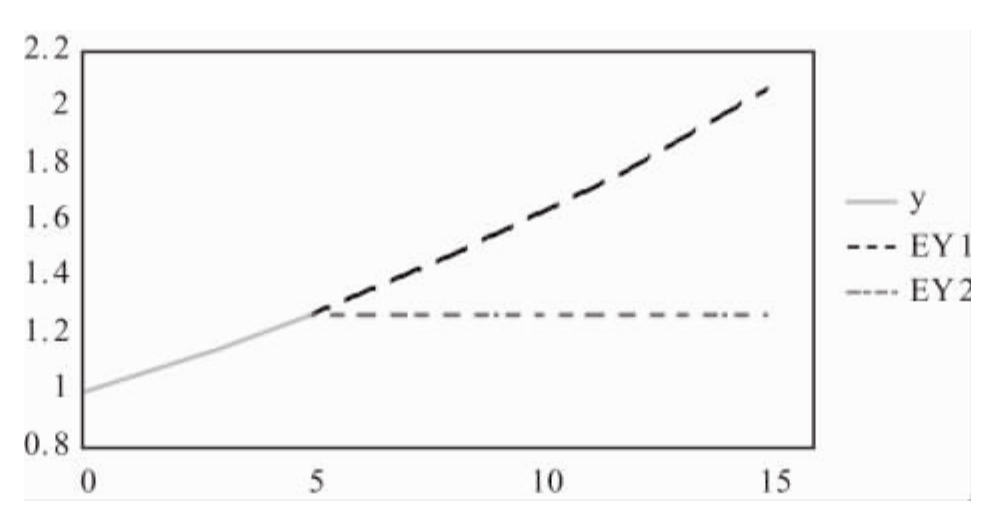
图6 对未来收入的趋势预期与水平预期
图6中,实线表示收入在最近一段时期(时期0到时期5)的实际变动;往上延伸的虚线表示在时期5对未来收入的趋势预期;水平延伸的虚线表示在时期5对未来收入的水平预期。
这两种预期哪种比较符合人们的实际行为,很难直接判定,需要根据与其相联系的模型的分析结果与实际对照才能判定。我们把这两种预期交替纳入带生命周期消费的新古典增长模型,用该模型研究经济增长率和资产收益率变动对储蓄率的影响,得到如下结论:
当对未来收入的预期采取水平预期时,经济增长率变动对储蓄率有较大的正影响,资产收益率变动对储蓄率有较小的正影响;当对未来收入的预期采取趋势预期时,经济增长率变动对储蓄率的影响为负,资产收益率变动对储蓄率有较大的正影响。
查阅前人的实证研究,大多数学者的结论是:经济增长率变动对储蓄率有较大的正影响;资产收益率变动对储蓄率有较小的正影响。与上面的结论对照,可知:对未来收入的水平预期比较符合实际,对未来收入的趋势预不符合实际。
三、主要结论
总结本文的分析,有以下主要结论:
1.经济模型关于个人寿命的假定与人口的年龄结构有内在的联系。不确定的有限寿命所对应的人口年龄结构最接近实际,最适宜于社会养老保险、人口变动对经济的影响等问题的研究。
2.在不确定寿命下,人的余年(还能活多长时间)是随机变量。其概率分布可根据人口死亡率表计算出来。我们以余年概率分布为基础,提出了不确定寿命下个人消费决策的两种方法—余年分析法和预期余年法。它们比前人以存活概率为基础的分析方法更正确、更科学。
3.在有限寿命中,个人生命有工作期与退休期之分,人们在工作期的收入一般高于退休期的收入,工作者与退休者人数比率、工作期与退休期时间比率、有无退休金、退休金的相对高低,对于社会储蓄率都有重要影响。所以,对于消费问题的研究来说,采用有限寿命比较好,无限寿命因没有工作期与退休期之分而不可取。
4.我们把对未来收入的两种预期预期方式(趋势预期和水平预期)交替纳入带生命周期消费的新古典增长模型,用以研究经济增长率和资产收益率变动对储蓄率的影响,发现:对未来收入的水平预期比较符合实际,对未来收入的趋势预不符合实际。这实际上否定了“理性预期”在长期收入预期上的现实性。
[参考文献]
1.Diamond,P.A.,1965,“National Debt in a Neoclassical Growth Model”,The American Economic Review,vol.LV,No.5,PART 1,pp.1126-1150
2.Miller,H.M.and Upton,W.C.,1974,Macroeconomics,a Neoclassical Introduction,Section Two,pp.73-144,The University of Chicago Press
3.Hurd,Michael D.,1989,“Mortality Risk and Bequests”,Econometrica,Vol 57,n4,pp.779-813
4.布兰查德、费希尔:《宏观经济学》中的“永葆青春模型”,经济科学出版社1992年版,第124~133页
5.罗默:《高级宏观经济学》,商务印书馆1999年版,第52~116,第118~247页
6.贺菊煌:《寿命不确定下的消费决策》,《数量经济技术经济研究》2004年第12期
7.贺菊煌:《带生命周期消费的经济动态模型》,《吉林大学社会科学学报》2004年第3期
8.贺菊煌:《储蓄率:基于寿命不确定模型的分析》,载汪同三、陈收主编:《21世纪数量经济学》第4卷,湖南大学出版社2004年版,第71~90页
9.贺菊煌:《人口变动对经济的影响》,《数量经济技术经济研究》2003年第12期;《人口与经济》2004年第2期
10.贺菊煌:《消费函数分析》,社会科学文献出版社2000年版
(原载《经济研究》2005年第8期)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。














