投入产出表转移矩阵的数学调整法

投入产出表转移矩阵的数学调整法——拉格朗日未定系数法

龚飞鸿　杨树庄　李　杰

一、问题的提出与模型

产业层次生产率研究中，我们使用了生产者行为模型，它是生产的一般均衡模型，即静态投入产出表。为了测定产业部门生产率，必须具有时间序列的投入产出表。我们在生成1981～1987年系列投入产出表时，基于我国已调整且具有可比性的1981年、1983年和1987年的三张投入产出表，应用了日本庆应大学黑田教授在20世纪80年代首先提出的拉格朗日未定系数法。

自1962年斯通提出RAS法调整投入产出关系中的转移矩阵以来，数学方法的探索深入该解的存在性、唯一性和迭代的收敛性等问题。哥曼、毕金和巴恰切等的研究成果，在一定的约束条件下，回答了这些问题，但RAS法存在着固有的困扰，诸如超大矩阵约束条件的检验，以及原始矩阵和给定边际约束的微小变动引起迭代结果的不稳定性。日本黑田教授提出对非负矩阵及约束，在加权二次目标函数取极小时的估计方法，因为方法中引入拉格朗日未定乘数，故此法称为拉格朗日未定系数法。

在上述条件下，寻求估计转移矩阵(x_ij)(1，2，…，m，j=1，2，…，n)且满足约束:

以上提出的问题，它具有m+n个约束，有m×n个变量，除了m= n=2的特殊情形下，此问题有无数解(x_ij)，不能确定唯一解。考虑到投入产出关系中，技术系数在短时间内具有相对稳定的特点，引入估计期与基期技术系数相对差平方和最小为目标函数，求(x_ij)的唯一解。

定义:c_ij=xo_ij/zo_i，称基期转移矩阵的列系数;

ij=xo_ij/yo_i，称基期转移矩阵的行系数。

则目标函数和约束条件为:

约束于:

由上述，我们可以认为估计x_ij，像一个目标函数和约束方程(5)和(7)的误差极小的问题。即:

式中λ(i=1，2，…，m)和δ(i=1，2，…，n－1)是拉格朗日乘数。则v(x_ij，λ_i，δ_j)存在的充分条件是:

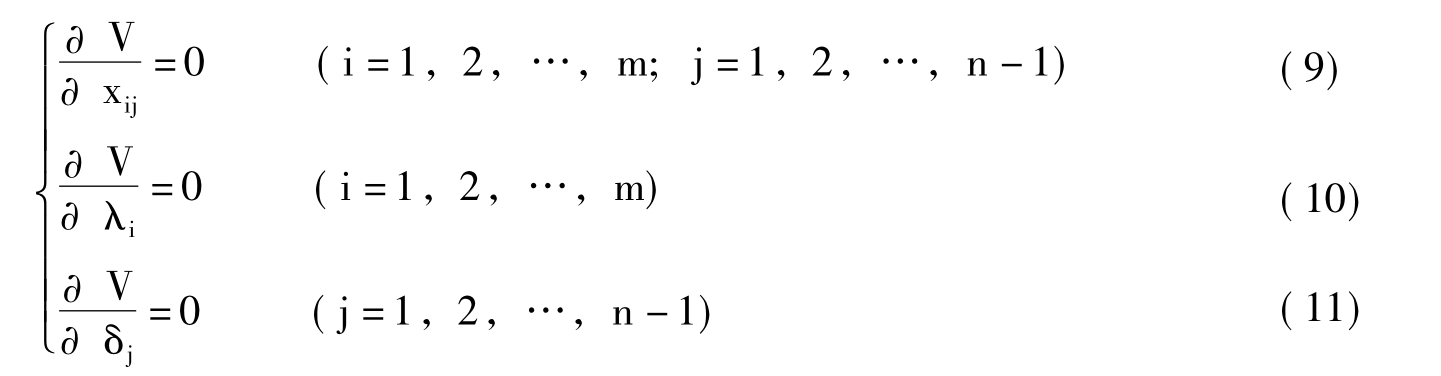
二、求解方法

由(9)得:

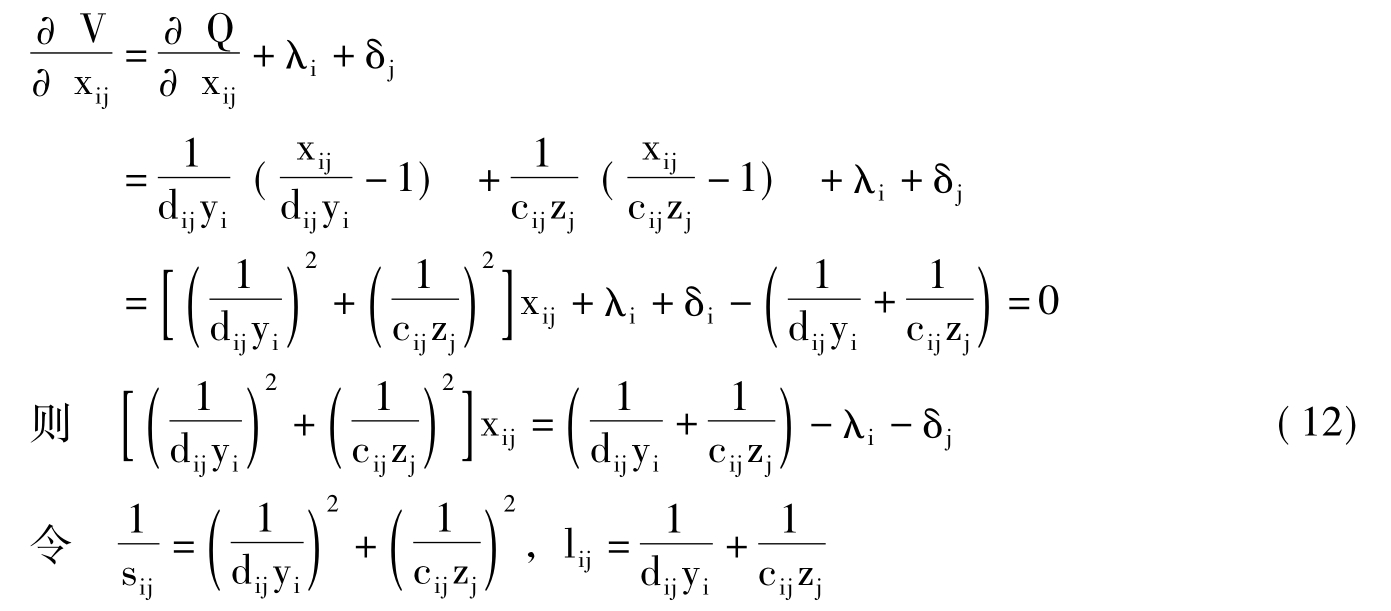
(12)式简写为

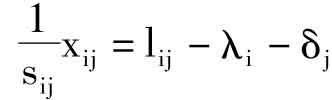
所以

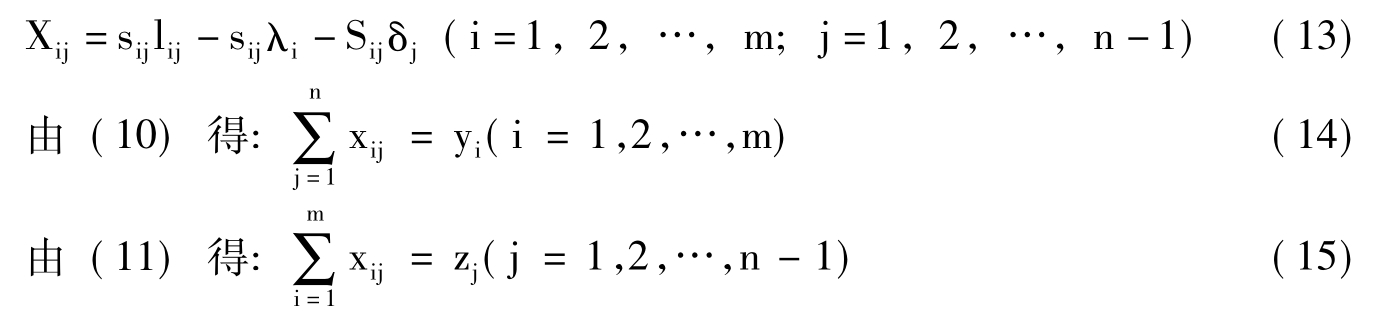
将(13)式分别代入(14)及(15)式得联立方程组:

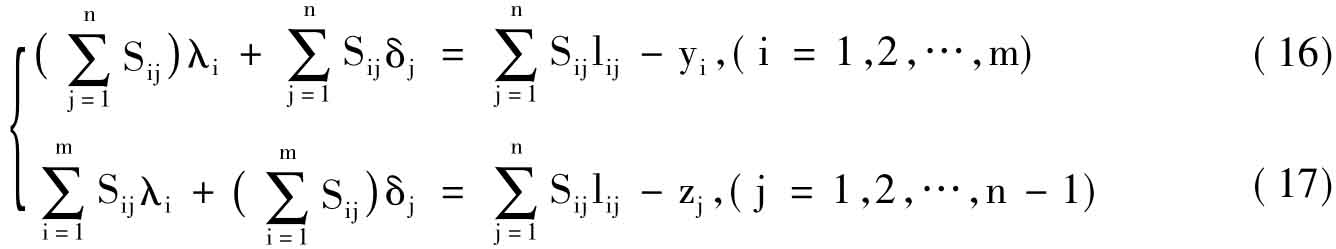
它具有λ₁，λ₂，…，λ_m，δ₁，δ₂，…，δ_n－1等m+n－1个变量，并有m+n－1个，它的矩阵形式是:

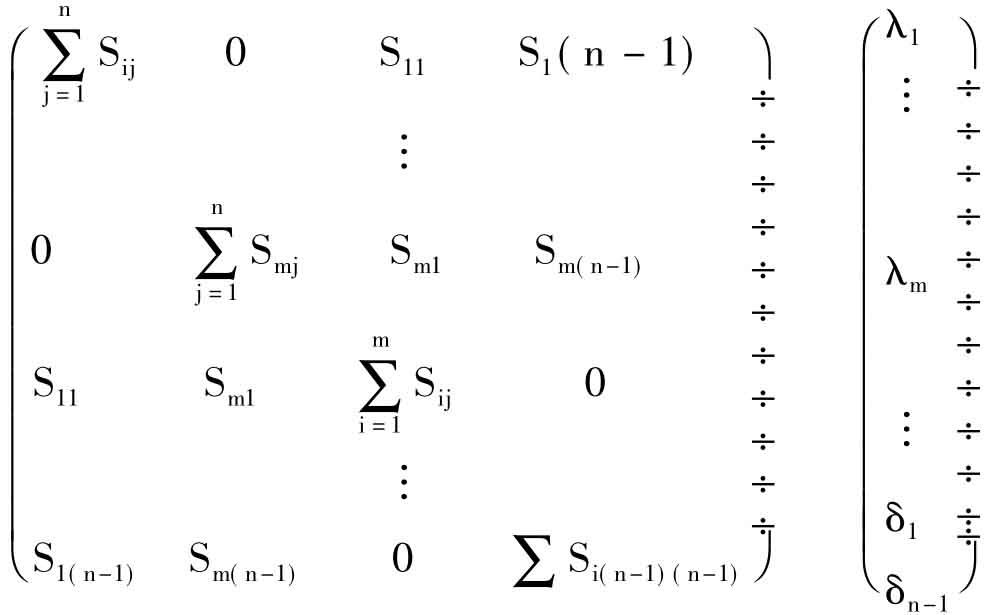
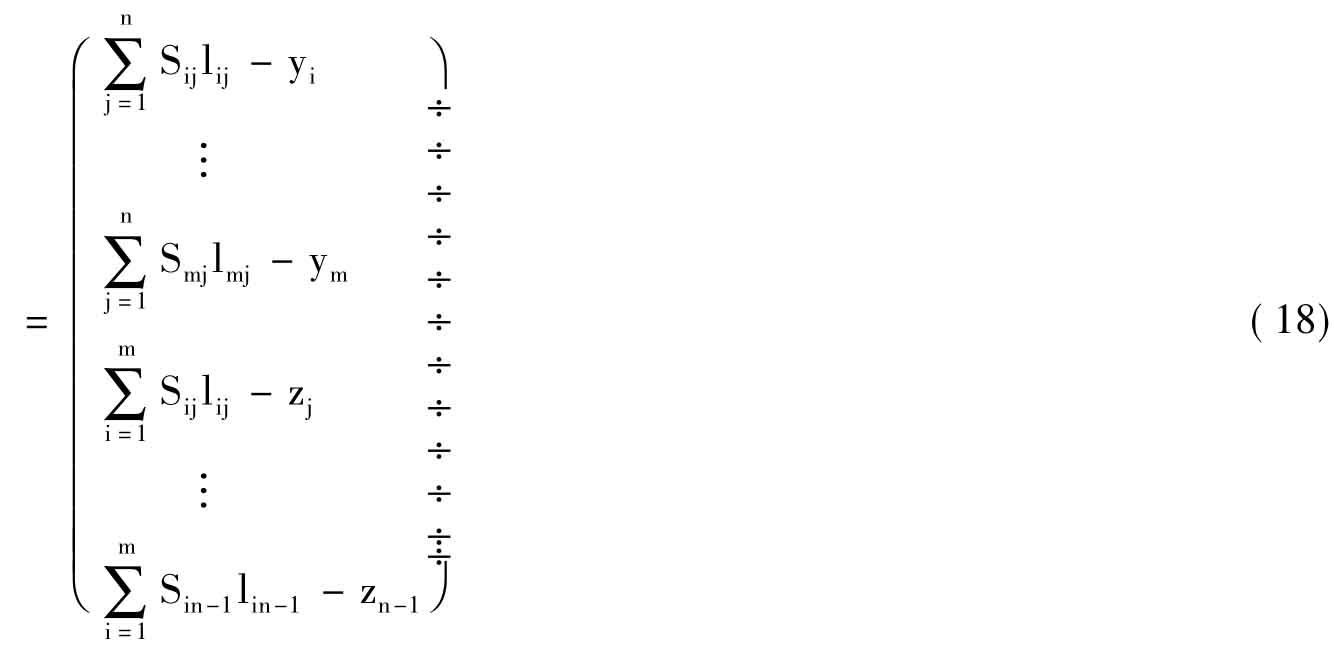
从投入表转移矩阵的构成特性，在剔除了矩阵中全零元素的行(或列)以后，由它生成的方程组(18)，每一个方程都是独立的，所以其系数矩阵是满秩，方程(18)有唯一解。故而(13)式被确定，x_ij(i=1，2，…，m;j=1，2，…，n－1)是唯一的。x_ij的最后一列元素x_in是:

也是唯一的。当m和n很大时，可将(18)式矩阵分块为:

式中:

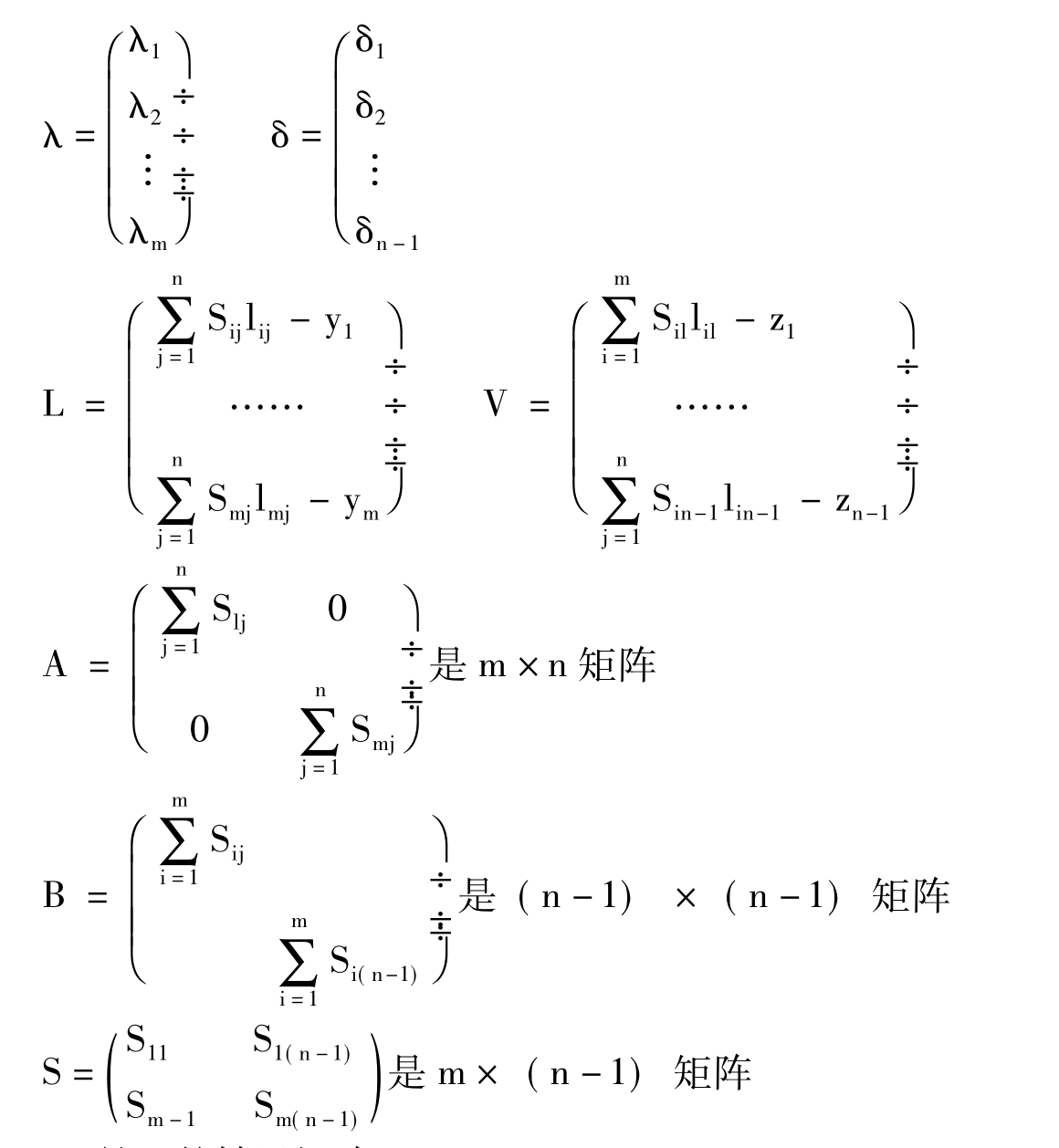
TS是S的转置矩阵。

将(20)写成联立方程是:

则其解为:

再代入(13)、(19)求出(x_ij)m×n。

三、案例

设基期基本流量矩阵为:

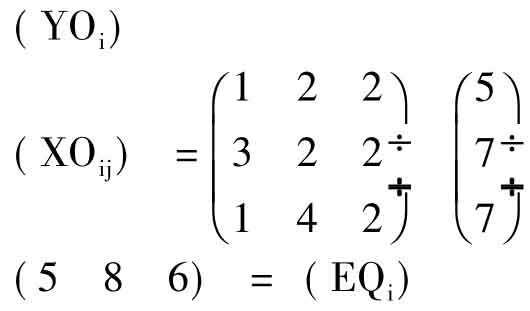
求解步骤如下:

1.先求出基期转移矩阵并yo_i、zo_i的(c_ij)和(d_ij)，得:

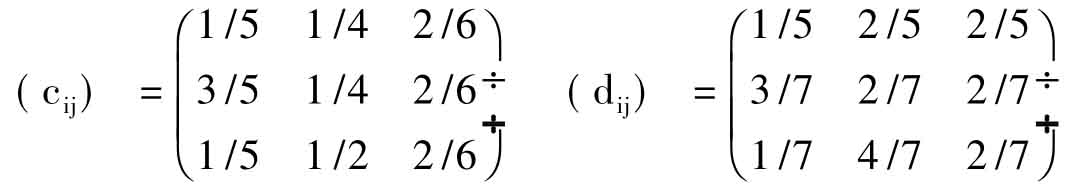
2.根据假设求出(x)，(l)_i^j_ij及S_ijl_ij得:

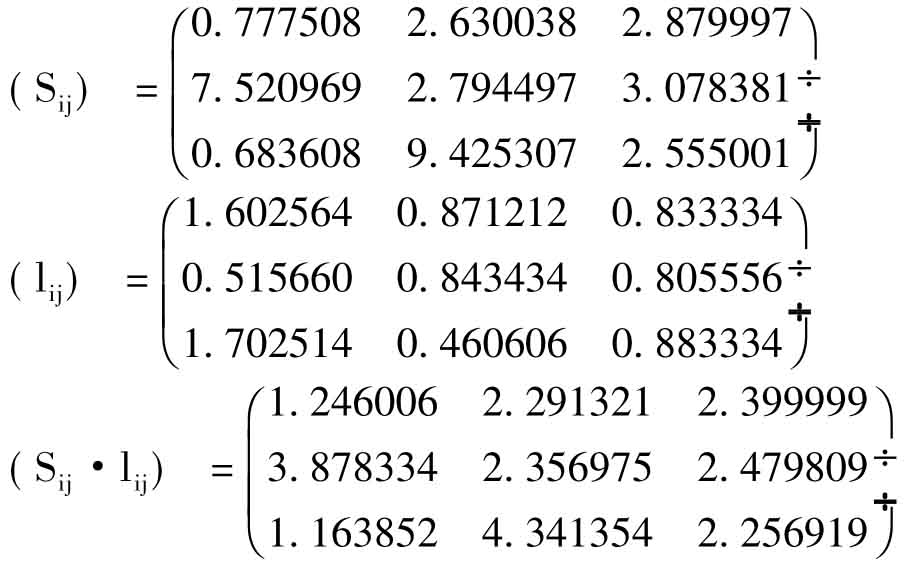
3.引入拉格朗日未定乘数后的方程组是:

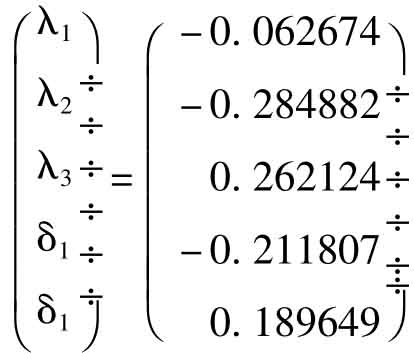
求解后得:

4.新的基本流量矩阵(S_ij)

(原载李京文等著:《生产率与中美日经济增长研究》，中国社会科学出版社1993年版。这次做了压缩和微小改动)