阿拉伯人的数学和天文学贡献

除了翻译和保存，阿拉伯人也做出了不少独创性的科学成就。

首先必须提到马蒙的宫廷数学家花拉子米（约公元780年—850年），他整理了印度数学，引入包括0在内的印度数字，引入了小数、分数和负数等。他的另一部著作《还原和化简的科学》更是影响深远，其中还原（al-jabr） 译成拉丁文就成了今天的代数（algebra） 一词。虽然更早的亚历山大城的丢番图就被誉为代数之父，但花拉子米对欧洲科学的影响更加直接。

不过其实花拉子米的这本书并不含有方程和代数符号，即便是他自己引入的印度数字符号也很少使用，而是充斥着几何图形及其描述（图5.5.1），实质是用欧几里得几何学来解决我们现在所谓的代数问题（解方程）。

比如说我们要解形如x2+bx=c的一元二次方程，花拉子米给出的一个方法如下（图5.5.2） ：

求解x2+10x=39，作一个边长为x的正方形，然后从两个方向分别延长出10/2，也就是5，就形成了两个面积为5x的矩形，合起来就是10x，此时x2+10x就是那一个正方形和两个矩形的面积，然后我们发现再补上一个边长为5的正方形，就又构成了一个边长为（x+5）的大正方形。那么这个大正方形的面积应该是（39+5×5），也就是64，算出来边长是8，所以就解出来x+5=8，x=3。当然我们现在知道这个方程还有一个负根是-13，但花拉子米从几何学的视角看来没有意义。

图5.5.1　花拉子米《代数学》中的一页

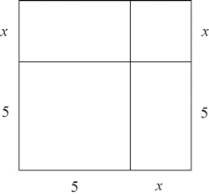
图5.5.2　花拉子米解题图形

阿拉伯人在天文学方面也成果斐然。一方面阿拉伯人吸收了托勒密的《天文学大成》并赞誉其“伟大之至”，但另一方面并未就此止步。他们承认托勒密体系的思路和技巧，但对其具体的模型和数据保留意见。阿拉伯人一方面通过天文观测校正托勒密模型的参数，另一方面也在不断改进新的行星模型，并且试图化解托勒密体系与亚里士多德物理学的冲突。

例如，在13世纪的马拉盖学派（马拉盖位于伊朗北部，当时阿拉伯世界最大的天文台之一坐落于此） 发展出一套几何工具，称为图西双轮（Tusi couple）（图5.5.3），用两个圆的运动合成出一个往复的直线运动。稍后，14世纪的伊本·沙提尔借助图西双轮，建立出一套不再需要托勒密“匀速点”的行星模型（图5.5.4）。这一模型虽然仍是地心体系，但在数学上基本与哥白尼体系等价。科学史家没有找到哥白尼引用马拉盖学派的证据，但很少有人会认为这只是单纯的巧合。有科学史家评论道：“问题不是哥白尼是否了解马拉盖理论，而是何时、何地和以何种形式了解了马拉盖理论。”^[8]

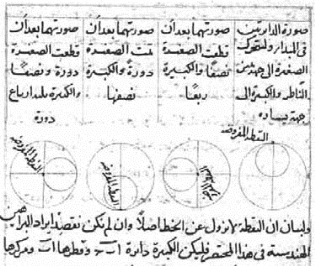
图5.5.3　13世纪抄本中描绘的“图西双轮”

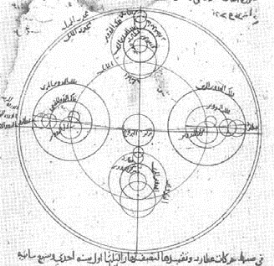
图5.5.4　伊本·沙提尔的水星模型

在天文观测方面，阿拉伯人建立了许多专业的天文台，包括一个带有观测孔的穹顶，一座配套的图书馆，还有精密的观测仪器和大量专职天文学家。例如在撒马尔罕的天文台配有半径40米的巨型六分仪（图5.5.5），用以确定天体穿过子午线时的纬度。

图5.5.5　撒马尔罕天文台的巨型六分仪

阿拉伯人还发明或改良了星盘（图5.5.6），这是一项在天文学、地理学、航海和占星等领域用途广泛的观测工具。

阿拉伯天文学如此发达，以至于中国从元朝起专设回回司天监，引入阿拉伯天文学。明朝的钦天监仍然沿用元制，分别处理汉历和回回历，并引入阿拉伯人的数理方法，明朝的贝琳依据阿拉伯天文学编著出《七政推步》，推算日、月和五大行星，但托勒密体系的几何模型在中国基本上都被置换为代数方法。

阿拉伯天文学的繁荣也许与其宗教需求有一定关系，伊斯兰教要求在确定的时刻进行某些仪式，因此需要精确的时间和历法测量。另外伊斯兰教有朝向麦加进行朝拜的仪式，而在世界各地确定麦加的方位就成了一个重要课题。

图5.5.6　阿拉伯星盘（1067年）