天文推算的代数方法

当然中国古代天文学不光擅长观测，推算方面也不弱。在历法方面，主要问题是计算年、月、日的关系，古代中国人很早就有了非常精确的数据，对月食的周期也有准确的认识。至于日、月和五大行星的运行，包括其不均匀性，中国古人虽然没有建立几何模型来进行解释，但是基于经验记录和代数方法，也能够得到相对准确的估测。

在商代的卜辞中就记录了详细的天象观测，例如可能记录了一次冬至后经过548天回到夏至，这似乎是试图通过更长跨度的记录来推定回归年的精确数值。至少在汉代，中国人就已经很明确一个回归年大概有365.25天，一个朔望月大约有29.53天，随着中国天文学的发展这些数值也在不断趋于精确。^[6]

至于日、月和五大行星的不均匀运动，中国古代是通过代数方法估算的，例如在唐初李淳风的著作中就引入了二次方程和有限差分法来处理太阳运动的不均匀性，下面我用现代的符号简单解释一下这种方法：

通过观测数据可以得知太阳在不同的时间间隔t所移动的角度x，现在要求出x和t的关系。于是我们假定 x=at2+bt，其中a、b为常数。然后代入观测所得的数据，如 x1=at12+bt1；x2=at22+bt2……

然后两两相减，得到：

类似有

再两两相减，得到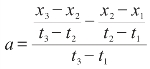，这就得到了a和b的数值解。^[7]

郭守敬在1281年把这一方法推广到更高次，欧洲人在17、18世纪才掌握类似的方法。

利用代数方法，中国人也可以较精确地预测日食、月食的发生，然而正如第四讲提到的，与希腊天文学不同，中国天文学家不使用几何模型，天文预测与宇宙论图景并无关系。

中国从元朝起专设回回司天监，引入阿拉伯天文学——也就是托勒密体系。明朝的钦天监仍然沿用元制，分别处理汉历和回回历，并引入阿拉伯人的数理方法，明朝的贝琳依据阿拉伯天文学编著出《七政推步》，推算日、月和五大行星，但托勒密体系的几何模型在中国也被置换为代数方法。