广义相对论

到这里，相对论只处理了惯性系的问题，但还没有处理非惯性系，也就是加速运动方面的问题。同时，光速不变的设定还没有考虑引力的问题，因为在牛顿力学中引力被认为是一种瞬时的超距作用，但如果存在这种瞬时传播的信号的话，那么之前谈到的测量的相对性就瓦解了。

因此爱因斯坦接下来的任务就有两项，也就是把加速运动和引力纳入相对论之中。

爱因斯坦在1907年就做出了一个重大突破^[5]，这个突破仍然源于一次思想实验（图15.5.1）。他设想一个人位于密封舱中，这个人感受到向下的重力，但无法判断这种重力是因为密封舱静止在一颗行星的地面而受到引力，还是因为密封舱在星际空间中加速推进。于是，加速运动仍然不是一种绝对的运动。

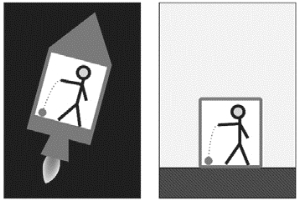
图15.5.1　广义相对论的思想实验

图15.5.2　爱因斯坦在1921年

这一思想实验包含一个推论，那就是光线会在引力场中弯曲，因为在密封舱外面观察一束横穿密封舱的光线，如果这条光线对于舱外的观察者而言是直线，那么它在密封舱内的轨迹将是曲线，因为光从舱内一端穿到另一端的同时密封舱在加速上升。

如果说舱内观察者无法区分加速运动和引力的话，那么他们在受到引力的情况下也应该能够看到弯曲的光线，否则的话他在观察到弯曲的光线时就可以断定自己绝对处在加速运动之中了。

光线在引力场中弯曲的现象在1919年日全食时的一次观测中被爱丁顿验证，从而让爱因斯坦声名鹊起。但这一次著名的验证的意义被高估了，根据对观测记录的还原，科学史家发现当时这场观测对误差的处理是有问题的，实际的证明力非常有限。另一方面，事实上牛顿把光看作粒子流的理论也能够预言光的弯曲，只是在弯曲程度上与爱因斯坦的估计有差异。

爱因斯坦本人也并不关心这一观测验证，他的态度和伽利略类似：既然已经由思想实验得到了必定如此的结论，又何须在乎实际验证呢？

当我们说光线“弯曲”的时候，我们还要继续贯彻测量的相对性原则：究竟什么是弯，什么是直呢？曲和直难道不也是测量——也就是与某种相对之物进行比较——的结果吗？木匠用直尺来测量曲直，但直尺的“直”又是由其他直尺所度量的，曲直的测量仍然是相对的。那么有没有一把绝对准确的直尺来提供绝对的曲直的裁定呢？如果说最准确的直尺，那就莫过于光线了，最精密的工匠就是用光线来裁定曲直的。但如果说光线也会弯曲那意味着什么？

如果我们坚持测量的相对性和“光”的绝对性，那么就可以有这样的结论：光仍然在走直线，因为“直”这一量度本来就是光线说了算嘛。也就是说，光总是走两点之间最近的距离。当然这种直线不再是欧氏几何中的了，而是非欧几何中的“直线”。

想到这里，爱因斯坦在1912年找到他的老同学格罗斯曼求助，当年爱因斯坦在苏黎世工学院上学的时候经常逃数学课，多亏了格罗斯曼借他笔记。

格罗斯曼的博士论文就是关于非欧几何的。在格罗斯曼的启发下，爱因斯坦借助黎曼几何发展广义相对论。到1915年，他开始与希尔伯特交流，之后一方面受到这位大数学家的帮助，另一方面也受到竞争的压力——因为希尔伯特也想亲自试试完成这个数学体系的建构。总之最后在1915年年底，爱因斯坦和希尔伯特差不多同时给出了广义相对论最终的数学方程。

当然，提出广义相对论的荣誉毫无疑问还是属于爱因斯坦的，爱因斯坦的确不太擅长数学，但整个理论的构想无疑是他独立完成的。希尔伯特本人也对爱因斯坦的物理学直觉大为赞赏，据说他曾经说道：“关于四维几何，哥廷根大街上的每一个孩子都比爱因斯坦知道更多……然而尽管如此，做出这项工作的是爱因斯坦，而不是数学家们。”^[6]

广义相对论把引力解释为空间弯曲，于是月球绕着地球转可以理解为在一个黎曼空间内仍然在走“直线”。这种非欧几何的空间论貌似又把作为背景的“绝对空间”引回来了，但实际不然，在某种意义上广义相对论是向亚里士多德式的空间概念的回归，那就是说：不能脱离具体的物体来谈空间。

图15.5.3　在广义相对论下，地球的卫星其实是在“直线”上运动