网络结构和学习算法

一、SOM网络结构和学习算法

SOM网络由输入层和竞争层组成，其网络基本结构如图3.11所示。

图3.11　SOM网络结构图

输入层各神经元通过权向量将外界信息汇集到竞争层的各神经元，其形式与BP网络相同。竞争层的排列有多种形式，如一维线阵、二维平面阵，也可以推广到多维阵列中去。SOM网络的一个典型特征就是可以在一维或二维的阵列上，形成输入信号的特征拓扑分布。因此，SOM网络具有抽取输入信号模式特征的能力。

SOM网络的基本思想是网络竞争层中的各神经元通过竞争来获取对输入模式的响应机会。它采用Kohonen算法，是在胜者为王算法基础上加以改进而成的，其主要区别在于调整权向量与侧抑制的方式不同。SOM网的获胜神经元对其邻近神经元的影响是由近及远，由兴奋逐渐转变为抑制。因此，其学习算法中不仅获胜神经元本身要调整权向量，它周围的神经元在其影响下也要程度不同地调整权向量。以获胜神经元为中心设定一个邻域半径，该半径圈定的范围就是优胜邻域。在SOM网学习算法中，优胜邻域内的所有神经元均按其离开获胜神经元的距离远近不同程度地调整权值。优胜邻域开始定得很大，但其大小随着训练次数的增加不断收缩，最终收缩到半径为零。其运行过程为:

第一步，初始化。假设网络输入为X，输出神经元i与输入单元的连接权值为W_i。对N个输入神经元到输出神经元的连接权值赋予较小的权值。选取输出神经元j个“邻接神经元”的集合s_j。

第二步，提供新的输入模式X。

第三步，计算欧氏距离d_j，即输入样本与每个输出神经元j之间的距离:

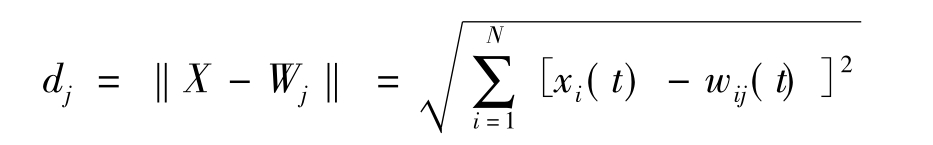
并计算出一个具有最小距离的神经元j^*，即确定出某个单元k，使得对于任意的j，都有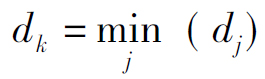

第四步，给出一个周围的邻域s_k(t)。

第五步，按照下式修正输出神经元j^*及其“邻接神经元”的权值:

w_ij(t+1)=w_ij(t)+η(t)［x_i(t)－w_ij(t)］

其中，η为一个增益项，并随时间变化逐渐下降到零，一般取

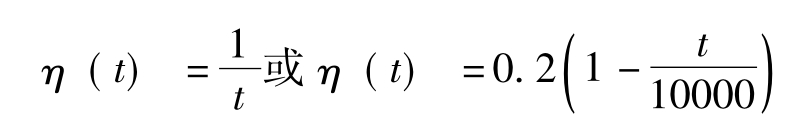
第六步，计算输出o_k:

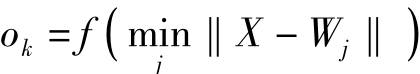
其中，f(.)一般为0－1函数或其他非线性函数。

第七步，提供新的学习样本重复上述学习过程。