由参数α，β生成的模糊粗糙集的粗糙度度量补充

由参数α，β生成的模糊粗糙集的粗糙度度量补充

四川广播电视大学　吴润民

【摘　要】　模糊粗糙集的粗糙度度量是根据粗糙集理论和模糊集理论而构建的一种新的度量方法。该方法能较好地发挥粗糙集理论和模糊集理论的长处，克服了两者的不足。本文结合集合间的相互关系及集合的运算规律，对M.Banerjee,S.K.Pal等构建的由参数α，β生成的模糊粗糙集的粗糙度度量方法[2]具有的性质和定理进行补充，并对补充的性质和定理给出了证明。

【关键词】　参数α，β；模糊粗糙集；粗糙度

如何在信息不完全、不精确或模糊的情况下，根据已有的数据挖掘潜在的、有利用价值的信息已成为学术界面临的一大难题。因此，作为有效解决此类问题的两大理论基础，由波兰数学家Pawlak提出的粗糙集理论和美国著名控制论专家Zadeh提出的模糊集理论[1] ，近年来得到了较为迅速的发展。粗糙集是通过集合关于已知可利用信息的一对上、下近似来描述不确定性概念，而模糊集则是通过对象关于集合的隶属程度来近似描述，这两种理论有着很强的互补性。但两者都存在着不足，粗糙集理论没有给出如何用已知的知识粒来精确或近似地描述边界不确定的目标集合X的方法。模糊集理论的隶属程度给出的大多是由专家凭经验给出的，存在着较大的主观性。因此，如何有效的结合两种理论，克服各自缺陷，给出更为有效的描述方法成为研究的重点。本文结合集合间的相互关系及集合的运算规律，对M.Banerjee,S.K.Pal等构建的由参数　,αβ生成的模糊粗糙集的粗糙度度量方法[2]具有的性质和定理进行补充，并对补充的性质和定理给出了证明。

定义　1[3]　给定信息表知识表达系统，对于任一对象集合X　U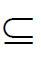　和属性集合，X关于R的上近似集和下近似集分别定义如下：是不分明关系R在U上的划分。集合称为X的R正域，称为X的R边界域。

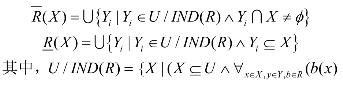
定义2[4]　设，若对，，则称关系R是自反的。

下面从设定相关参数的角度定义粗糙度，并验证了粗糙度具有的相关性质。

定义3[2]　设U是非空有限论域，R是U上的模糊自反关系，A∈F(U)，则A在近似空间(U,R)下依参数0＜β≤α≤1的下近似和上近似分别为：

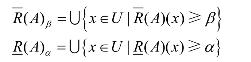
性质1　设U是非空有限论域，R是U上的模糊自反关系，　A,B∈F(U)，则对于0＜β≤α≤1有

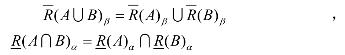
性质2　设U是非空有限论域，R是U上的模糊自反关系，　A,B∈F(U)，则对于0＜β≤α≤1有

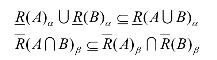
性质3　设U是非空有限论域，R是U上的模糊自反关系，　A,B∈F(U)，则对于0＜β≤α≤1有

若A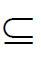B，则

性质4　设U是非空有限论域，R是U上的模糊自反关系，　A,B∈F(U)，且A≈B，则对于0＜β≤α≤1有

证明：由A B≈有

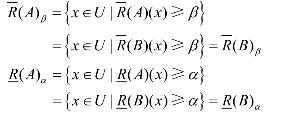
性质5　设U是非空有限论域，R是U上的模糊自反关系，　A,B∈F(U)，则对于0＜β≤α≤1有

性质6　设U是非空有限论域，R是U上的模糊自反关系，　A,B∈F(U)，则对于0＜β≤ α≤1有

推论1设U是非空有限论域，R是U上的模糊自反关系，A,B∈F(U)，则对于0＜β≤α≤1有

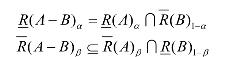
证明 因为　A−B= A∩～B ，根据性质1及性质6则有

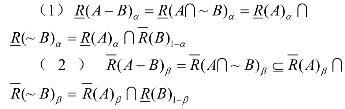
定理1　设1R和2R为论域U上的两个模糊自反关系，若

证明：

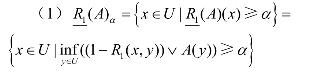
由R1　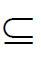R2有R1(x,y)　≤　R2(x,y)，则

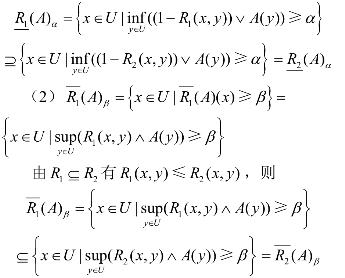
定理2 设1R和2R为论域U上的两个模糊自反关系，　A∈F(U)则有

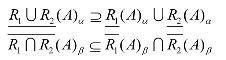
证明：

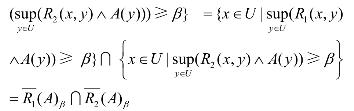
定义4　[2] 设U 是非空有限论域， R 是U 上的模糊自反关系，A∈F(U)，定义A在近似空间(U,R)下依参数α ,β ，0＜β ≤α ≤1的粗糙度

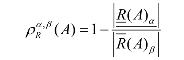
通过对参数的假设，由定义可得如下性质：

（2）若1R和2R为U上的两个模糊自反关系，

（ 3 ） 若A∈P(U) ， 且对关系R 恒有

证明：

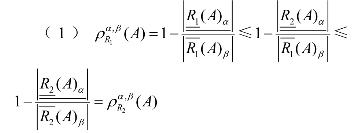
（2）由A 是U 上的经典子集，则对任意x∈U ， A(x) = 0或A(x) =1。由定义可知，此时上近似

由

定理3设U 是非空有限论域，是U 上的模糊自反关系，A, B∈ F(U)，且A 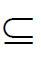B，0＜β ≤α ≤1，则

（2）由A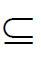B有 R(A)β 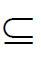R(B)β 。又已知则有

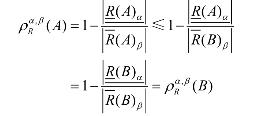
推论2　设U 是非空有限论域， R 是U 上的模糊自反关系， A, B∈ F(U)，若A ≈ B ，则对任意α ,β 满足0＜β ≤α ≤1有

定理4设U 是非空有限论域，R 是U 上的模糊自反关系， A, B∈ F(U) ， 参数α ,β 满足0＜β≤α≤1，则有

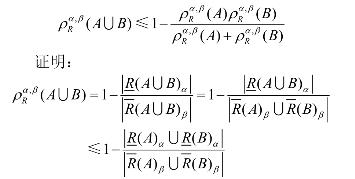
假设

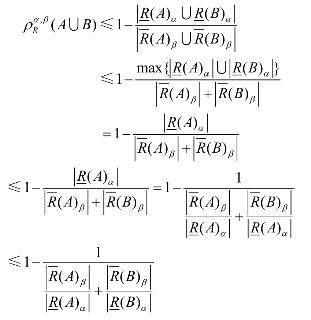
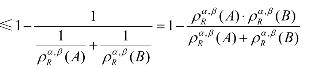
类似的，若也可证得相同结论。

定理5设U是非空有限论域，R是U上的模糊自反关系，,() A B F U∈　，参数,αβ满足则有

证明

定理6　设U是非空有限论域，R是U上的模糊自反关系，,() A B F U∈　，0 1 βα＜≤≤，若，则有

证明　由A−B = A∩～B有

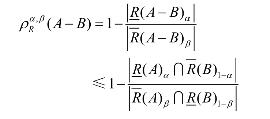
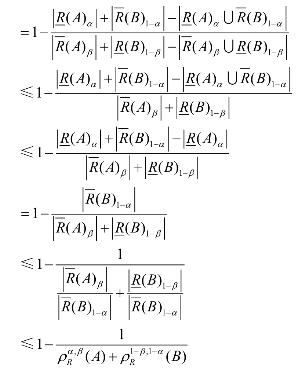
定理7设U是非空有限论域，R是U上的模糊自反关系，,() A B F U∈　，参数,αβ满足0＜β≤α≤1，则有

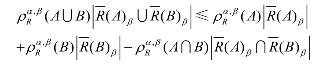
参考文献

[1] A. Zadeh. FuzzySets. Information and Control, 1965

[2] M. Banerjee, S. K. Pal. Roughness of fuzzy set[J]. Information Scienees. 1996, 93: 235-246

[3] 张文修，吴伟志等. 粗糙集理论与方法[M]. 北京：科学出版社，2001

[4] 陈水利，李敬功，王向公. 模糊集理论及其应用[M]. 北京：科学出版社，2013

[5] S. Bodjanova. APProximation of fuzzy concepts in decision making[J]. Fuzzy Sets and Systems. 1997, 85: 23-29

[6] D. Dubois, H. Prade. Two fold fuzzy sets and rough sets-some issues in bowledge representation[J]. Fuzzy Sets And Systems, 1987, 23: 3-18