对称鱼嘴构造流变计

对称鱼嘴构造流变计_香肠构造与流变学

第九节　对称鱼嘴构造流变计

利用小构造来恢复岩石的古流变性质值得探索（Czeck等，2009），本节尝试利用对称鱼嘴构造来定量研究相邻能干层黏度的相对值。

一、原理

为研究的方便，这里引入Wegmann（1932）的鱼嘴构造的演化模型，将其演化过程中的五个不同的状态近似地看成A、B、C、D、E五种不同的鱼嘴状态（图3-7）。利用鱼嘴状构造恢复岩层初始厚度已有较为系统的阐述和总结（详见第三章第二节），以B型和C型鱼嘴构造为研究对象（图3-6、图3-7），本节直接利用前人公式和结论来进一步探讨。

由于鱼嘴状构造可视为平面应变产物，适用于真应变差折射流变计（曾佐勋等，1999）（详见第四章第十二节），利用式（4-62）即可以求得能干层与基质的黏度比。

故下面我们以公式（4-62）为基础来做进一步推导：

ηＬ₁/ηL₂＝［（ηL₁/η_M）/（ηL₂/η_M）］

　　　　　＝［（ε₁－ε₃）M/（ε₁－ε₃）L₁］/［（ε_１－ε₃）M/（ε₁－ε₃）L₂］

　　　　　＝（ε₁－ε₃）L₂/（ε₁－ε₃）L₁

式中：ηL1、ηL2分别表示黏度为ηM的公共基质层两侧能干层的黏度。

第一步：通过恢复原层厚度，求出Z轴方向上的线应变ε₃：

式中：ΔH是H0与H1之差；H0为能干层的初始厚度。

第二步：通过等面积法，在第一步的基础上求出X方向上的线应变ε₁。设定对称鱼嘴状香肠构造变形前后XZ剖面上的面积相等，则有：

式中：L₀为香肠体的原长；l′为香肠体变形后的长度；D为香肠体XZ剖面面积。可看出实测l′的长度的大小并不影响ε₁的值，因此，该公式在一定程度上可以弥补由于香肠构造伸展方向上标本不完整而带来的误差。

第三步：求取能干层L₁对能干层L₂的黏度比，联立式（4-54）～（4-56）可得：

ηL1／ηL2＝（ε₁－ε₃）_L2／（ε₁－ε₃）_L1

　　　　　　＝［（H0／H1－1）－（H1／H0－1）］_L2／［（H0／H1－1）－（H1／H0－1）］_L1

　　　　　　＝（H0／H1－H1／H0）_L2／（H0／H1－H1／H0）_L1

因此，只要测算得两相邻能干层中对称鱼嘴构造的初始厚度H0和变形后厚度H1，就可以利用式（4-57）估算相邻能干层岩石的黏度比大小，此即对称鱼嘴构造流变计。

二、验证

要验证本节提出的对称鱼嘴构造流变计，只需验证式（4-57）的正确性。Treagus和Lan（2004）利用有限元模拟法给出很多黏度比的香肠构造模拟结果，下面我们以他们能干层相对基质的黏度比（m）分别为10和5的模拟成果为依据，来验证公式（4-57）。

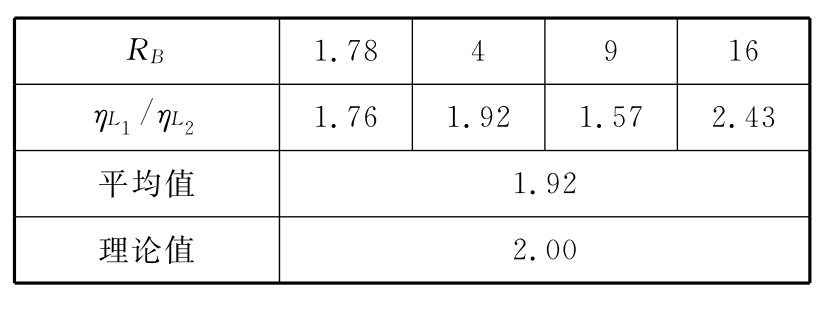
测量图4-31中变形后的模型厚度（H₁/2），测得数据见表4-17。由于基质黏度相同，则两相邻鱼嘴构造香肠体的黏度比为2，把表4-17中的测得数据代入公式（4-57），可得到如下数据（表4-18）。

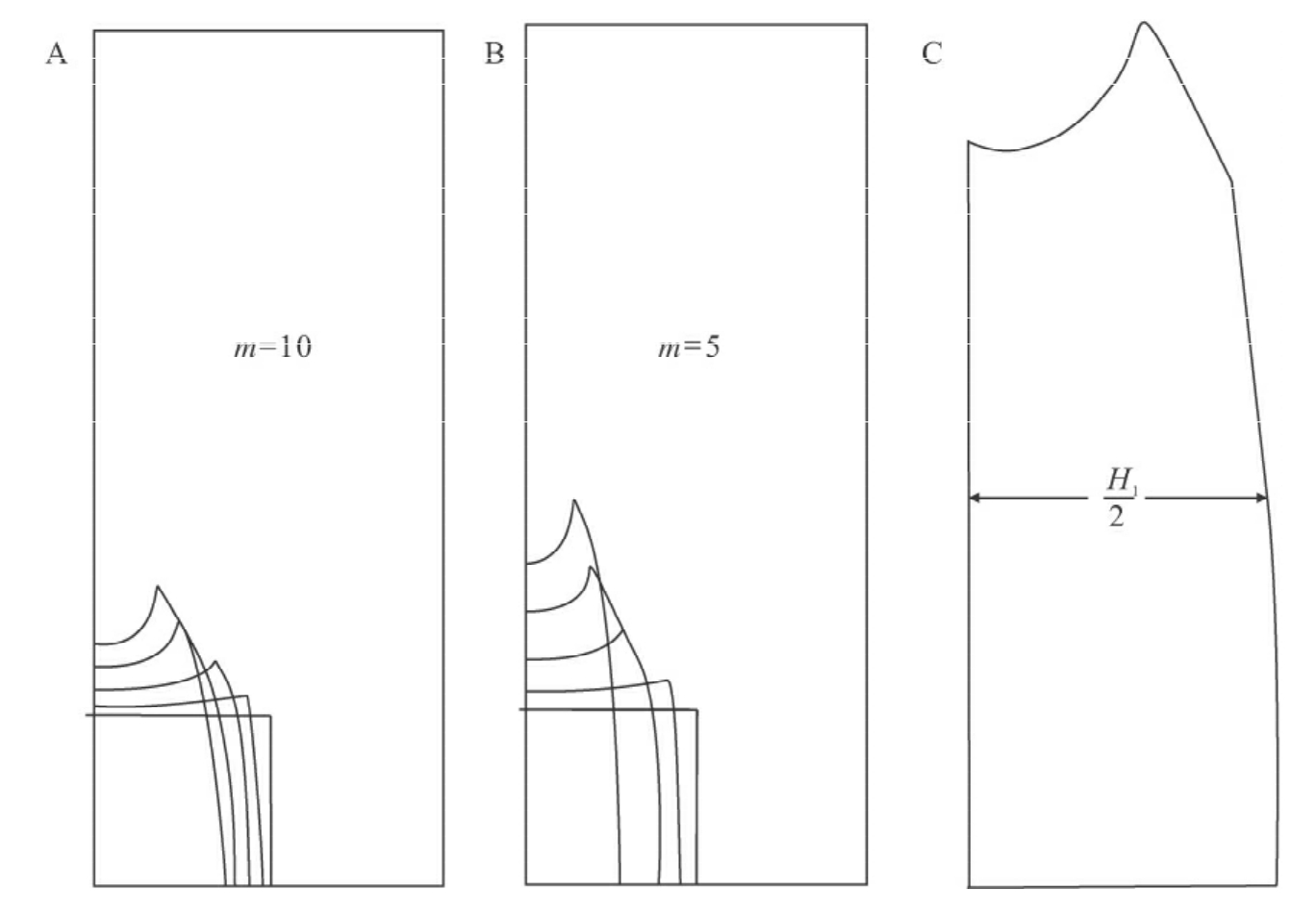
图4-31　方形物体在剪应力作用RB＝1（原始形状）、1.78（缩短25%）、4（缩短50%）、9（缩短67%）、16（缩短75%）下在基质中发生连续鱼嘴化变形（模拟的是对称鱼嘴构造“鱼嘴”一半部位的变形）

图A和B表示黏度比m分别为10和5的能干层发生的形变模拟图（据Treagus和Lan，2004）；图C表示对变形的矩形物体形态参数的定义（据Treagus和Lan，2000）

比较测算的平均值和理论值（表4-18），两者偏差在允许误差范围内，说明公式（4-57）在一定的误差范围内适用。

表4-17　实验测量数据列表

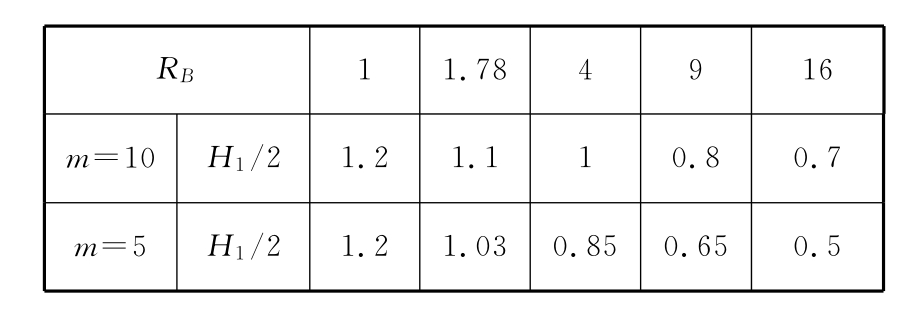
表4-18　计算结果列表

三、实例应用尝试

研究的对称鱼嘴构造标本（图4-32）采自湖北大冶铁山，香肠体岩性为角岩，基质层为大理岩。

图4-32　铁山大理岩基质中角岩对称鱼嘴状香肠构造样品图（林彦蒿和曾佐勋，2010）

H₁.石香肠的厚度；S.鱼嘴长度；S＞H₁（实例1）

1.应用实例一（图4-32A）

通过与Wegmann（1932）的模式对比，图4-32A中的第一层和第二层对称鱼嘴状石香肠分别属于B、C两种类型。于是可以直接利用式（3-4）及表3-5给出的鱼嘴构造能干层厚度恢复系数K计算，其步骤如下。

第一步：通过恢复原岩厚度，求出Z轴方向上的线应变ε₃

通过对标本的测量和计算，得到以下数据：

　　第一层（B型）：HH₁＝0.40cm；S＝0.38cm；

　　代入式（3-4），得到：HH₀＝0.402　5cm

　　第二层（C型）：HH₁＝0.88cm；S＝0.65cm；

　　代入式（3-4），得到：H₀＝0.897cm

第二步：把第一步得出的数据代入式（4-57）中，可得：

ηL₁/ηL₂＝（H₀/H₁-H₁/H₀）_L2/（H₀/H₁-H₁/H₀）_L1

　　　　 ＝（0.897/0.88-0.88/0.897）_L2/（0.402　5/0.4-0.4/0.402　5）_L1

　　　　 ＝3.07

此处的ηL₁/ηL₂＝3.07即是标本中第一层对称鱼嘴状石香肠角岩与第二层鱼嘴状石香肠角岩的黏度比。也就是说，第一层角岩的能干性明显大于第二层角岩的能干性。这种差异可能与原岩（灰质泥质）中泥质和灰质成分含量比例的不同有关。

2.应用实例二（图4-32B）

与Wegmann（1932）的模式对比，图4-32B中的第一层和第二层对称鱼嘴状石香肠分别属于C、B两种类型。于是直接利用式（3-4）计算，步骤如下。

第一步：通过恢复原岩厚度，求出Z轴方向上的线应变ε₃

通过对标本的测量和计算，得到以下数据：

　　第一层（C型）：H₁＝0.10cm；S＝0.81cm；

　　代入式（3-4），得到：H₀＝1.053cm

　　第二层（B型）：H₁＝0.10cm；S＝0.76cm；

　　代入式（3-4），得到：H₀＝0.798cm

第二步：把第一步得出的数据代入式（4-57）中，可得：

ηL₁/ηL₂＝（H₀/H1-H1/H0）_L2/（H₀/H₁-H₁/H₀）_L1

　　　　 ＝（0.798/0.10-0.10/0.798）_L2/（1.053/0.10-0.10/1.053）_L1

　　　　　＝0.75

此处的ηL₁/ηL₂＝0.75即是标本中第一层对称鱼嘴状石香肠角岩与第二层对称鱼嘴状石香肠角岩的黏度比。也就是说，第一层角岩的能干性明显小于第二层角岩的能干性。同样，这种差异也可能是由原岩中泥质和灰质成分含量比例的差异引起的。

四、讨论与结论

本节利用对称鱼嘴状香肠构造估算相邻能干层的黏度比，并引用Treagus和Lan（2004）部分有限元模拟成果，验证了公式（4-57）的正确性，也再次应用鱼嘴状石香肠构造推算岩层初始厚度的方法。该对称鱼嘴构造流变计的优点在于，在实践时只需要测量鱼嘴状岩层的厚度H1和鱼嘴长度S，并准确判断出鱼嘴构造的类型，代入公式（3-4）和（4-57）便能简便地计算出鱼嘴构造相邻能干层的黏度比，可避免野外标本的不完整给我们带来的计算误差。

在该流变计公式推导过程中，式（4-56）将香肠体变形前后的ac面均视为矩形，结合鱼嘴构造的演化特征（图3-7），我们认为该流变计应用于B、C型鱼嘴构造时产生的偏差较小；而对D、E型鱼嘴构造，由于其ac面较大程度地偏离了矩形，可能测得结果的偏差会变大。另外，该方法还需要通过获取更多的实例研究来验证其测算结果的可靠性，并探讨出更为具体的适用范围。