均值分类算法的基础

4．2．1　k均值分类

k均值算法能使聚类域中所有样本到聚类中心的距离平方和最小。其主要步骤如下:

第一步:任选k个初始聚类中心: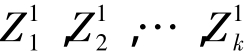(上角标记载为寻找聚类中的迭代运算次数)。用数组classp［6*clsnumber］来存储类中心的值，一般可选定样品集的前k个样品作为初始聚类中心。但是考虑到这样做不太有利于后面的算法收敛。因此采用了最大最小距离选心法。该法的原则是使各初始类别之间，尽可能地保持远离。

任意选取50个初始中心，将其值存入iGrayValue［6*50］中，将第一个点X₁作为第一个初始类别的中心Z₁。

计算X₁与其他各抽样点的距离D。取与之距离最远的那个抽样点(例如X₇)为第二个初始类别中心Z₂，则第二个初始类中心Z₂=X₇。

对剩余的每个抽样点，计算它到已有各初始类别中心的距离D_ij(i，j=1，2，…，已知有初始类别数m)，并取其中的最小距离作为该点的代表距离D_j:

D_j=min(D_1j，D_2j，…，D_mj)

在此基础上，再对所有各剩余点的最小距离D_j进行相互比较，取其中最大者，并选择与该最大的最小距离相应的抽样点(如X₁₁)作为新的初始类中心点，即Z₃=X₁₁，此时m=m+1。

如此迭代直到m≥clsnumber，即m=0，1，2，…，clsnumber。

第三步:计算各聚类中心的新向量值classo［i］;

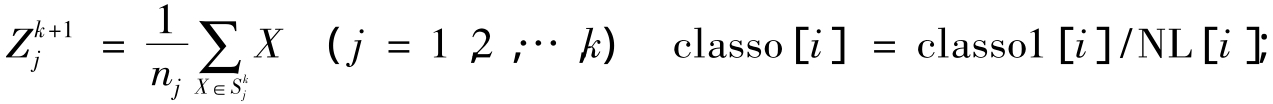
式中:n_j为S_j中所包含的样品数;classo1［i］表示所有属于第i类的像素的值的累加;NL［i］表示属于第i类的像素总数;classo［i］为重新分类后的聚类中心值。

因为在这一步要计算k个聚类中心的样品均值，故称为k均值算法。

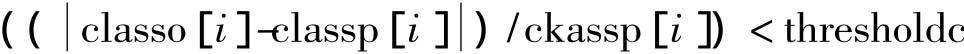
就可以结束算法。

k均值算法的特点是:k均值算法的结果受到所选聚类中心的个数k及初始聚类中心选择的影响，也受到样品的几何性质及排列次序的影响。实际上，需试探不同的k值和选择不同的初始聚类中心。如果样品的几何特性表明它们能形成几个相距较远的小块孤立区，则算法多能收敛。图4-2给出聚类类别数为5、最大改变阈值为5、最大迭代次数为5时的k均值分类效果图。

图4-2　k均值分类算法效果图