物方空间几何约束的房屋模型三维重建

7．1．3　物方空间几何约束的房屋模型三维重建

基于平差模型和简单房屋物方的多种约束条件，简单型房屋半自动重建的基本框架如图7-7所示。

若采用图7-7所示的系统框架进行简单房屋的半自动重建，有如下特点:

(1)房屋在重建前由操作员选择房屋类型，并通过人机交互界面输入少数的种子点，在选择种子点时优先考虑主框架(屋脊)上的点，主要出发点是:

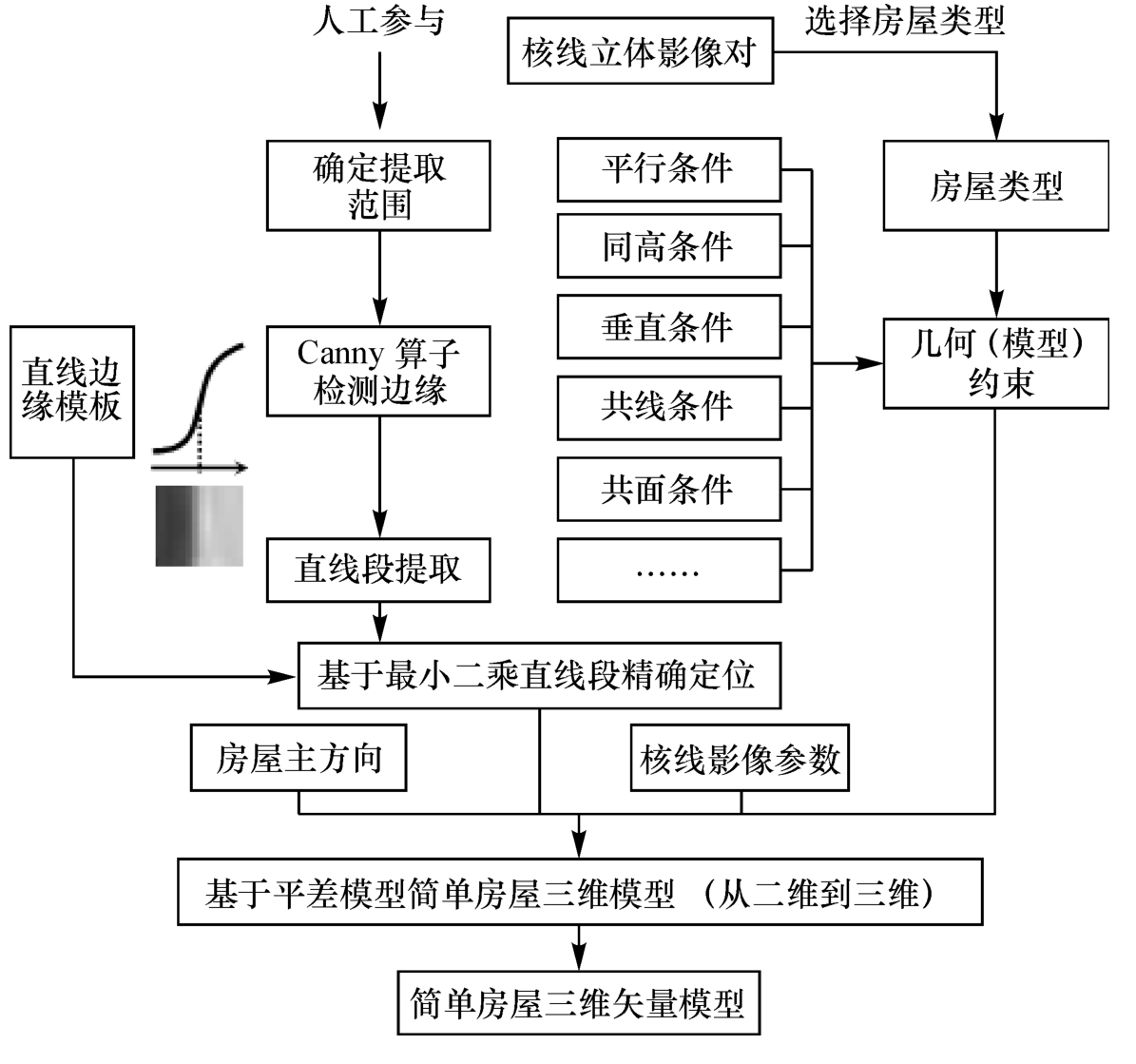
图7-7　简单型房屋半自动重建的基本框架

①屋脊决定了房屋的基本走向。

②选定屋脊后，其他的约束条件一般都与屋脊平行或垂直。

③屋脊上的点最清晰，一般不会有遮挡。

(2)首先根据不同结构将房屋分类，便于灵活地组合各种几何约束条件，构建不同的平差模型。

(3)在选择好房屋类型并给定少数种子点后，其余的重建工作由算法自动完成。主要优点在于:

①一般只需要两个种子点即可完成房屋结构信息的获取，量测工作量大大减少。

②主框架结合直线模板匹配，提供了较好的初始值，使得平差解算更加稳定。

③基于最小二乘模板匹配技术进行房屋边缘的精确定位，重建精度可靠。

(4)在立体像对下进行，采用核线约束条件确定房屋特征点的三维信息，可直接得到房屋的三维模型。在立体像对下充分利用房屋的物方空间几何约束来提高由于噪声和特征不足时算法重建的稳定性。

在提取的很多线段中，房屋的主方向隐含着一种基本的拓扑关系和度量关系，因此，本章力图解决基于主方向的简单房屋的半自动重建问题。

图7-8以人字形房屋为例表示了简单型房屋三维重建的一般流程。以人工给出房屋屋脊两端点的近似值并且事先选定房屋类型作为已知条件。如果只给一个点将很难确定房屋的大小，也无法克服噪声干扰，如果给出主方向(屋脊)两端点，则其他点均与主方向平行或垂直，以下简要介绍重建的步骤。

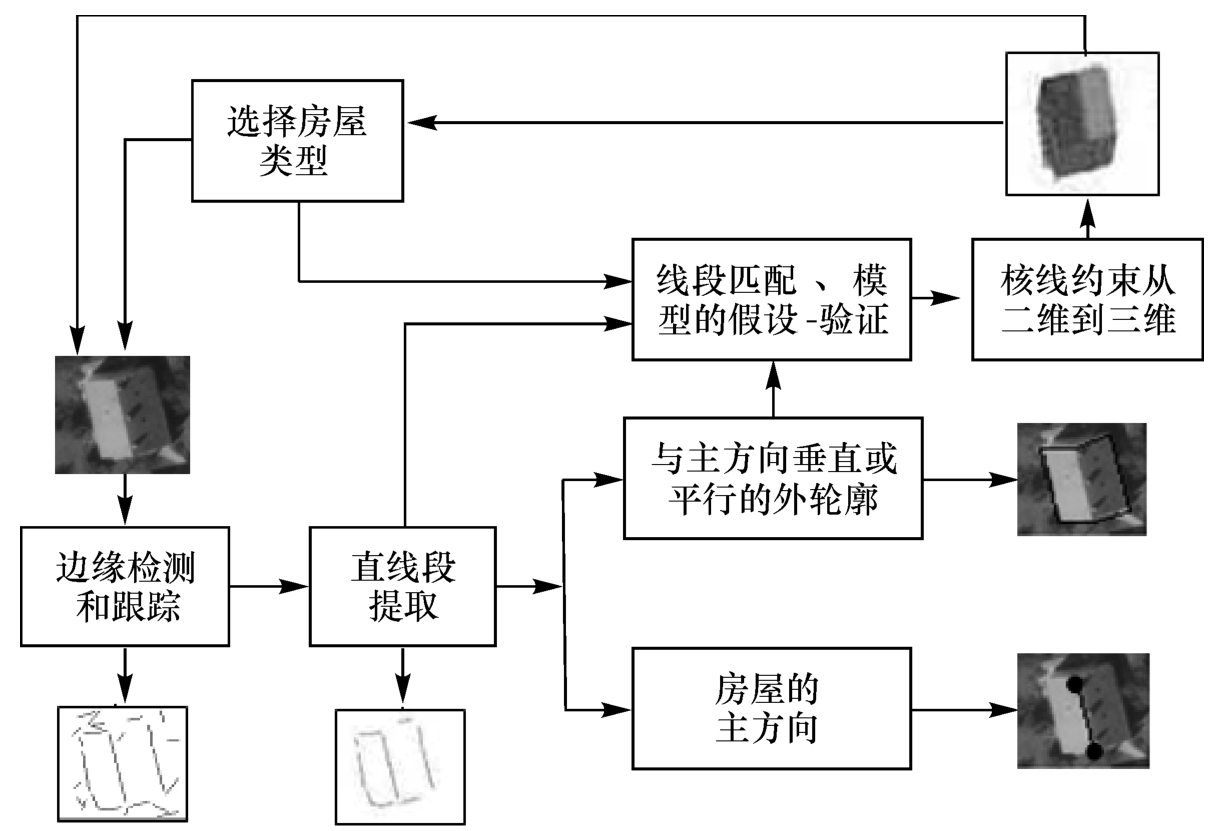
图7-8　人字形房屋三维重建流程

(1)边缘检测与跟踪。在搜索范围内以Canny算子作为边缘检测算子检测出房屋边缘信息。

(2)直线段提取，从边缘矢量得到直线段。

(3)根据房屋的主方向，结合房屋的内拓扑和度量约束条件，从而确定外轮廓。

(4)线段的测试—验证过程。输入的房屋的类型给出了一个明确的几何结构和约束，包括房屋角点和各边之间的几何关系。其测试—验证过程就是要从提取的直线段中组合出给定的房屋结构来。逐一将提取的直线段的几何属性与已知的加了标号的屋顶结构进行比较测试，差距小于阈值的被证实，而其他的线段则被剔除。在已知屋顶结构的情况下，只需要确定少数线段就能恢复出整个屋顶的结构。

(5)上述的提取是在二维影像上进行的，为了得到房屋角点的三维坐标，还要通过核线约束条件，并进行前方交会，最终得到各个角点的物方三维坐标，实现房屋的三维模型重建(见图7-9)。

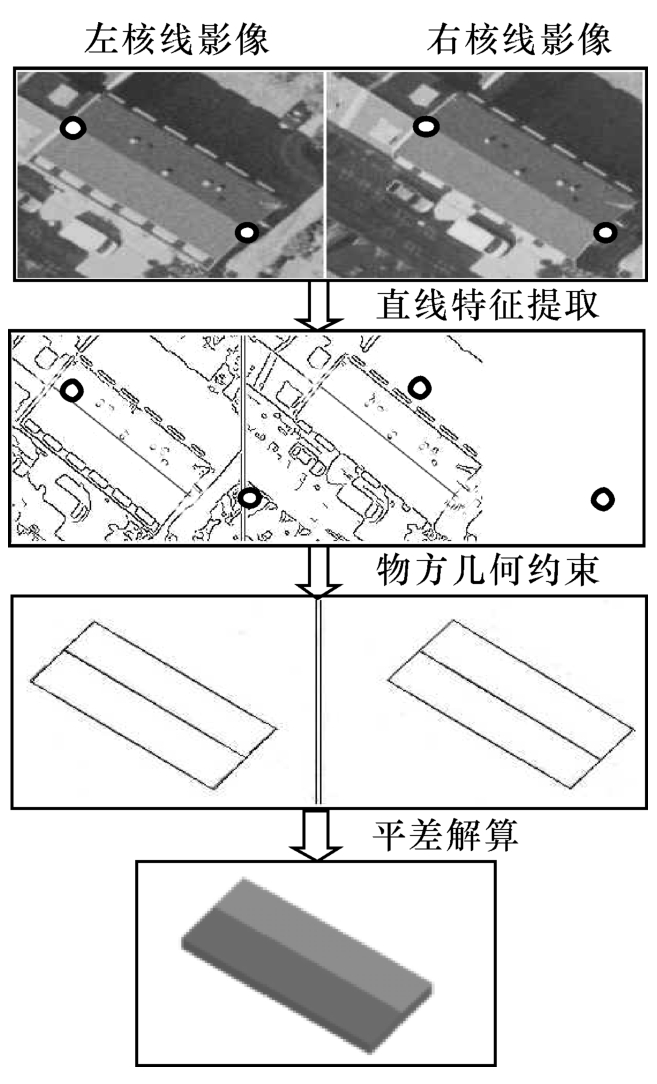
图7-9　人字形简单型房屋的三维重建过程

人字形简单型房屋是房屋中类型最多的一种，图7-10为另一个核线影像对上的人字形房屋的原始影像，图7-11为得到的房屋的平面模型和三维模型图。

图7-10　人字形简单房屋的原始核线影像对

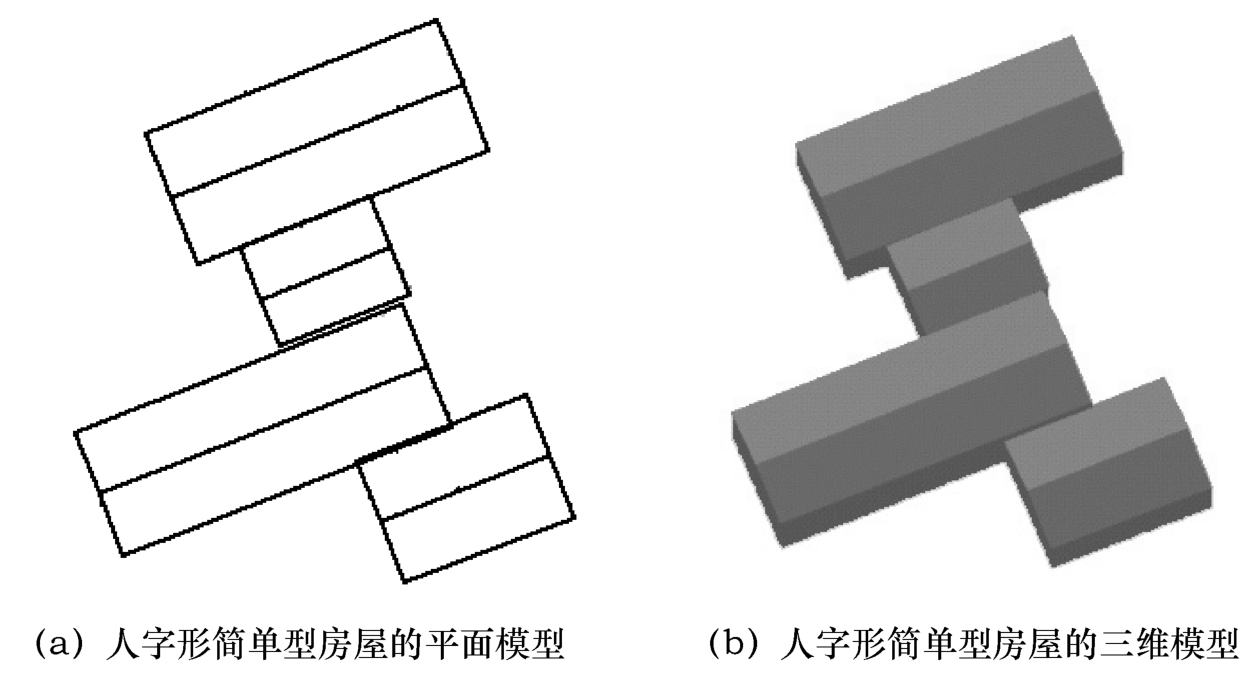
图7-11　人字形简单型房屋的三维模型

矩形简单型房屋的重建流程类似于人字形房屋，理论上主方向可选取任意一条边，实验中效果最好的是选取目标最清晰的一条边，边缘检测与跟踪后，直线段都有着彼此垂直或平行的几何约束条件，对图7-12所示的矩形结构的简单房屋，三维模型重建过程如图7-13到图7-15所示。

图7-12　矩形简单型房屋原始影像图

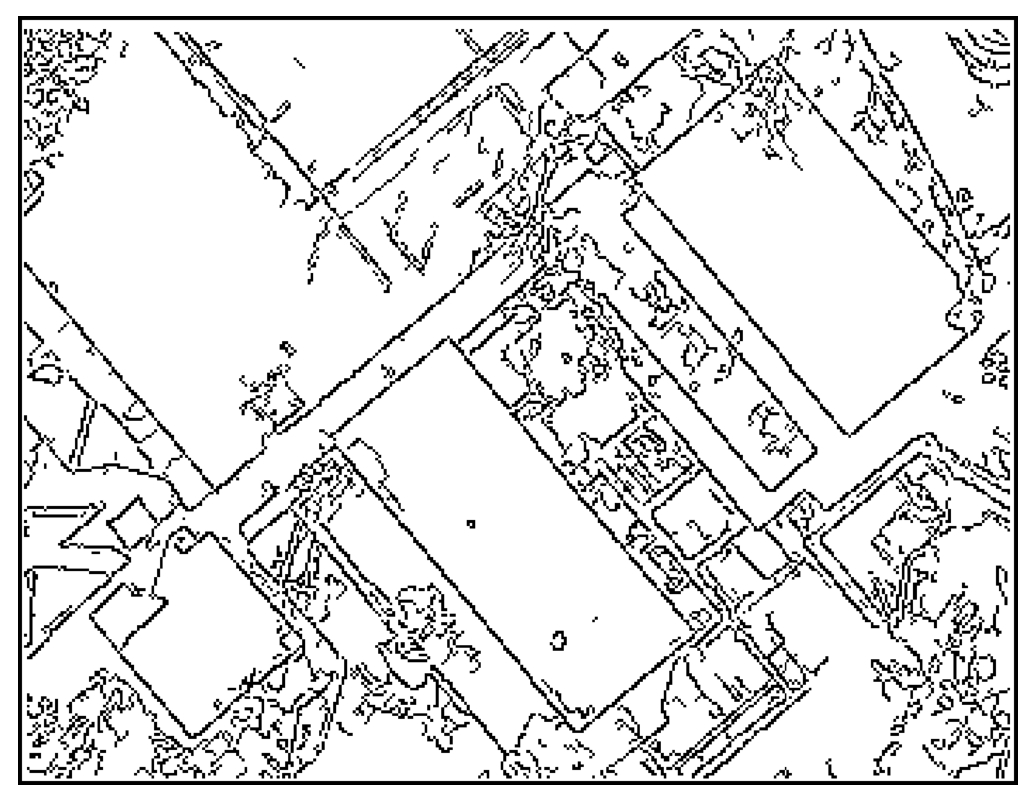
图7-13　边缘检测细化后效果图

图7-14　边缘跟踪和模板匹配后效果图

图7-15　矩形简单型房屋三维模型

由于从影像上自动提取出的屋脊线段大部分是不完全的，沿着屋脊方向重新匹配出的效果很好，而且基于主方向提取策略，使得所有其他房屋边缘都与主方向平行或者垂直，直接利用这种度量关系筛选了很多噪声，从本来无序的线条图中识别出屋顶的结构，自动重建方法准确、稳健。