序列相关性的检验

第二节　序列相关性的检验

序列相关性一般出现在以时间序列(time series)数据为样本的模型中，因此，当遇到以时间序列作为分析对象的模型时，就需要检验模型是否出现序列相关性。序列相关性检验核心便是检验随机干扰项之间是否存在相关性，因此，首先用普通最小二乘法估计模型，得到模型残差e，用残差近似代替模型随机误差项，分析残差间是否存在相关性。序列相关性的检验主要分为图示法和解析法两大类:图示法包括残差自相关图与残差时序图;解析法主要包括回归检验法、D．W．检验法、拉格朗日乘数检验法等。

下面将以实例说明如何运用各种检验方法对模型的序列相关性进行检验。

例4-1经济理论指出，商品进口主要由进口国的经济水平、商品进口价格指数和国内价格指数的对比因素决定。本例主要分析中国商品进口M与国内生产总值GDP的关系，选取了1978—2001年的国内生产总值GDP及商品进口量M，以M为被解释变量，GDP作为解释变量进行分析。表4-1为1978—2001年中国商品进口与国内生产总值。

表4-1　中国商品进口与国内生产总值

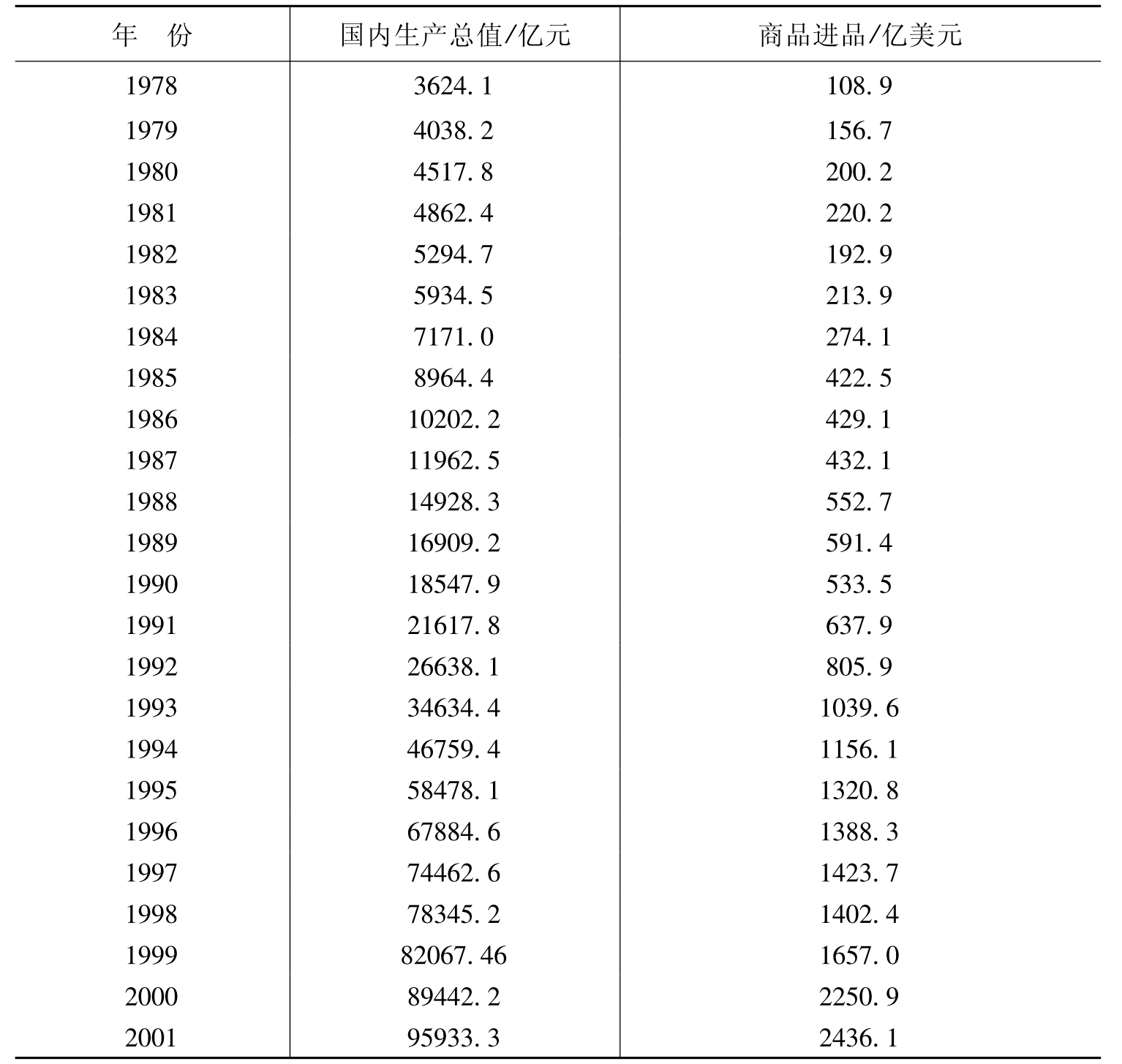
(数据来源:中国国家统计局．《2002中国统计年鉴》．北京:中国统计出版社，2002．)

1．估计模型获得残差e

在检验模型是否存在序列相关性时，首先需要获得模型的随机干扰项，但由于模型随机干扰项的值不易获得，一般用普通最小二乘估计后的残差近似替代随机干扰项。因此，首先对模型进行普通最小二乘估计，获取残差e。

估计模型形式为:

M_t=α₀+α₁GDP_i+μ_t(4-5)

在EViews下建立一新的工作文档后，录入表4-1内的数据。在命令栏内输入OLS估计命令

ls m c gdp

得到最小二乘回归结果(见图4-1)。由估计结果得到中国商品进口商品估计方程

M^{^}t=152．91+0．02GDP_t

(3．32)(20．12)(4-6)

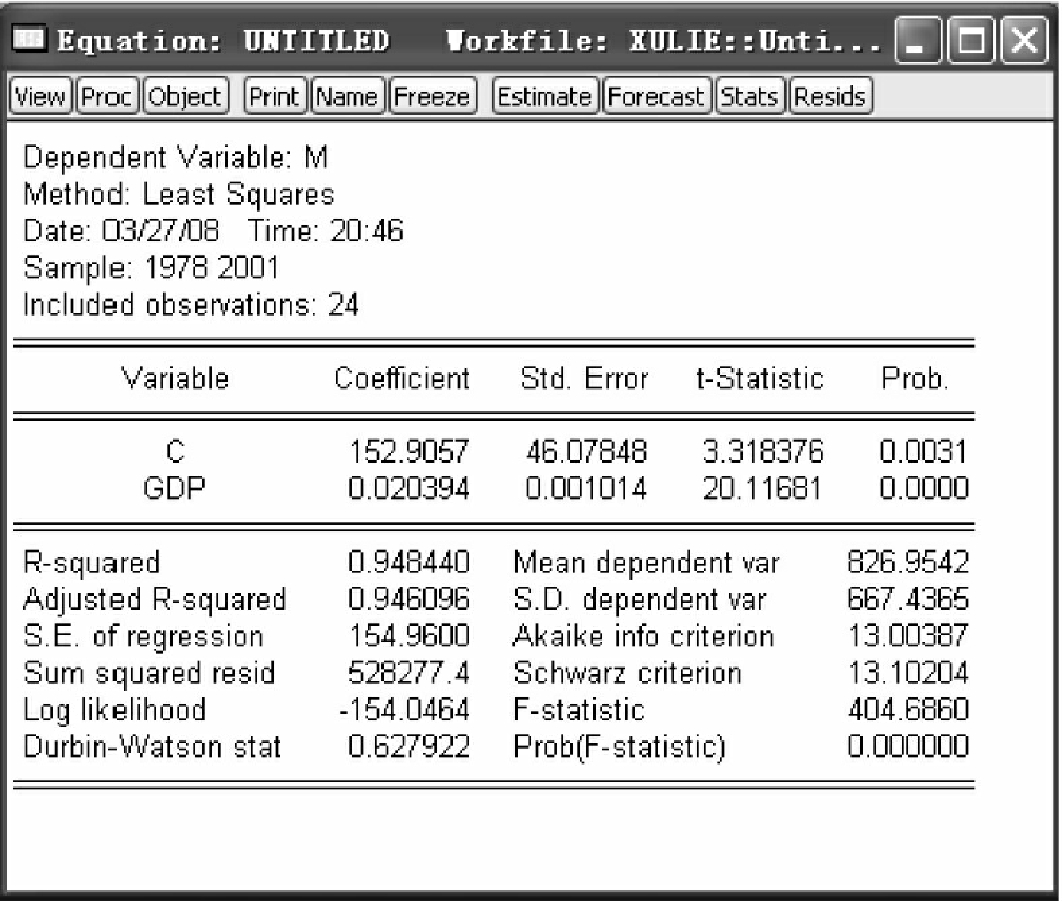
图4-1

由于每进行一次回归，残差会随之改变，因此需要保留估计残差，在命令栏内输入

genr e=resid

或在主菜单下点击Quick/Generate Series，在弹出的对话框(见图4-2)内输入

e=resid

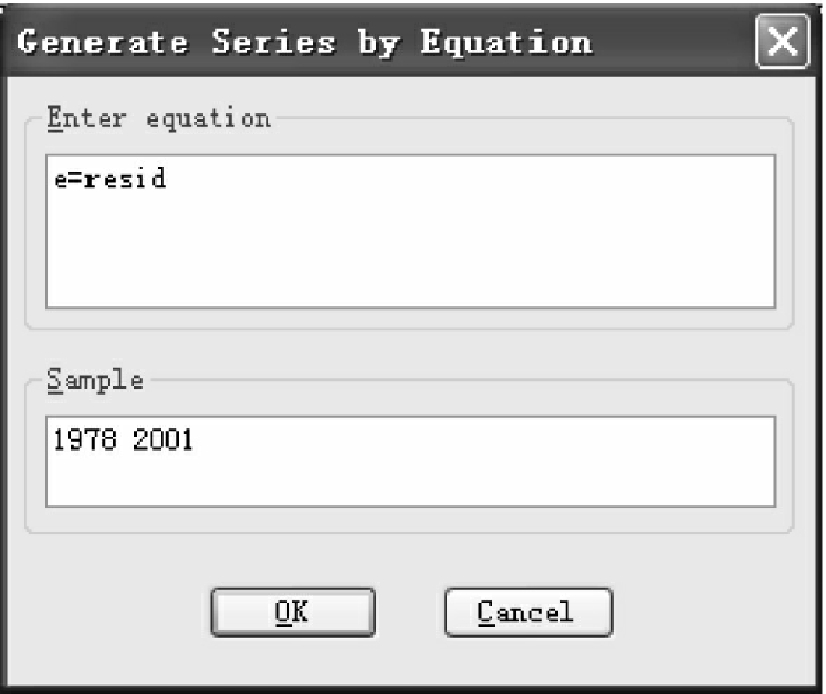
图4-2

点击OK，得到残差序列e_t，如图4-3所示。

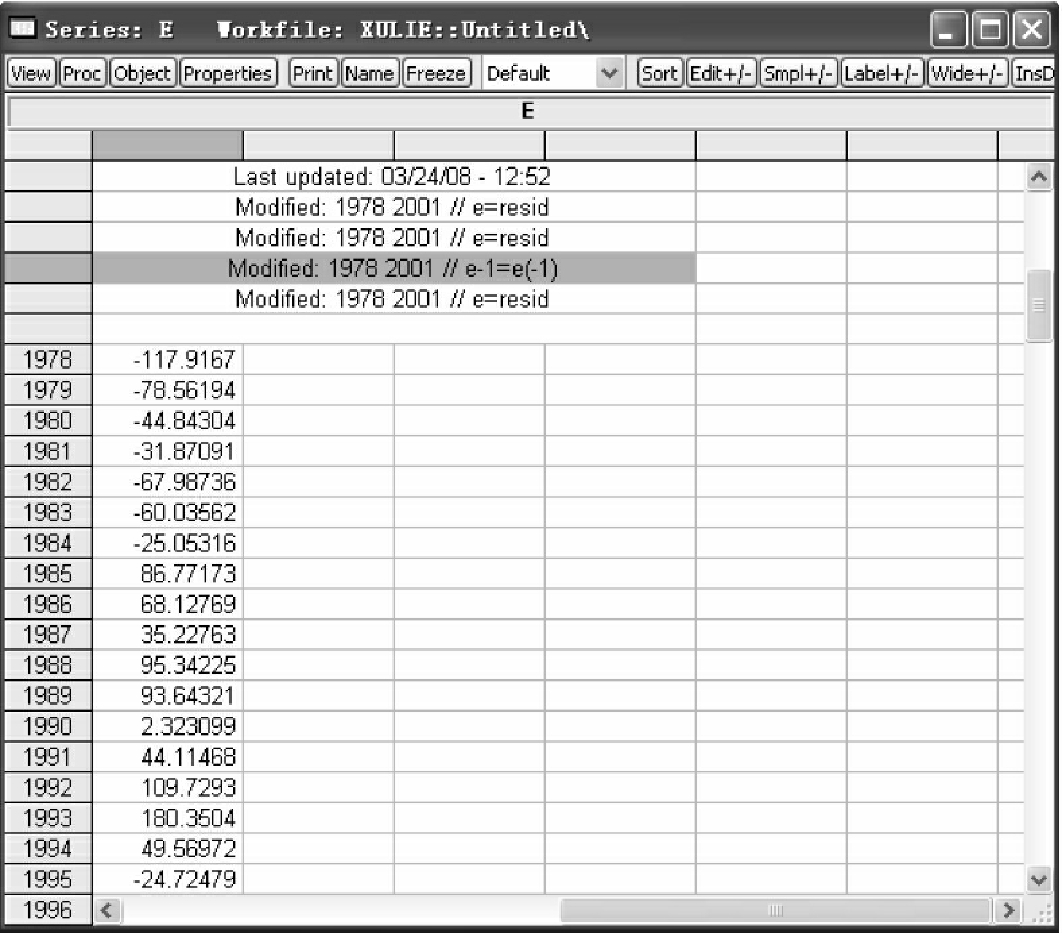
图4-3

2．图示法

由于残差e_t可以作为μ_t的估计，如果μ_t存在序列相关性，则一定会通过e_t表现出来，因此可以通过e_t的自相关图和时序图来判断随机误差项的序列相关性。

(1)残差自相关图

同样，可以通过菜单方式和命令方式做出残差自相关图。在命令栏内输入

genr e1=e(－1)

得到残差的滞后一期序列e1。将e和e1作为group打开，见图4-4，得到残差e和其滞后一期e1的spreadsheet，见图4-5。

图4-4

在图4-5中的菜单栏内点击View/Graph/Scatter/Simple Scatter(见图4-6)，得到残差自相关图。

同样，可以通过在命令栏内输入

scat e e(－1)

直接做出残差与其滞后一期的自相关图，如图4-7所示。

从图4-7中可以看出，残差和其滞后一期值基本落在第一、三象限，这表明随机误差项之间存在正相关。

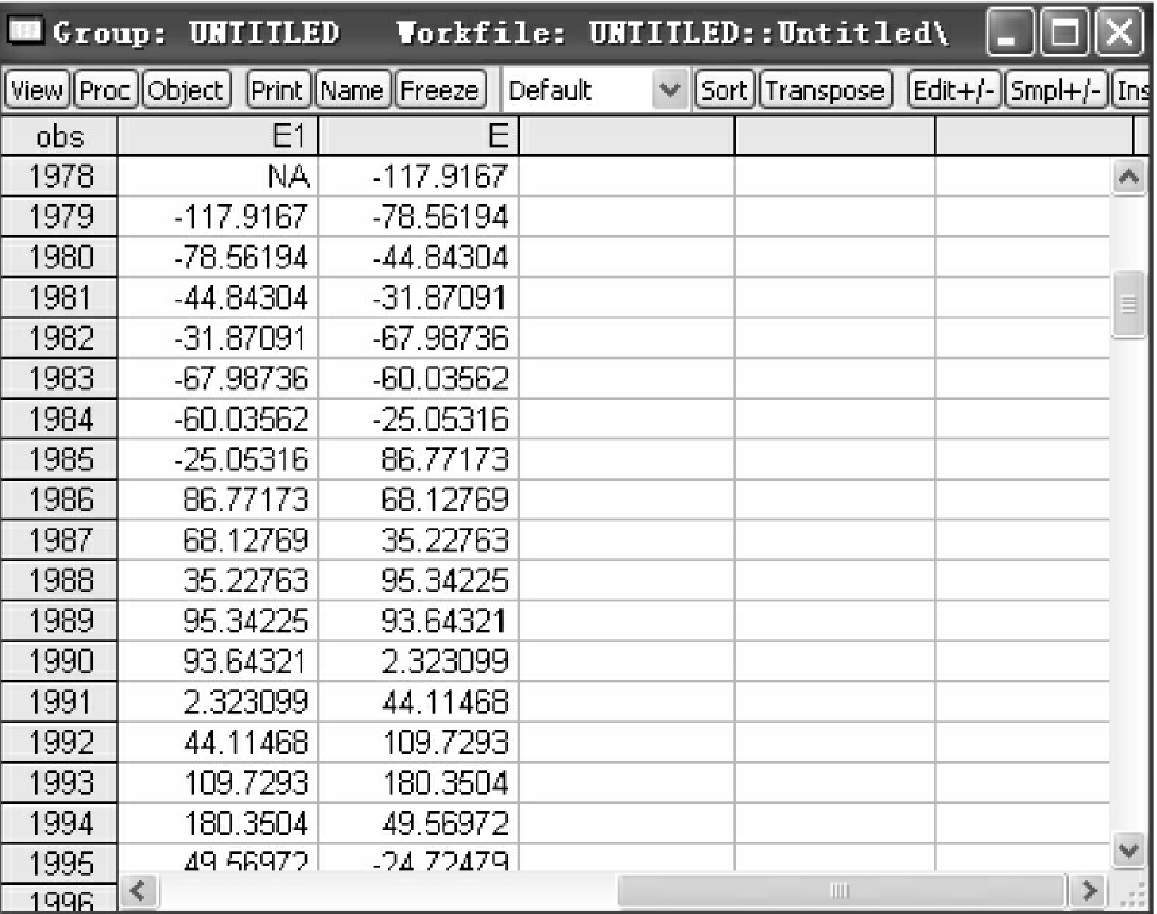
图4-5

图4-6

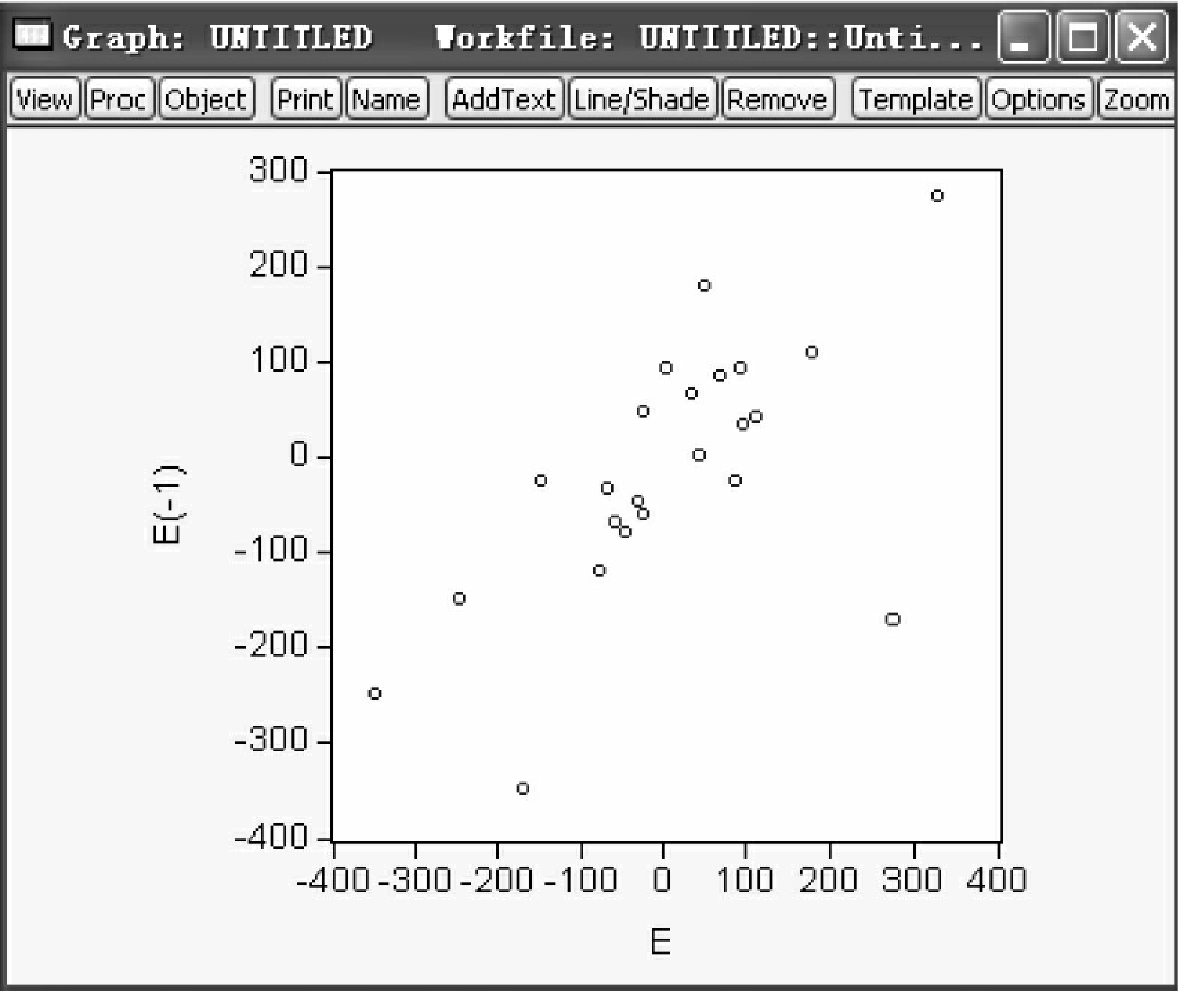
图4-7

(2)残差时序图

残差的时序图即残差随时间变化的图像。对随机项的时间序列，如果当时、随后的若干个随机项都有大于0的倾向或者当时、随后的若干个随机项都有小于0的倾向，我们说具有相关性;而负自相关则意味着两个相继的随机项具有正负相反的倾向。

在最小二乘估计结果(见图4-1)的菜单栏内点击View/Actual，Fitted，Residual/Actual，Fitted，Residual Graph，见图4-8，便可得到残差时序图(见图4-9)。

观察图4-9可发现，当时及随后的若干个随机误差项均具有大于0的趋势，从而判断，随机误差项之间呈现自相关关系。

3．解析法

(1)回归检验法

以回归残差e_t作为被解释变量，选取其滞后一期e_t－1作为解释变量，建立模型

e_t=ρe_t－1+ε_t　　　　　4-7)

图4-8

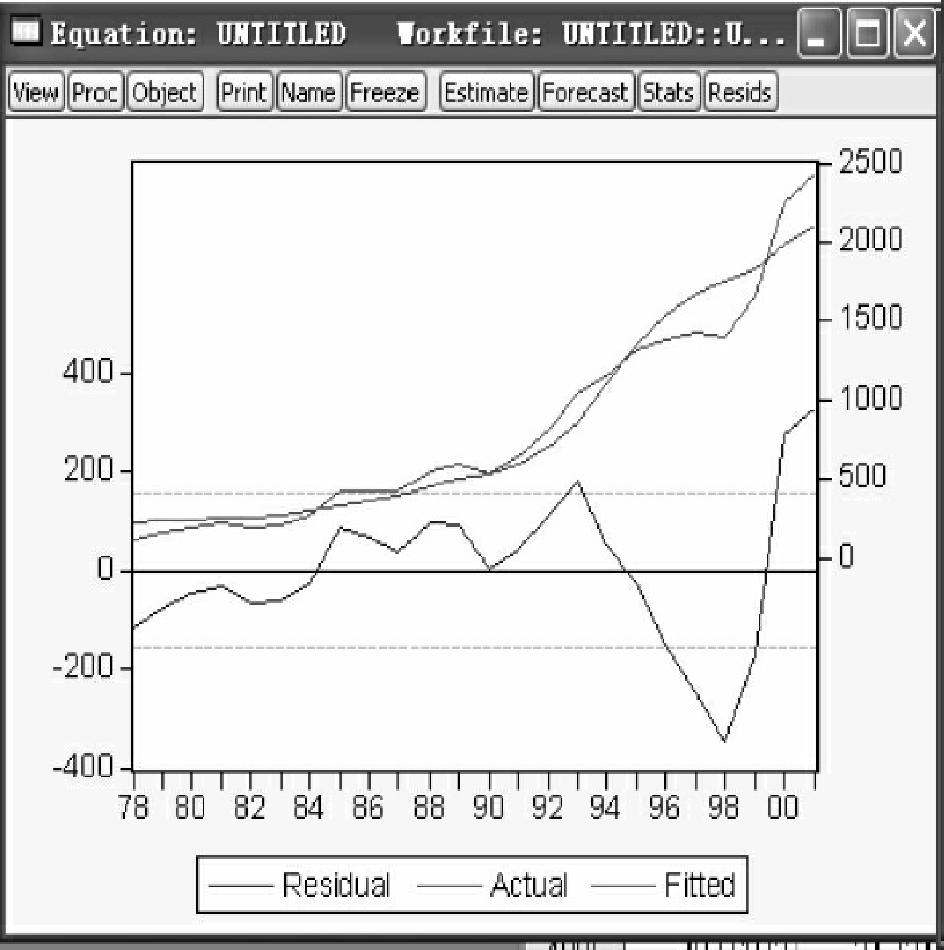
图4-9

估计模型，如果ρ不显著为0，则认为随机误差项之间存在序列相关性。对式(4-7)进行普通最小二乘估计，命令为

ls e e(－1)

得到结果如图4-10所示。

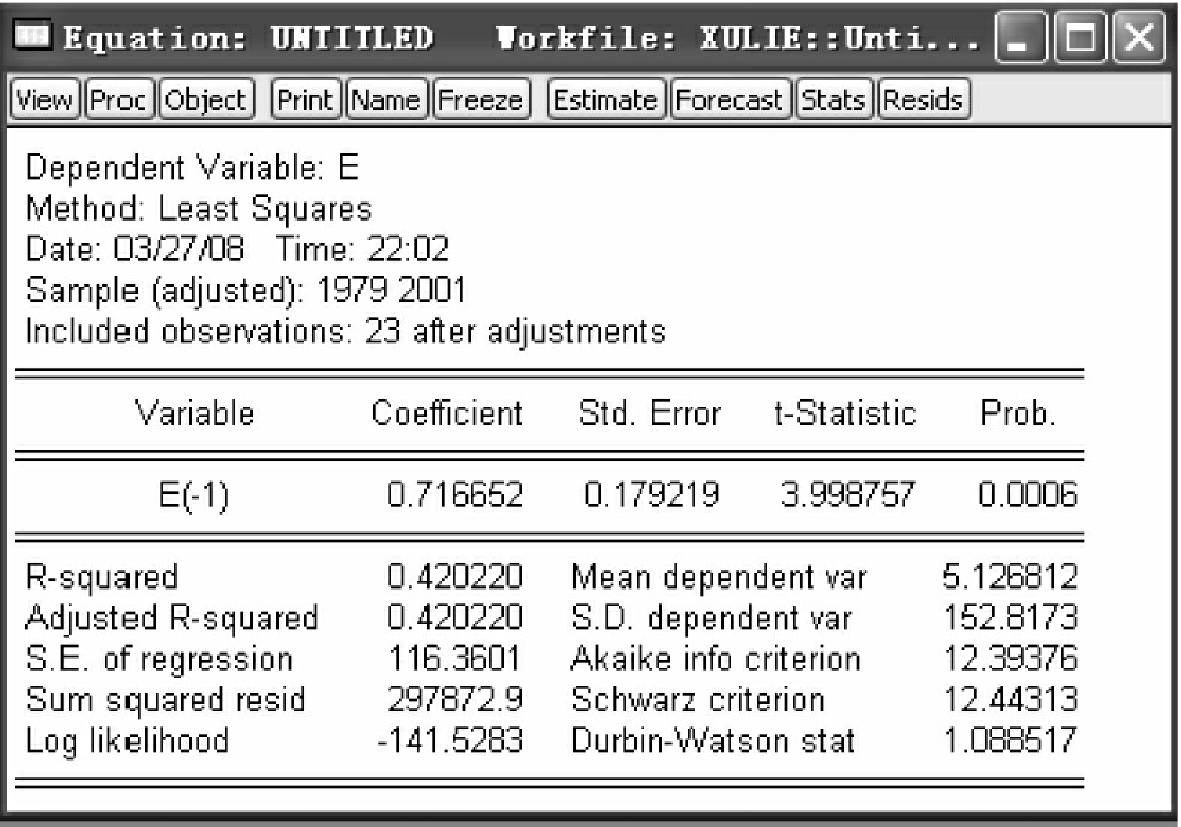
图4-10

从图4-10中可看出，解释变量前系数t统计量大于5%显著性水平(1．96)，因此，可以判断，随机误差项之间存在相关关系。当然，建立回归模型时，我们还可以将e_t－2，e²_t等作为解释变量，与e_t建立方程进行估计。只要某一种函数形式能使得方程显著成立，那么原模型就存在序列相关性。

(2)杜宾—瓦森检验法(Durbin-Watson)

在EViews下，可以直接通过D．W统计量来判断模型是否存在序列相关性。在此例中，D．W值为0．6279(见图4-1)，0＜D．W＜1．27，其中1．27为5%显著性水平下的D．W临界值，因此，可以判断模型存在序列相关性。

(3)拉格朗日乘数检验(Lagrange multiplier)

拉格朗日乘数检验发展了D．W检验，适用于高阶序列相关的检验，又称GB检验。EViews直接提供了拉格朗日检验的结果。在图4-1中，原模型回归结果下点击View/Residual Test/Serial Correlation LM Test，如图4-11所示。

随后弹出对话框，选择滞后长度，采用默认滞后长度，如图4-12所示。

图4-11

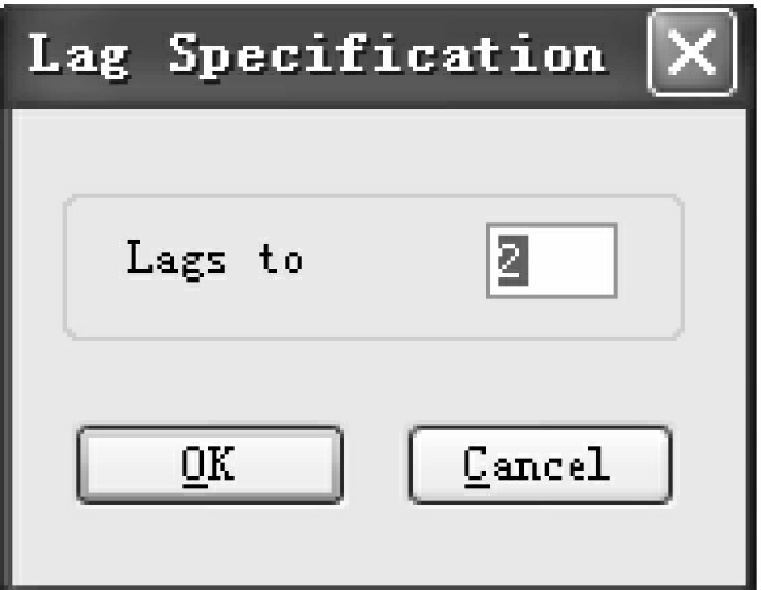
图4-12

点击OK，得到拉格朗日乘数检验结果，如图4-13所示。

分析图4-13中的结果，F=19．529，大于5%显著性水平下的临界值(3．49)。因此，拒绝模型不存在序列相关性的原假设。从图上方的概率值也可以得出相同的结论，接受原假设的概率几乎为0，即模型不存在序列相关性的概率仅为0，因此，可以判断，原模型存在序列相关性。

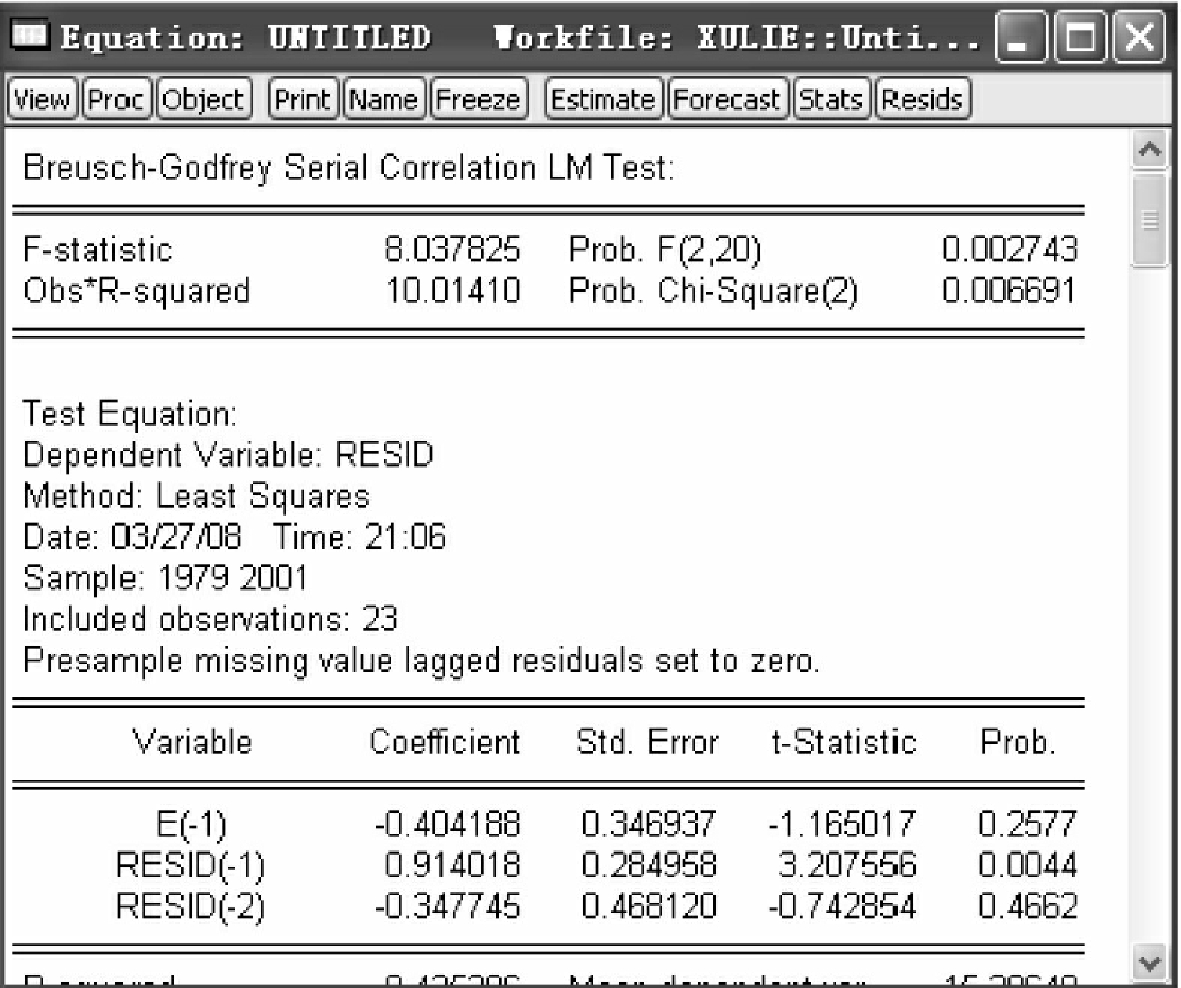
图4-13