多重共线性的实验操作

第二节　多重共线性的EViews实验操作

例5-1多重共线性的检验与操作。

选取粮食生产为例，由经济学理论和实际可以知道，影响粮食生产y的因素有:农业化肥施用量x₁、粮食播种面积x₂、成灾面积x₃、农业机械总动力x₄、农业劳动力x₅，由此建立以下方程:y=β₀+β₁x₁+β₂x₂+β₃x₃+β₄x₄+β₅x₅，表5-1　　　　　　给出了中国粮食生产的相关数据。

表5-1

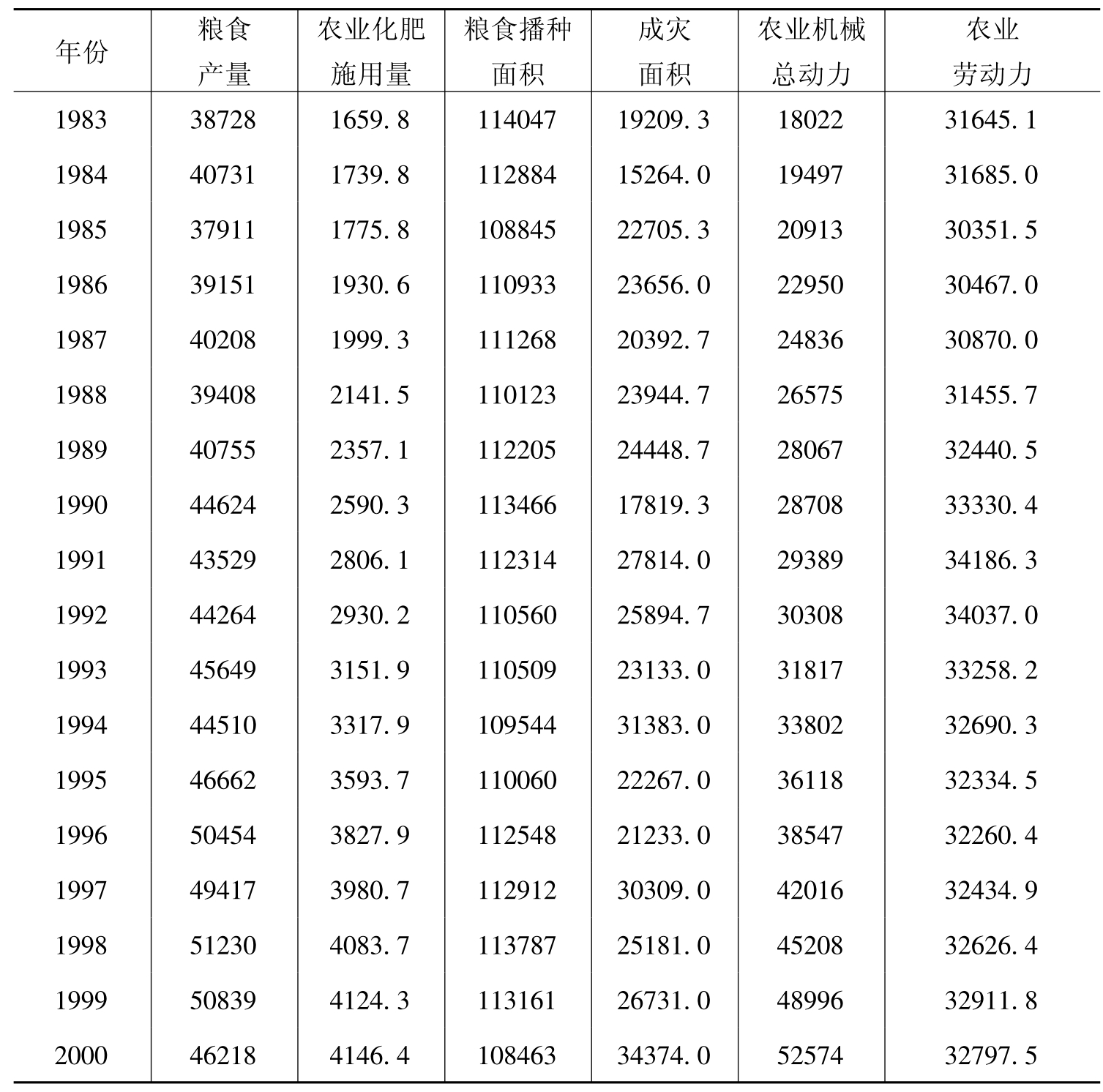
(资料来源:《中国统计年鉴》(1995—2001)

1．检验多重共线性

参照例2-1，估计模型y=β₀+β₁x₁+β₂x₂+β₃x₃+β₄x₄+β₅x₅，得到估计结果如图5-1所示。

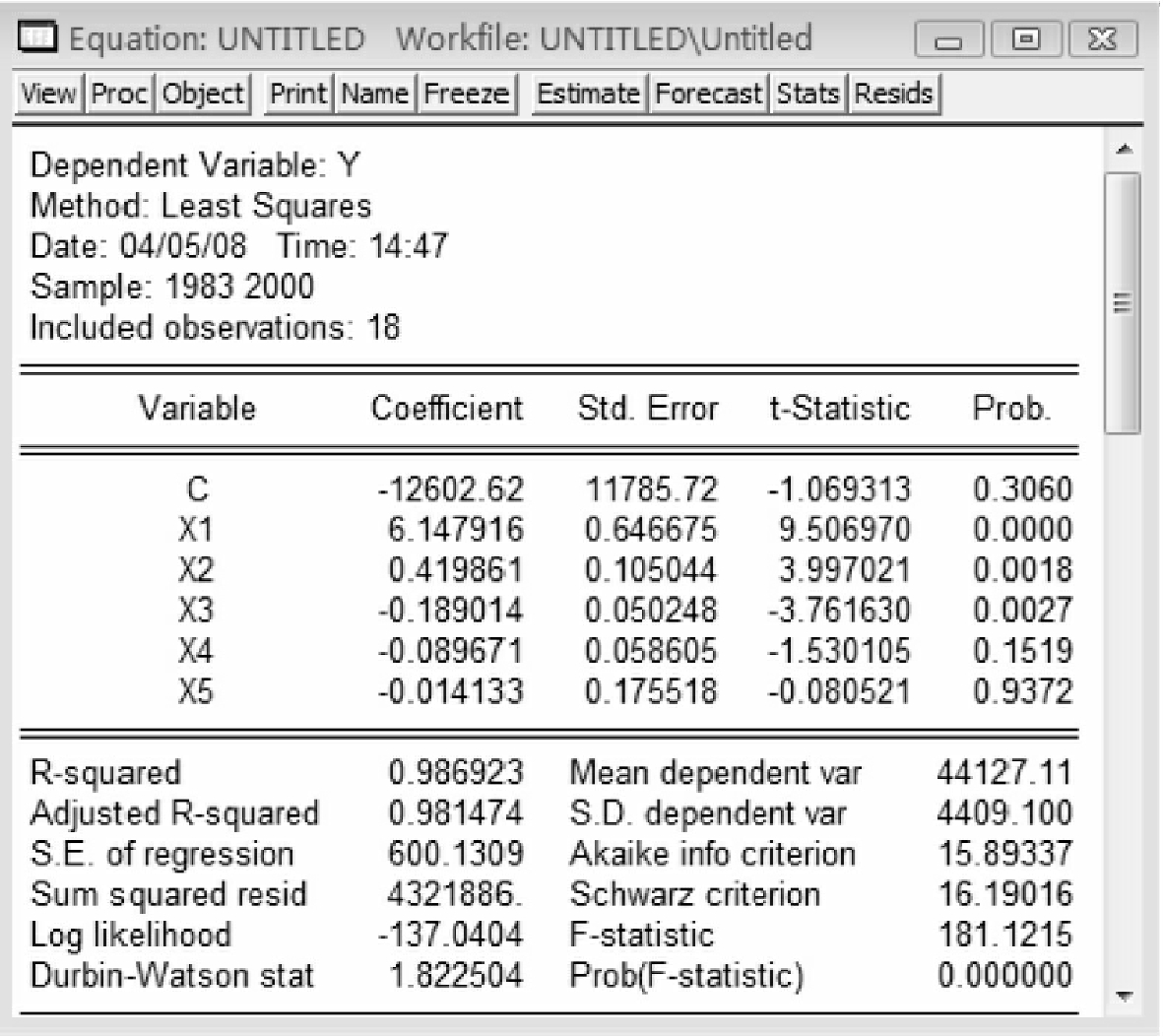
图5-1

从中可以看出R²=0．986923，F=181．1215，R²和F值均很高，说明模型的整体拟合效果很好，但是参数的t检验值有的并不显著，x4和x5的参数估计值并不显著，而且符号的经济意义也不合理，因此认为存在多重共线性。

另一方面，观察解释变量之间的相关系数。同时选中x1，x2，x3，x4，x5，点击右键open→as Group，如图5-2所示。

得到图5-3。

在该对话框中点击View→Correlations→Common Sample，如图5-4所示。

得到图5-5。

从图5-5中可以看出:x1与x4的相关系数是0．960278，存在高度相关性。因此，原模型存在多重共线性。

2．多重共线性的修正

(1)逐步回归法

第一步:首先确定一个基准的解释变量，即从x1，x2，x3，x4，x5中选择解释y的最好的一个建立基准模型。

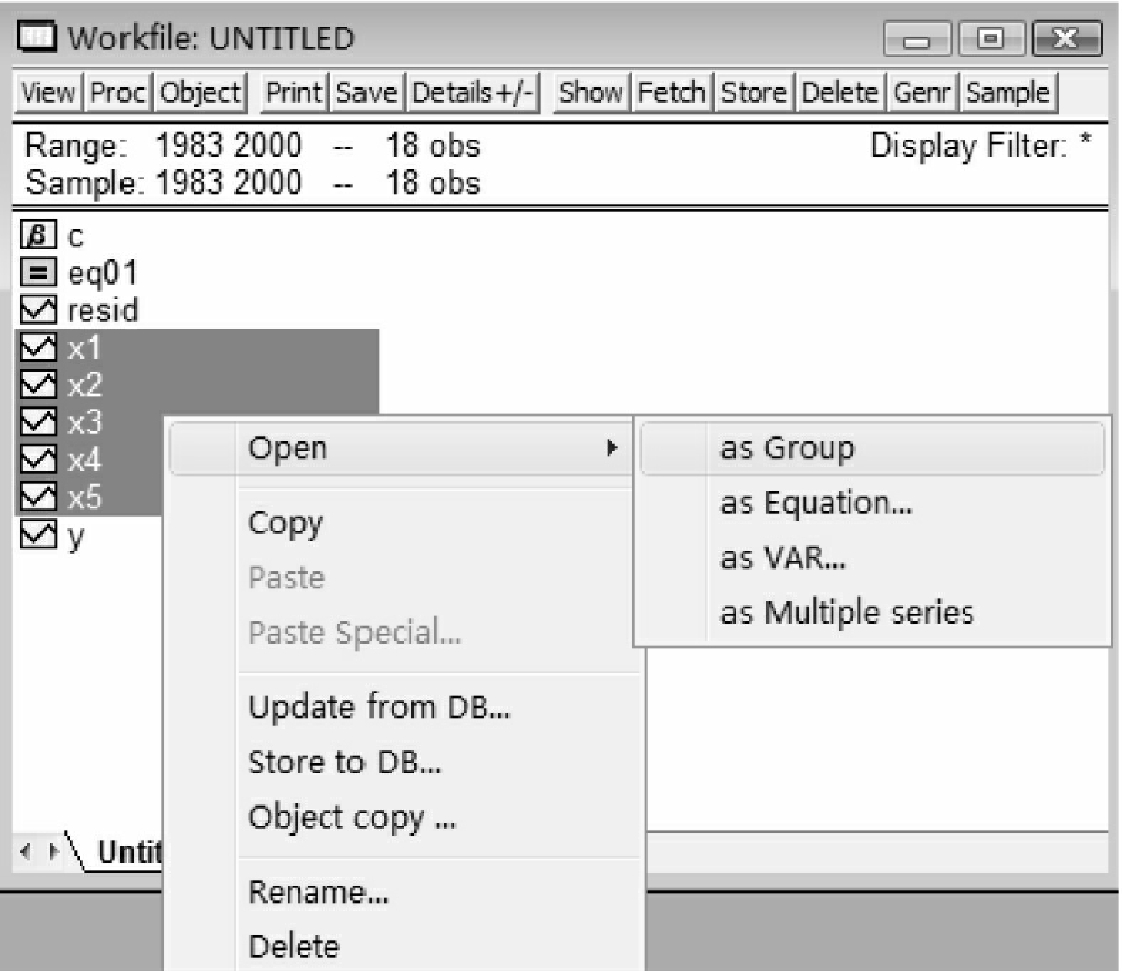
图5-2

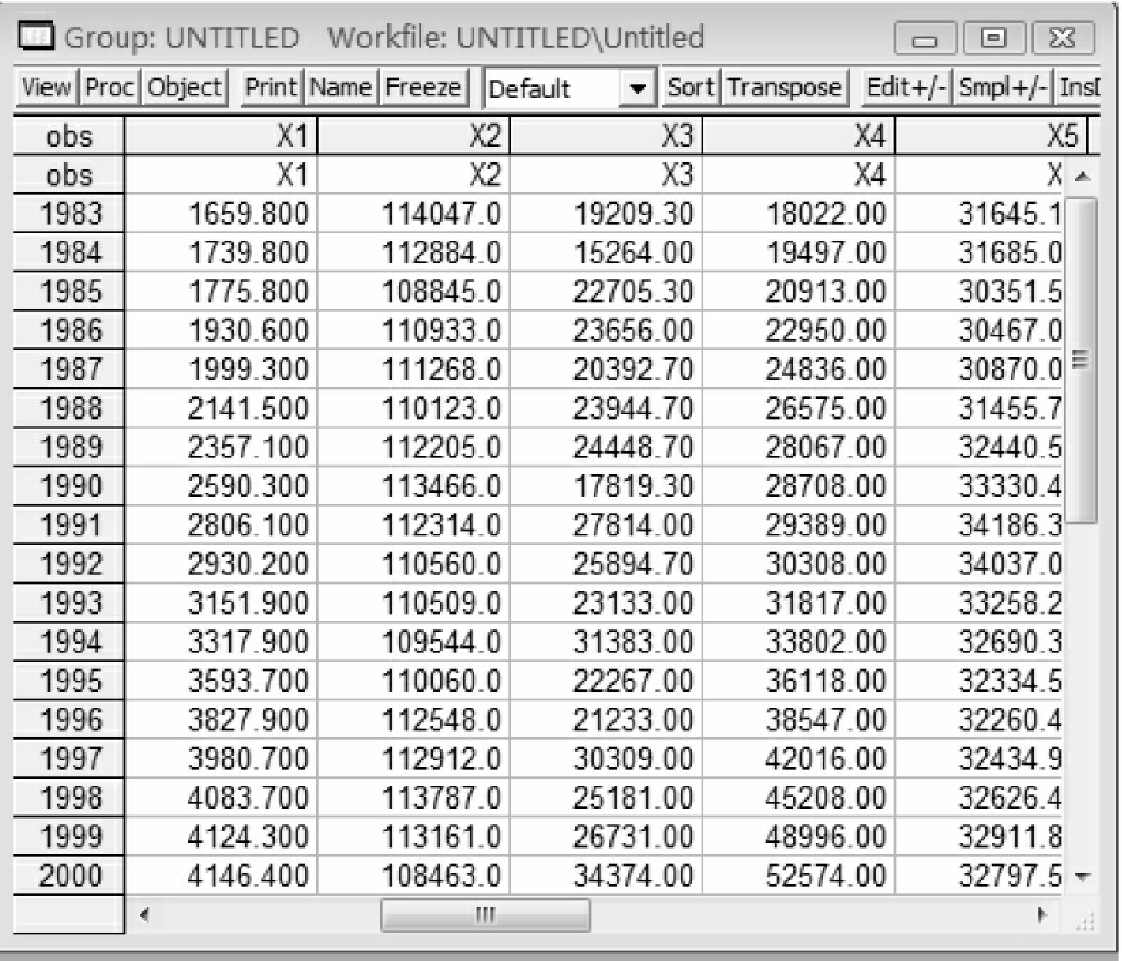
图5-3

图5-4

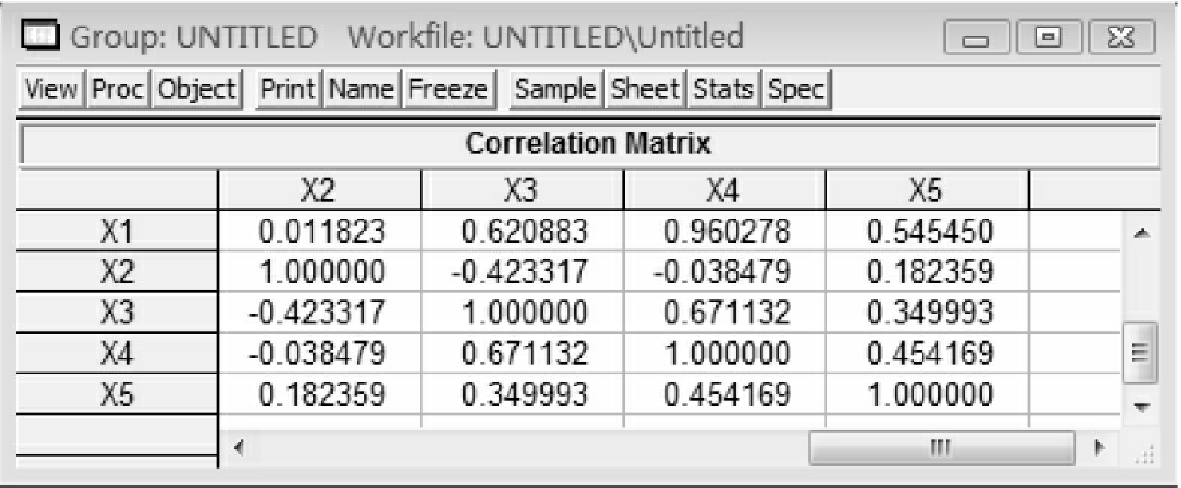
图5-5

参照例2-1，分别做y与x1，x2，x3，x4，x5间的回归，得到估计结果如图5-6～图5-10所示。

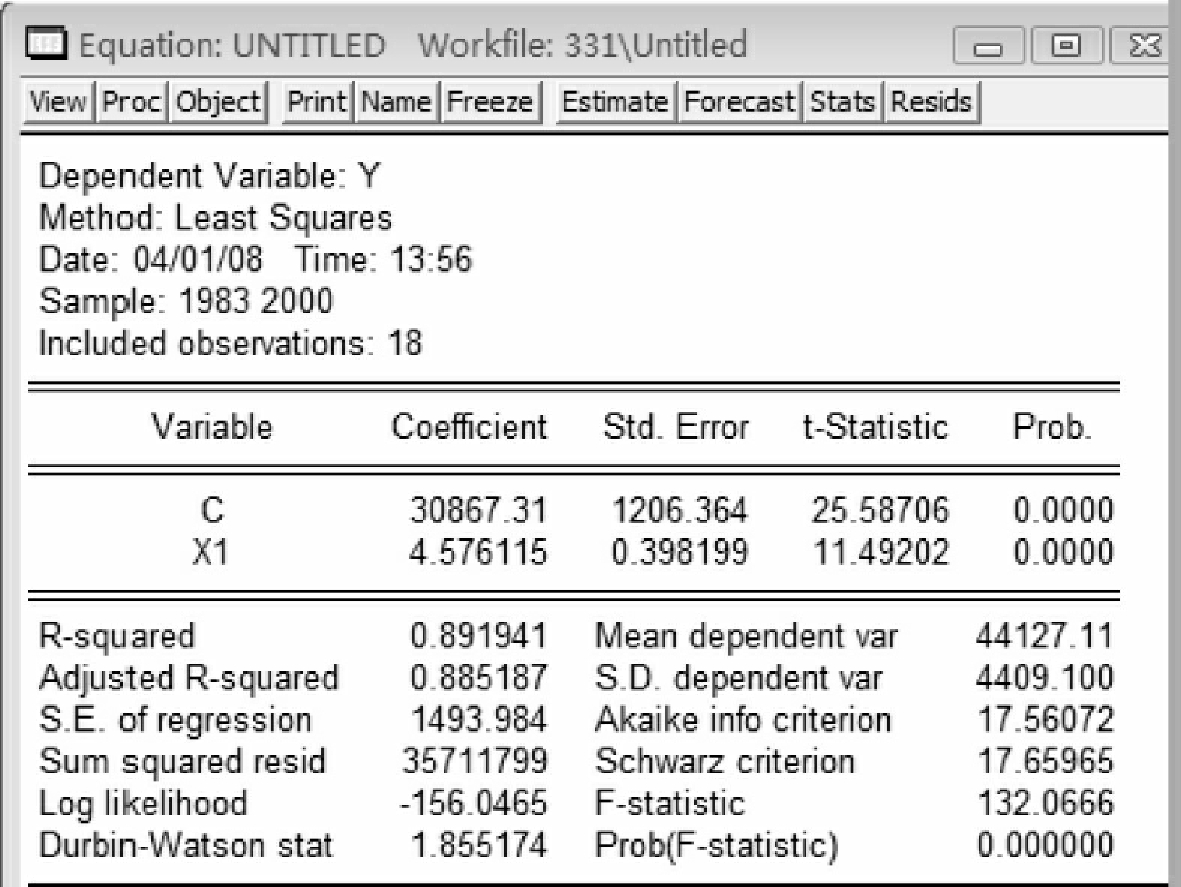
图5-6

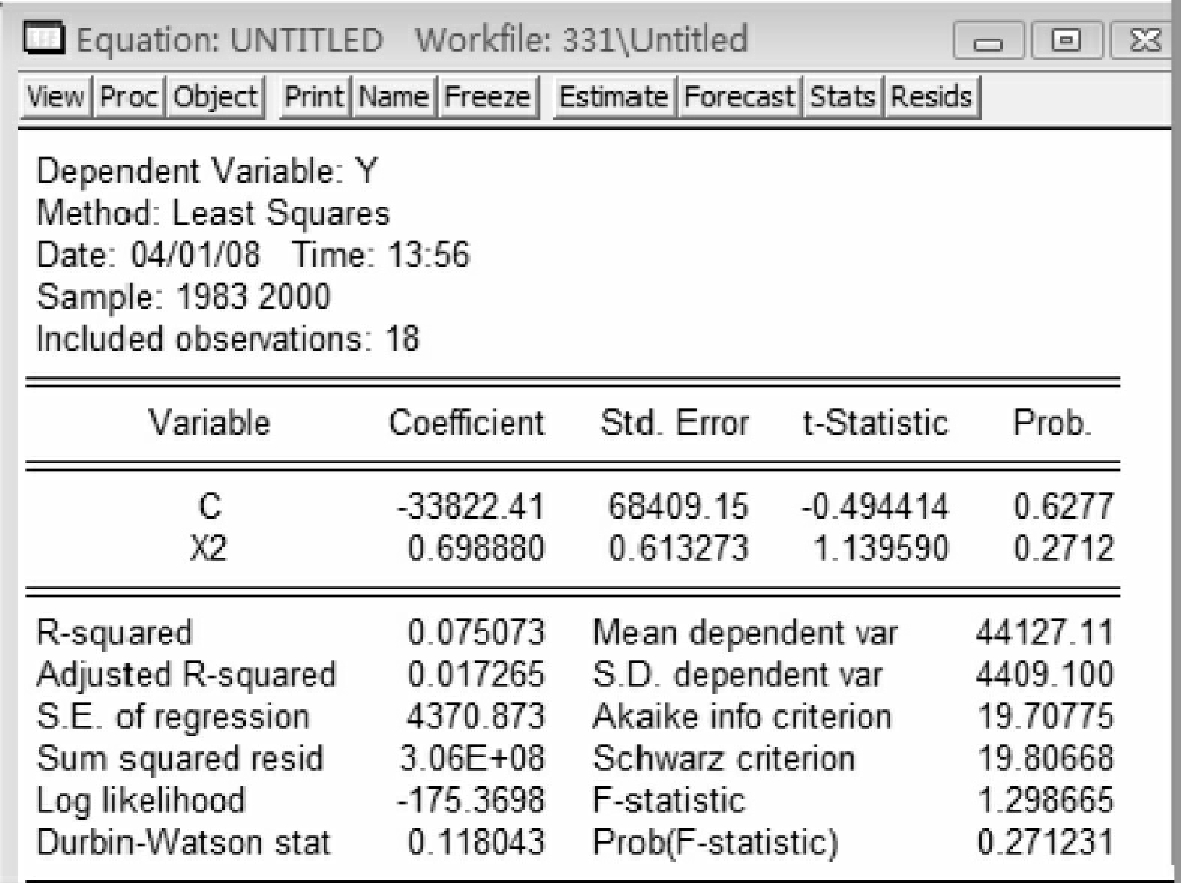
图5-7

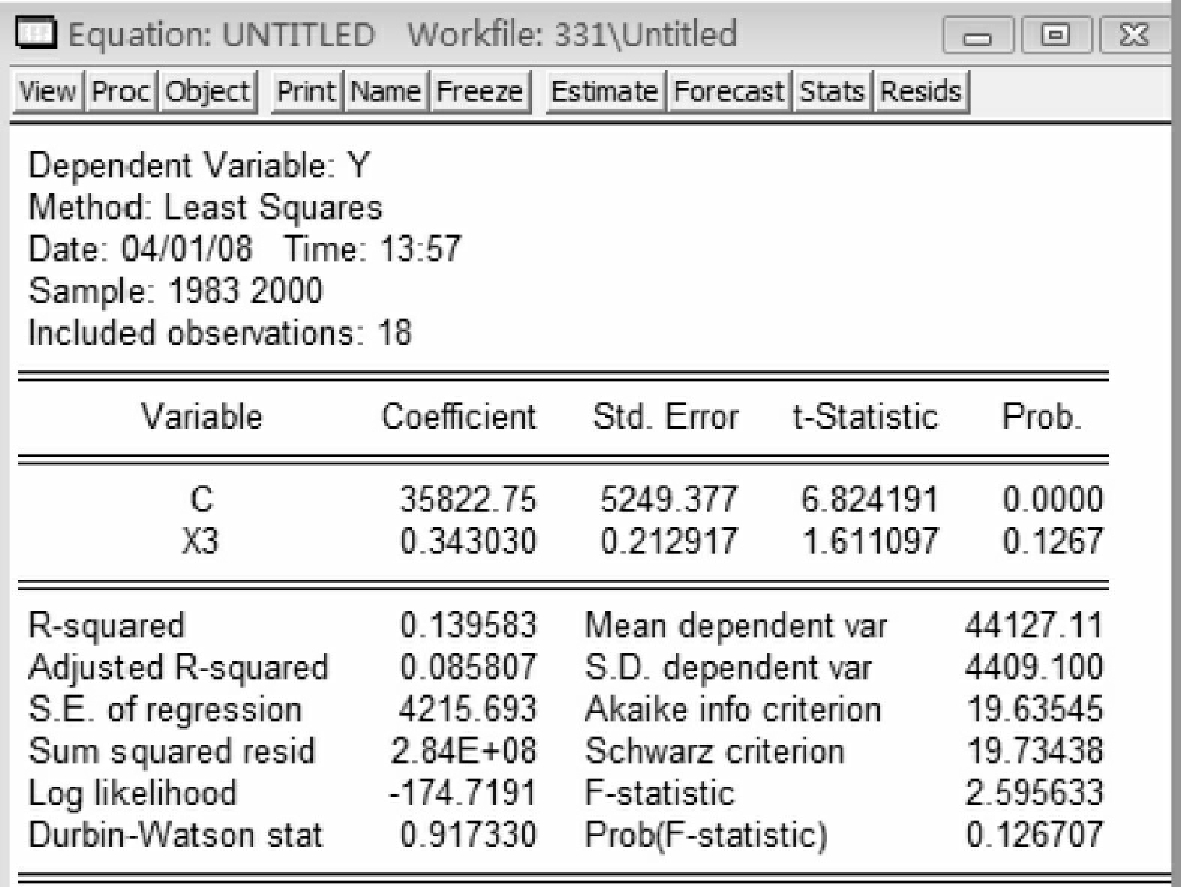
图5-8

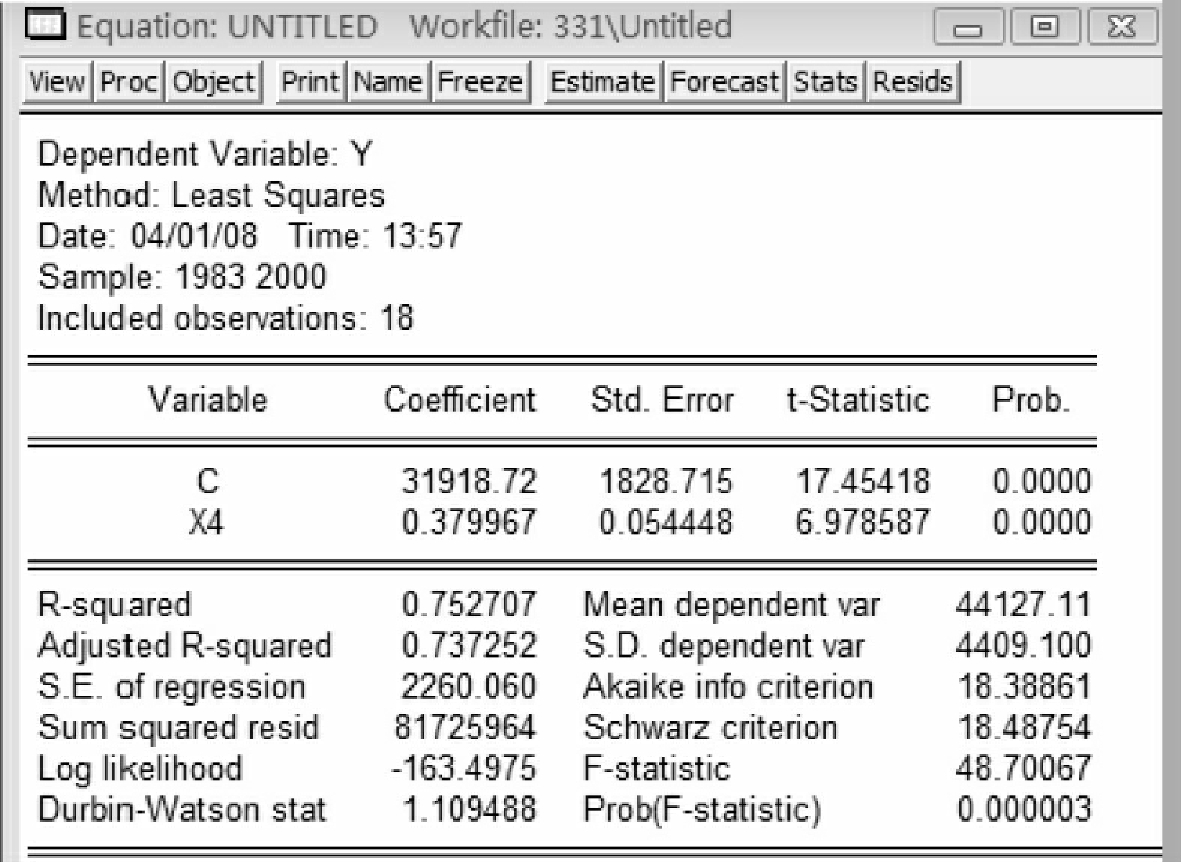
图5-9

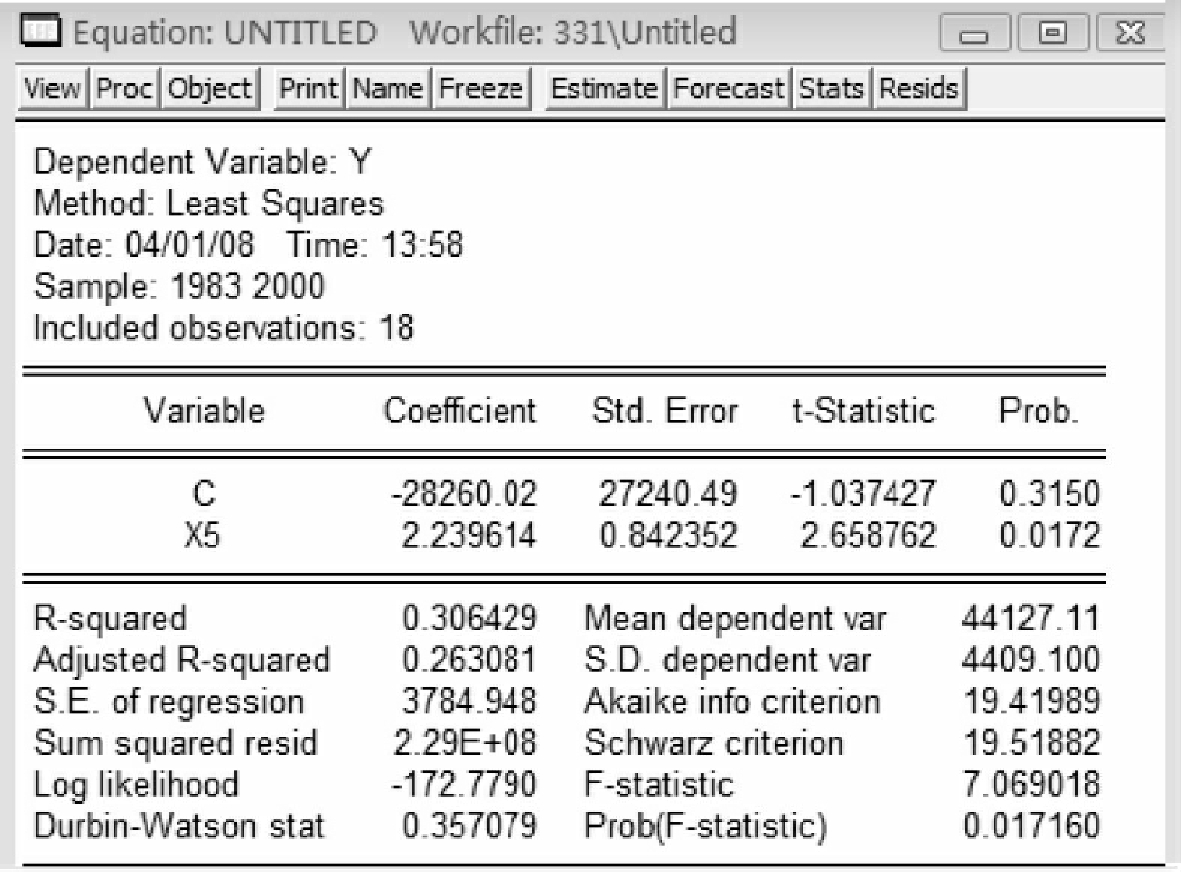
图5-10

从以上五个输出结果看，y用x1解释所得的回归方程拟合优度最高(R²= 0．89)，因此选择第一个方程作为基准的回归模型。即Y=30867．31062+ 4.576114592*X1(5-1)

第二步:在模型(5-1)初始方程的基准上，逐步将其他的解释变量加入进行回归，寻找拟合效果最好的回归方程。具体结果如下:

在模型(5-1)中添加了变量x2，在命令行中输入命令:ls y c x1 x2，得到图5-11。

观察可知，拟合优度显著提高(从R²=0．89提高到R²=0．96)，而且参数符号合理，t检验值也很显著，因此，将原模型(5-1)修改成下列模型:

Y=－43872．27229+4．561055211*X1+0．6704913829*X2(5-2)

在命令行中输入命令:ls y c x1 x2 x3，得到图5-12。

观察发现拟合优度高于前者，同时参数符号合理而且变量通过t检验。将模型(5-2)修改成:

Y=－12315．13841+5．264977937*X1+0．4155195658*X2－0．2130855455*X3

(5-3)

在命令行中输入命令:ls y c x1 x2 x3 x4，得到图5-13。

发现虽然拟合优度有所提高，但是变量x4前的符号不合理，而且P值=0．1205＞0．05，因此变量x4不显著。模型中剔除x4。

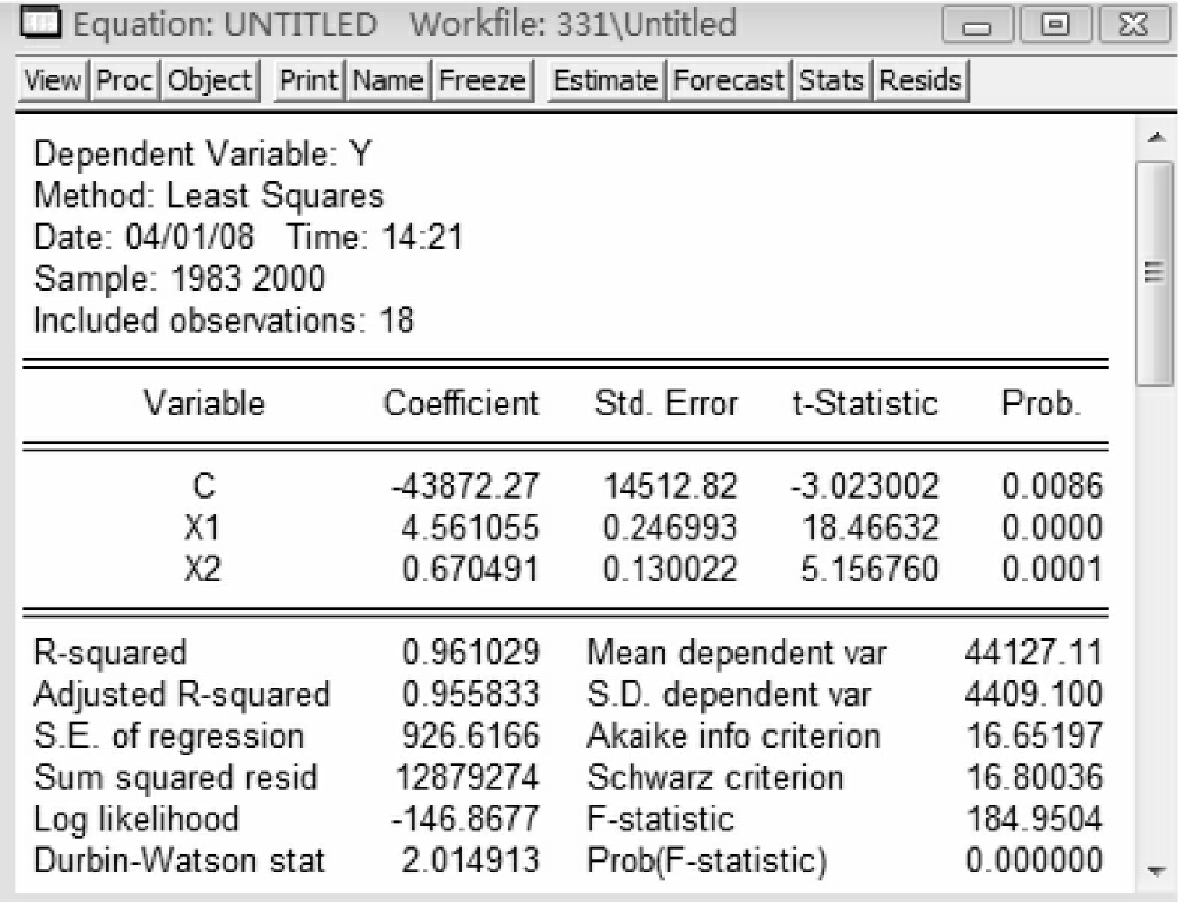
图5-11

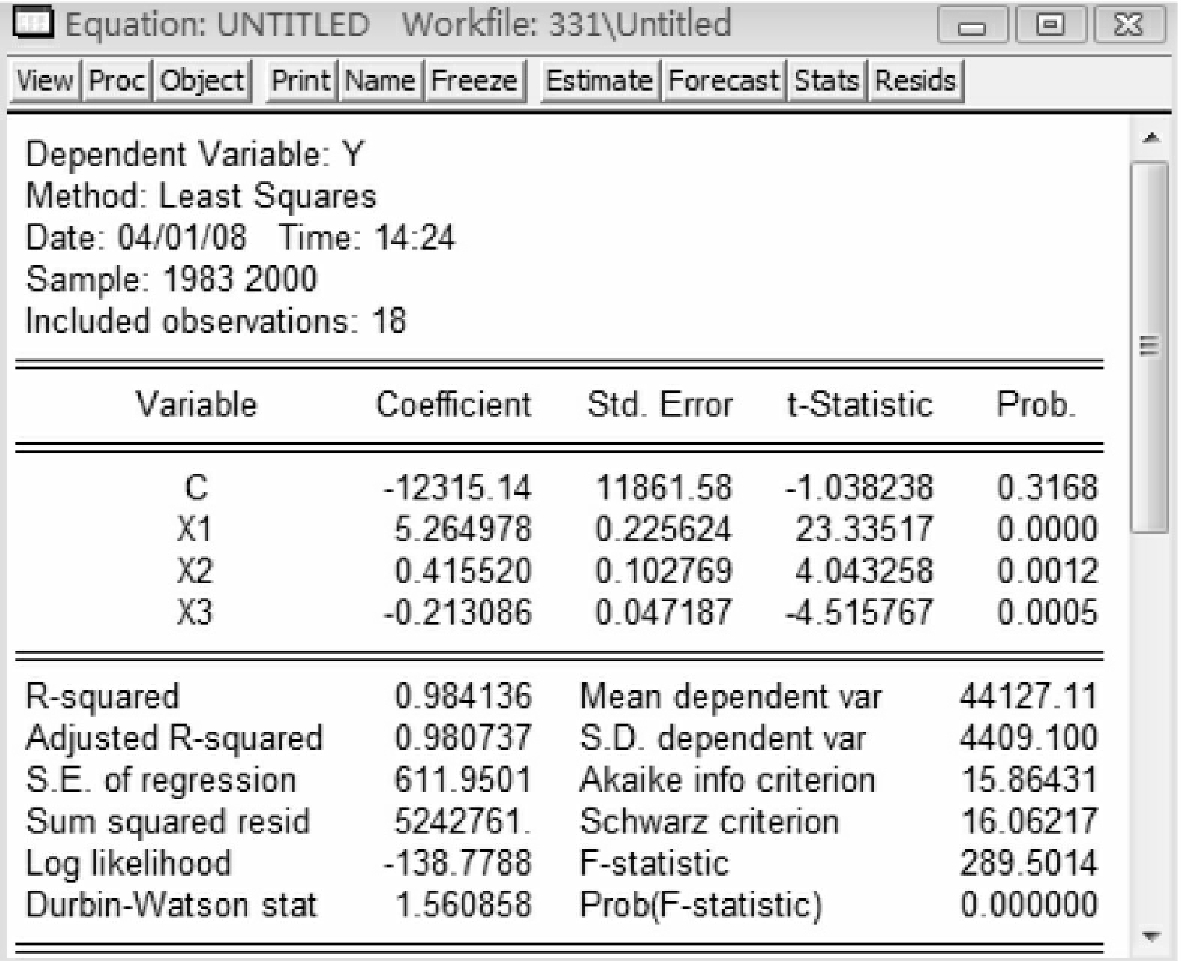
图5-12

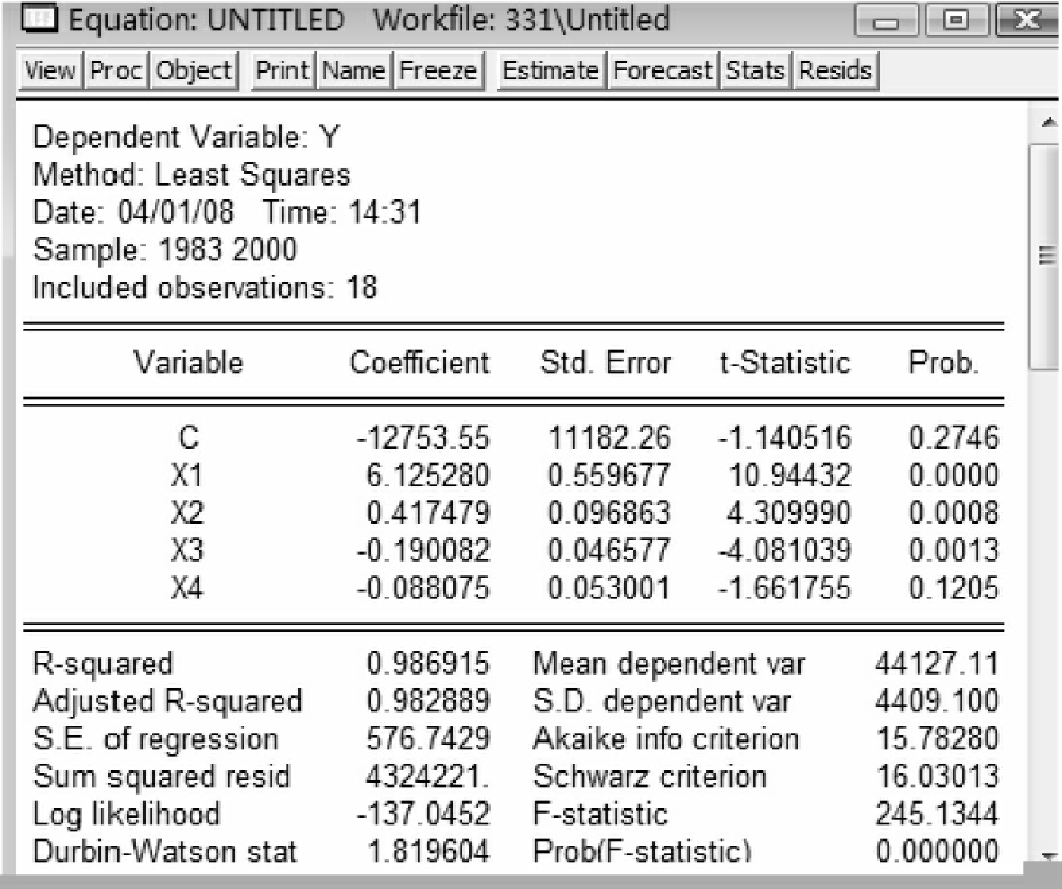
图5-13

在模型(5-3)中加入x5，估计可得图5-14。

图5-14

发现x5的参数t检验值并不显著，P值=0．6657＞0．05，因此模型中也剔除x5。此时，由于常数c的t检验值并不显著，剔除常数c，最终建立模型y=β₁x₁+β₂x₂+β₃x₃。输入命令:ls y x1 x2 x3，估计结果如图5-15所示。

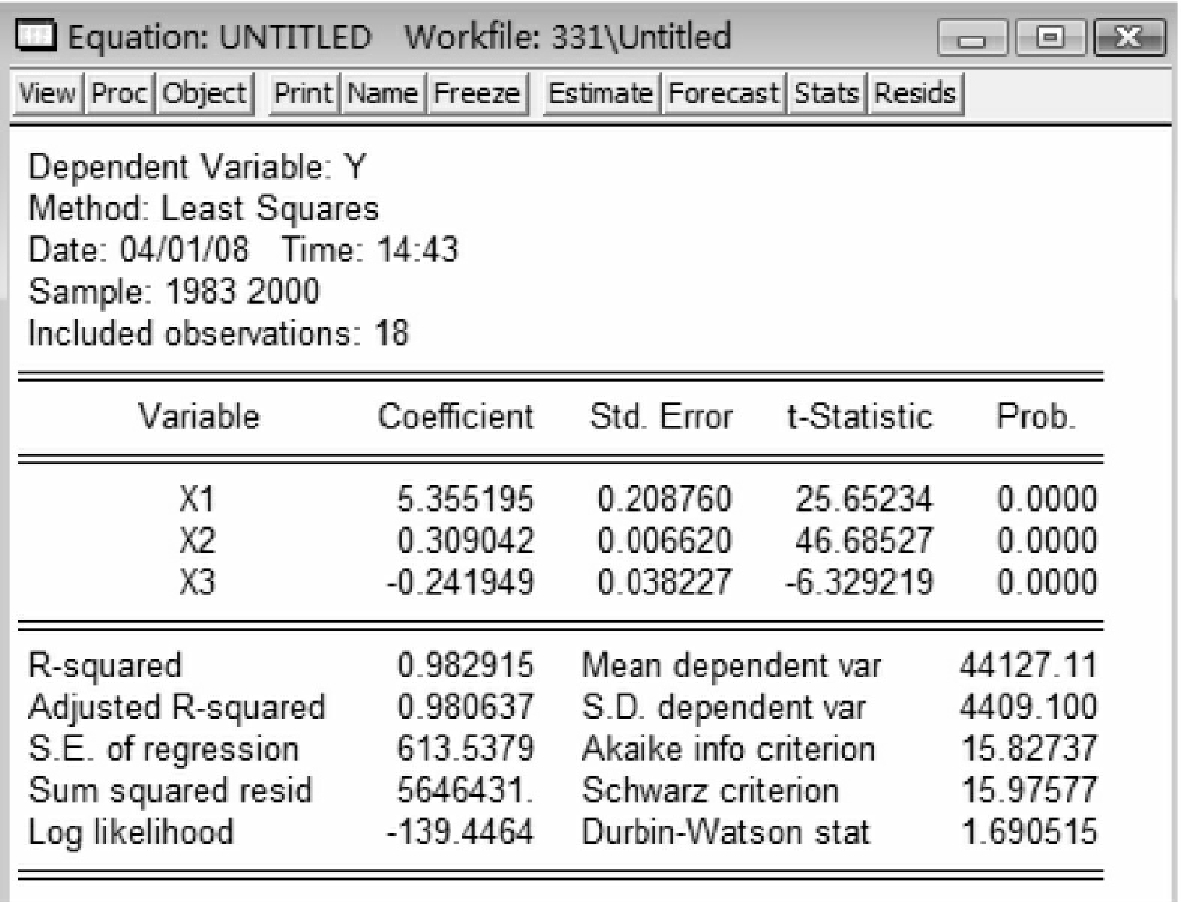
图5-15

估计方程为:

Y=5．355194889*X1

(25．65)+0．3090418342*X2(46．69)－0．2419486475*X3(－6．33)(5-4)

R²=0．98，所有的解释变量参数符号合理而且均通过t检验，因此，这时的估计方程(5-4)最好地拟合了数据。

(2)直接去除引起多重共线性的解释变量并对模型进行修正

如前所述，对模型y=β₀+β₁x₁+β₂x₂+β₃x₃+β₄x₄+β₅x₅估计得到图5-1。发现x4与x5参数检验并不显著，而方程的拟合度较高，因此，我们直接去掉农业机械总动力x4和农业劳动力x5这两个解释变量，从而对模型进行修正。

输入命令ls y c x1 x2 x3，估计得到图5-12。从中发现，常数项并不显著，剔除常数c，输入命令ls y x1 x2 x3，估计得到图5-15。此时得到拟合程度相对最好的方程(5-4)。