2.线性规划问题的模型
2.1引例
例3.6某工厂在计划期内要安排Ⅰ、Ⅱ两种产品的生产,已知生产单位产品所需的设备台时及A、B两种原材料的消耗、资源的限制,如表3.7。
表3.7
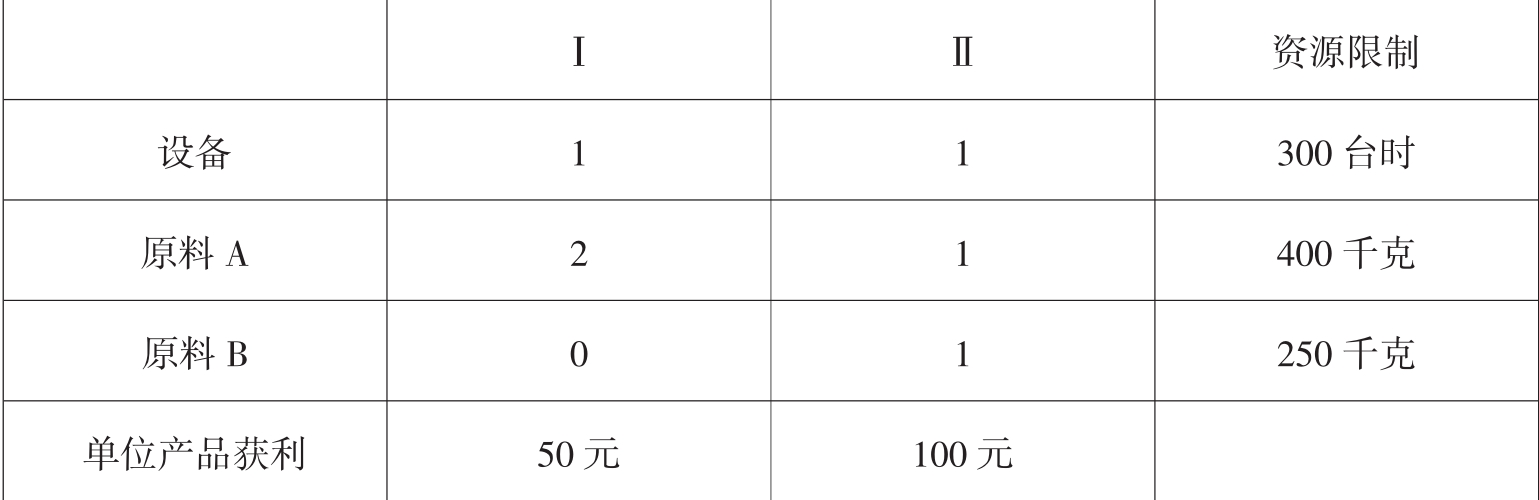
问题:工厂应分别生产多少单位Ⅰ、Ⅱ产品才能使工厂获利最多?线性规划模型:
目标函数:MaxZ=50x1+100x2
约束条件:s.t
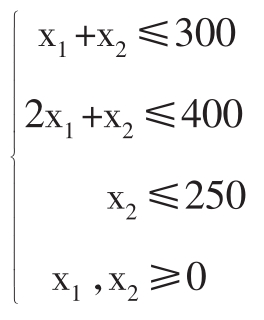
2.2线性规划模型的组成
①目标函数:MaxZ或MinZ
②约束条件:s.t.满足于
③决策变量:用符号来表示可控制的因素
2.3建模过程
①理解要解决的问题,了解解题的目标和条件;
②定义决策变量(x1,x2,…,xn),每一组值表示一个方案;
③用决策变量的线性函数形式写出目标函数,确定最大化或最小化目标;
④用一组决策变量的等式或不等式表示解决问题过程中必须遵循的约束条件。2.4一般形式
目标函数:Max(Min)Z=c1x1+c2x2+…+cnxn
约束条件:s.t.
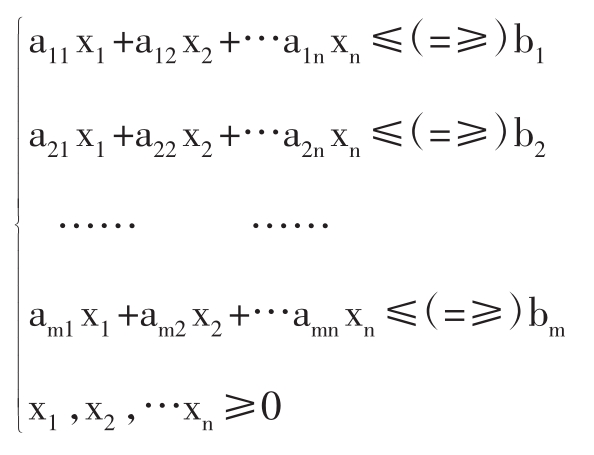
2.5线性规划问题的标准型
(1)线性规划问题的标准形式
目标函数
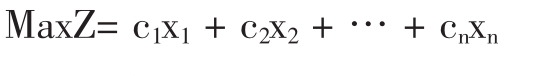
约束条件
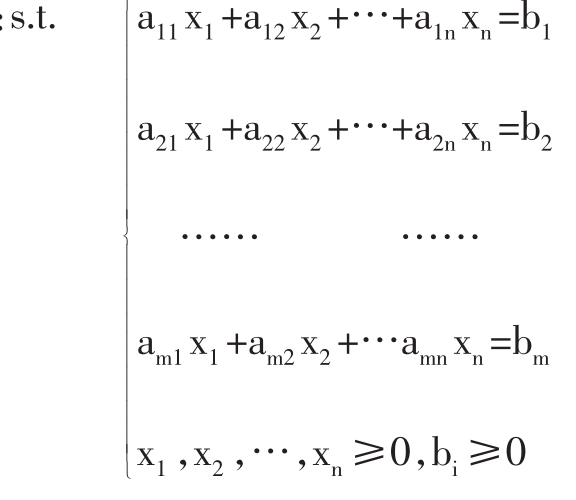
可以看出,线性规划的标准形式有如下四个特点:
①目标最大化;
②约束为等式;
③决策变量均非负;
④右端项非负。
(2)线性规划模型的标准化
对于各种非标准形式的线性规划问题,我们总可以通过以下变换,将其转化为标准形式。
①极小化目标函数的问题:
设目标函数为:Minf=c1x1+c2x2+…+cnxn
(可以)令z=-f,
则该极小化问题与下面的极大化问题有相同的最优解,
即MaxZ=-c1x1-c2x2-…-cnxn
但必须注意,尽管以上两个问题的最优解相同,但它们最优解的目标函数值却相差一个符号,即Minf=-Maxz。
②约束条件不是等式的问题:
设约束条件为:ai1x1+ai2x2+…+ainxn≤bi
可以引进一个新的变量s,使它等于约束右边与左边之差
s=bi–(ai1x1+ai2x2+…+ainxn)
显然,s也具有非负约束,即s≥0,
这时新的约束条件成为
ai1x1+ai2x2+…+ainxn+s=bi
当约束条件为:ai1x1+ai2x2+…+ainxn≥bi时,
类似地令s=(ai1x1+ai2x2+…+ainxn)-bi
显然,s也具有非负约束,即s≥0,这时新的约束条件成为
ai1x1+ai2x2+…+ainxn-s=bi
为了使约束由不等式成为等式而引进的变量s,当不等式为“小于等于”时称为“松弛变量”;当不等式为“大于等于”时称为“剩余变量”(也可以称为“松弛变量”)。如果原问题中有若干个非等式约束,则将其转化为标准形式时,必须对各个约束引进不同的松弛变量。
③右端项有负值的问题:
在标准形式中,要求右端项必须每一个分量非负。当某一个右端项系数为负时,如bi<0,则把该等式约束两端同时乘以-1,得到:-ai1x1-ai2x2-…-ainxn=-bi。
④决策变量的非负约束:
在标准形式中,必须每一个变量均有非负约束。当某一个变量xj≤0时,只需令xj′=-xj,则xj′≥0。
当某一个变量xj没有非负约束时,可以令xj=xj′-xj″,其中xj′≥0,xj″≥0,即用两个非负变量之差来表示一个无符号限制的变量,当然xj的符号取决于xj′和xj″的大小。
例3.7将以下线性规划问题转化为标准形式?
Minf=2x1-3x2+4x3
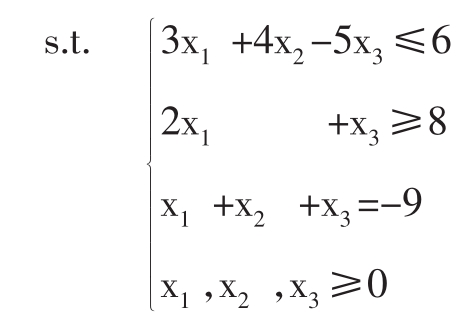
解:首先,将目标函数转换成极大化:令Z=-f=-2x1+3x2-4x3其次考虑约束,有2个不等式约束,引进松弛变量x4,x5≥0。第三个约束条件的右端值为负,在等式两边同时乘-1。通过以上变换,可以得到以下标准形式的线性规划问题:
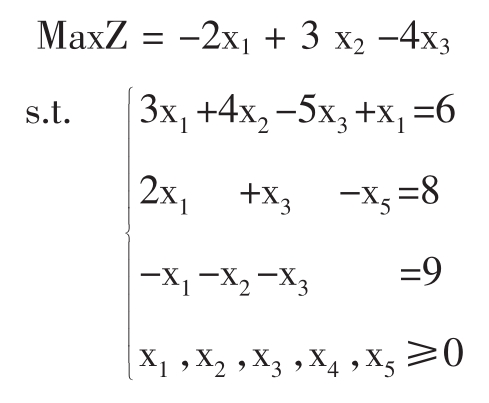
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















