短期成本理论

一、短期成本概念与分类

根据本章第一节可知，本教材使用的可变成本与固定成本都是从机会成本的角度来讨论的。在短期内，厂商的成本可以分为三类七种成本，相应地成本曲线也会有七条：

（一）短期总成本（short-run total costs，STC）

1.总固定成本（total fixed costs，TFC）

总固定成本TFC是指那些短期内无法改变的固定投入所带来的成本，这部分成本不随产量的变化而变化，又称不变成本。一般包括厂房和资本设备的折旧费、地租、利息、财产税、广告费、保险费、办公室雇员等项目支出。用来生产某一特定产品的这些投入成本，即使在企业停产的情况下，也必须支付，只有在企业完全倒闭时才会没有。所以它有时候也可以看作厂商的一种沉没成本。但是，如果厂商不生产时可以卖掉这些固定投入或出租给其他厂商使用并收取租金，那么，这样的固定成本则是一种机会成本。短期内进行生产决策时，理性的生产厂商不会考虑的部分，TFC=b。

2.总可变成本（total variable costs，TVC）

总可变成本TVC是指短期内可变投入的成本，它随产量的变化而变化。例如：原材料、燃料、动力支出、生产流水线雇员的工资等。当产量为零时，可变成本也为零，产量越多，可变成本也越多，TVC=φ（Q）。

3.短期总成本（short total costs，STC）

短期总成本STC是指厂商在短期内为生产一定数量的产品对全部生产要素所支付的最小总成本，它是总固定成本和总可变成本之和，即

（二）短期平均成本（short-run averge costs，SAC）

1.平均固定成本（averge fixed costs，AFC）

平均固定成本AFC是指厂商短期内平均生产每一单位产品所消耗的固定成本。在固定成本不变的情况下，随着产量的增加，分摊到每一单位产品量上的固定成本是减少的，因此平均固定成本是越来越小的。平均固定成本用公式表示为：

2.平均可变成本（averge variable costs，AVC ）

平均可变成本AVC是指厂商短期内生产平均每一单位产品所消耗的总变动成本。在生产的初期，平均可变成本随着产量的增加而不断下降；当产量增加到一定量时，平均可变成本达到最小；而后随着产量的继续增加平均可变成本开始增加。平均可变成本用公式表示为：

3.短期平均总成本（short averge costs，SAC）

短期平均总成本SAC是指厂商短期内平均生产每一单位产品所消耗的全部成本，它由短期平均固定成本和平均可变成本构成。在生产的初期，随着产量的增加，平均总成本不断下降；产量增加到一定量时，平均总成本达到最小；而后随着产量的继续增加，平均总成本开始增加。平均总成本用公式表示为：

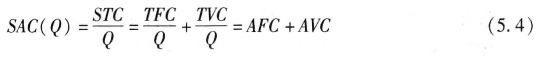
（三）短期边际成本（short marginal cost，SMC）

短期边际成本在这里是指厂商在短期内增加一单位产量所引起的总成本的增加。在生产的初期，随着产量的增加，边际成本不断下降；产量增加到一定量时，边际成本达到最小；而后随着产量的继续增加，边际成本开始增加。短期边际成本用公式表示为：

当△Q→0，函数连续、可导时：

二、短期成本函数

成本函数实际上就是在生产函数的基础上，引入生产要素价格，进一步用来讨论最低投入与产出之间相互关系的一个范畴。引入要素价格以后，投入方就变成了生产成本（即要素数量乘以相应的要素价格），而产出方仍然是产品数量。那么成本函数就表示在一定时期内，技术水平和投入要素价格不变的条件下，生产过程中投入的最低成本与产出量之间确定性的相互关系。成本函数是以产出量作为自变量的函数：C=f（Q）。上一章我们已经定义了短期，可以由厂商的短期生产函数推导出相应的短期成本函数，并在短期成本前加“S”。

短期生产函数它表示在资本投入量K固定不变的条件下，劳动的最低投入量L和产出量Q之间存在着相互依存的对应关系，厂商可以通过对劳动数量的改变来调整产出量；反过来，厂商也可以根据产出量来相应地确定劳动的投入量。Q是L的函数，根据反函数的定义，有L是Q的函数，L=L（Q）。

短期总成本STC是指短期内生产一定量产品所需要的最低成本总和。短期投入分为固定投入和可变投入。相应地，短期成本也分为固定成本与可变成本。如果用w表示劳动的价格，用r表示资本的价格，那么短期总成本就等于劳动价格乘以劳动数量加上资本价格乘以资本数量，即STC=w·L（Q）+r·K。由于在短期中资本数量不随着产量的变动而变动，r·K应为一常数，所以，短期成本函数的一般形式可以写为：

式中： φ（Q）表示可变成本，它随着产量的变动而变动；b表示固定成本，为大于0的常数。

三、短期成本曲线

（一）三种短期总成本曲线

总固定成本、总可变成本、总成本曲线形状及相互关系的一般形式^[3]可以用图5-1说明，图中横轴代表自变量产量Q，纵坐标代表因变量成本C。总固定成本TFC与产量Q的变化无关，所以总固定成本曲线是一条平行于横轴的水平线。总可变成本TVC随着产量的变化而变化，产量为零时可变成本为零，产量增加可变成本增加，所以总可变成本曲线是一条从原点出发，向右上方倾斜的曲线，在拐点前都是先以递减的斜率上升，在拐点后以递增的斜率上升。总成本是固定成本与可变成本之和，并且由于固定成本是一常数，所以总成本曲线的变动规律与可变成本的变动规律相似：在拐点前都是先以递减的斜率上升，在拐点后以递增的斜率上升。不同的是，TVC的起点是原点，而STC的起点是TFC与纵坐标的交点。在任一产量水平的STC与TVC之间的垂直距离都相等，都是等于TFC。

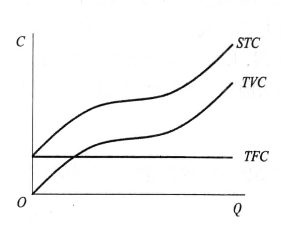
图5-1　STC、TFC、TVC曲线

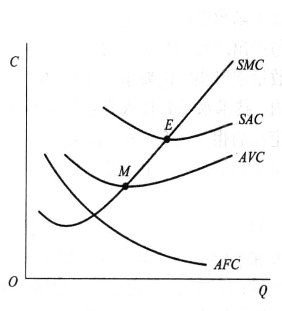
图5-2　AFC、AVC、SAC、SMC曲线

（二）三种短期平均成本曲线

不同厂商的平均成本可能会不同，相应地，不同厂商就有不同的AFC、AVC及AC图形。但一般而言，短期平均固定成本、平均可变成本、平均成本曲线形状及相互关系可以用图5-2说明。图中横轴代表自变量产量Q，纵坐标代表因变量成本C。平均固定成本AFC曲线是一条向右下方倾斜的曲线，随产量的增加，AFC一直呈下降趋势。由于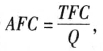为直角双曲线的一支，随Q增加，AFC递减并向横轴渐近，但不会与横坐标相交，这是因为短期中总固定成本不会为零。平均可变成本AVC曲线是一条U型曲线，随着产量的增加，平均可变成本减少，减少到一定程度后，达到平均可变成本曲线的最低点，而后随着产量的进一步增加，平均可变成本开始上升。平均成本SAC曲线也是一条U型曲线，随着产量的增加，曲线先下降再上升。第四章的图4-11已经对此进行了说明。这里SAC与AVC的变动规律相同，但它们之间有两点不同须特别注意：第一，SAC一定在AVC的上方，两者差别在于垂直距离永远为AFC。当Q无穷大时，SAC与AVC无限接近，但永不重合，不相交。第二，SAC与AVC最低点不在同一个产量上，而是SAC最低点对应的产量较大。即A VC已经达到最低点并开始上升时，SAC仍在继续下降，原因在于AFC是不断下降的，只要AVC上升的数量小于AFC下降的数量，SAC就仍在下降。

（三）短期边际成本曲线

如图5-2，短期边际成本曲线也是一条U型曲线，随着产量的增加，初期边际成本迅速下降，很快降至最低点，尔后迅速上升，同一产量点上其斜率递增的速度快于AVC、SAC。由于STC=TFC+TVC，而TFC始终不变，因此SMC的变动与TFC无关，SMC实际上等于每增加额外一单位产量所引起的可变成本的增加量。即：

SAC、AVC、AFC和SMC四条成本曲线以及它们之间的关系如图5-2所示。SAC、AVC、SMC曲线都是U型曲线。SAC曲线在AVC曲线的上方，它们之间的距离相当于AFC，而且SMC曲线与AVC曲线、SAC曲线相交于AVC曲线、SAC曲线的最低点，即M、E点。最后需要指出的是，各种成本曲线的形状之所以会呈现出以上特点，仍然与生产中“投入—产出”的特点有关，从生产论到成本论，仅仅只是引入了生产要素价格，而生产要素价格在产品市场的分析中，它只是个外生变量，不会引起生产特点的变化，所以支配短期成本曲线形状的规律仍然是边际报酬递减规律。

四、短期成本变动的决定因素——边际报酬递减规律

如第四章所述，边际报酬递减规律是短期生产中的一个基本规律，这一规律同样适用于短期成本分析。成本分析与生产函数分析不同之处是成本分析中用的是价值量概念，而生产分析中用的是实物量概念。现在假定生产要素的价格不变，来分析边际报酬递减规律在短期成本分析中的体现。我们从产量变化所引起的边际成本变化的角度来理解这一规律。如图4-2所示，在边际报酬递增阶段，增加一单位可变要素投入所产生的边际产量递增，则意味着可以反过来说：在这一阶段增加一单位产量所需要的要素投入是递减的，所以要素数量乘以相应的要素价格以后得到的边际成本也是递减的。在以后的边际报酬递减阶段，增加一单位可变要素投入所产生的边际产量递减，则意味着在这一阶段增加一单位产量所需要的要素投入是递增的，所以要素数量乘以相应的要素价格以后得到的边际成本也是递增的。

短期生产论中把生产要素投入作为自变量，产出作为因变量，而成本论中把产出作为了自变量，生产要素投入作为了因变量，所以在边际报酬递减规律作用下的短期边际产量和短期边际成本之间存在着一定的对应关系：在短期生产中，由于边际报酬呈递减规律，边际产量的递增阶段对应的是边际成本的递减阶段，边际产量的递减阶段对应的是边际成本的递增阶段，与边际产量的最大值相对应的是边际成本的最小值。

正因为如此，这就决定了短期边际成本SMC曲线呈U形特征，从而也决定了其他短期成本曲线的特征以及短期成本曲线之间的相互关系。

第一，关于SMC曲线的形状。短期生产开始时，由于边际报酬递增的作用，增加一单位可变要素投入所生产的边际产量是递增的；反过来，增加一单位产量所需的边际成本是递减的。当可变要素投入超过一定界限后，增加一单位可变要素投入所生产的边际产量是递减的；反过来，每增加一单位产量所需要的边际成本是递增的。因此，在边际报酬递减规律作用下，SMC曲线先递减后递增，最终形成一条U形曲线。

第二，关于STC曲线和TVC曲线的形状。考虑到STC曲线和TVC曲线的形状完全相同，在此仅就STC曲线的形状进行分析。SMC曲线在边际报酬递减规律作用下先降后升，而SMC又是STC曲线上相应点的斜率，因此，STC曲线的斜率也是先递减后递增的，即STC曲线的斜率先递减后递增。SMC曲线的最低点则对应STC曲线上斜率由递减向递增变化的拐点。

第三，关于SAC、AVC曲线的形状。根据边际产量和平均产量之间的关系，当边际产量小于平均产量时，边际产量就向下带动平均产量，使得平均产量下降；当边际量大于平均产量时，边际产量就向上带动平均产量，使得平均产量上升；当边际产量等于平均产量时，平均产量达到本身的极点值。随可变要素投入数量的增加，SMC先减小，则相应的SAC也减小；随着可变要素投入数量的进一步增加，SMC开始增加，但小于SAC的数值，则SAC继续减少；当SMC继续增加，且SMC大于SAC时，SAC也开始增加。因此，在边际报酬递减规律作用下，SAC曲线也呈U形，但SAC曲线的最低点晚于SMC曲线的最低点出现。这是因为SMC曲线经过最低点开始上升时，由于SMC小于SAC，SAC曲线仍在下降。同样的道理也适用于AVC曲线，但是AVC曲线的最低点比SAC曲线的最低点先出现，并且前者位置也低于后者。这是因为在平均总成本中不仅有平均可变成本还有平均固定成本，正是由于平均固定成本的作用，才使得SAC曲线与AVC曲线的最低点出现的快慢、位置的高低都不同。

五、短期中产量函数与成本函数之间的对应关系

我们已经认识了短期生产中的边际报酬递减规律决定了短期产量曲线的特征，也决定了短期成本曲线的特征，现进一步分析短期生产条件下的生产函数与成本函数之间的对应关系。

假定短期生产函数为：

短期成本函数为：STC（Q）=TVC（Q）+TFC

TVC（Q）=w· L（Q）（劳动的价格w是既定的）

（一）边际产量与边际成本之间的关系

由SMC的定义得：

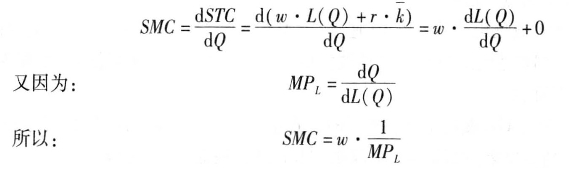
由上式可以得到两点结论：

第一，SMC与MPL成反比关系。由于MPL曲线先上升，然后下降，所以SMC曲线先下降，然后上升；且SMC曲线的最低点对应MPL曲线的最高点，如图5-3中的（a）图与（b）图所示。

第二，生产函数与成本函数存在对偶关系。当TPL曲线下凹时，STC曲线和TVC曲线上凸；当TPL曲线上凸时，STC曲线和TVC曲线下凹；TPL曲线上的拐点对应STC曲线和TVC曲线上的拐点，如图5-3中的（c）图与（d）图所示。

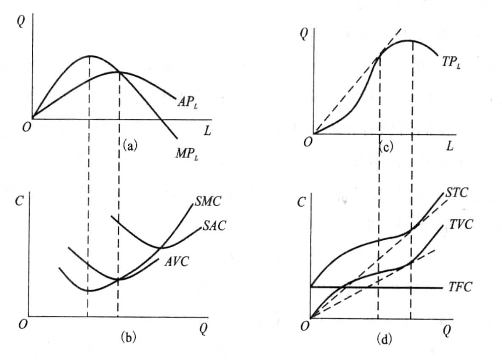
图5-3　短期生产函数与短期成本函数之间的对应关系

（二）平均产量与平均可变成本之间的关系

由AVC的定义得：

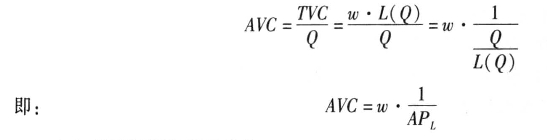
由上式可以得到两点结论：

第一，APL与AVC成反比关系。当APL递减时，AVC增加；当APL增加时，AVC减少；当APL达到最大值时，AVC达到最小值，APL曲线的最高点对应AVC曲线的最低点，如图5-3中的（a）图与（b）图所示。

第二，SMC曲线与AVC曲线相交于AVC的最低点。由于产量曲线中MPL曲线与APL曲线在APL曲线的最高点相交，所以SMC曲线在AVC曲线的最低点与其相交。

六、由短期总成本曲线推导平均成本曲线和边际成本曲线

以上讨论了七种短期成本曲线及其基本特征。现根据以上各种短期成本的定义，由短期总成本（STC、TFC、TVC）曲线出发，用几何方法推导出相应的短期平均成本（SAC、AFC、AVC）和短期边际成本（SMC）曲线，并从几何推导过程中，分析不同类型的短期成本曲线之间的相互关系。

（一）由短期总成本曲线推导短期平均成本曲线

1.由TFC曲线推导AFC曲线

可由图5-4说明。由于AFC（Q）=TFC/Q，所以，TFC曲线上任意一点与原点的连线的斜率，都是该产量上的AFC值。在图（a）中，当产量水平是Q1时，平均固定成本为Oa的斜率，即AFC1=TFC/Q1，我们可以在图（b）中找到相应的a′一点；当产量水平是Q2时，SAFC2=STFC/Q2，我们可以在图（b）中找到相应的b′一点；当产量水平是Q3时，AFC3=TFC/Q3，我们可以在图（b）中找到相应的c′一点；随着产量的增加，平均不变成本AFC是不断下降的，在图（b）中的AFC曲线是一条向右下方倾斜并以横轴为渐近线的曲线。

2.由TVC曲线推导A VC曲线

可由图5-5说明。因为AVC （ Q）=TVC/Q，所以，连接TVC曲线上任何一点与原点的线段的斜率就是该产量水平上相应的AVC值。在图（a）中连接a、b、c三点与原点，得到了三条直线Oa、Ob、Oc，这三条直线的斜率值就是产量水平为Q1、Q2和Q3时相应的AVC的值。其中，在产量水平为Q2时，一条经过原点的直线与TVC相切于b点，并且，在所有的TVC曲线上的点与原点的连线中，这一条直线的斜率是最小的，这说明产量水平为Q2时A VC的值是最小的。在TVC曲线的b点之前，随着产量的增加，TVC曲线上的点与原点的连线斜率越来越小，相应的AVC会越来越小；到达b点时达到最小；过了b点以后，随着产量的增加，TVC曲线上的点与原点的连线斜率又开始越来越大，相应的AVC会越来越大。图（b）是根据图（a）绘制的AVC曲线，随着产量的增加，AVC曲线呈现先下降后上升的U形；在产量为Q2时，相应的AVC曲线的b′点达到最小值。

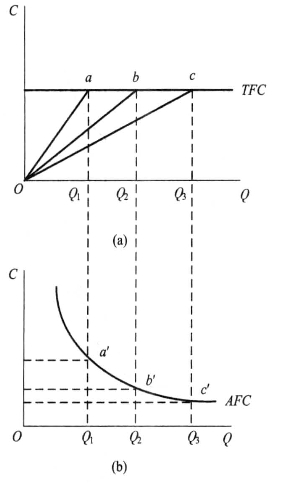
图5-4　由TFC曲线推导AFC曲线

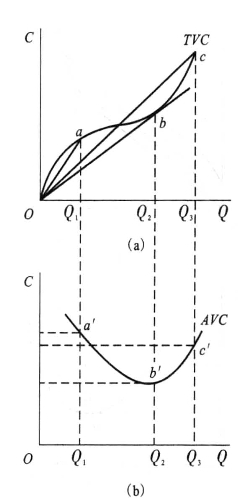
图5-5　由TVC曲线推导AVC曲线

3.由STC曲线推导SAC曲线

可由图5-6说明。因为SAC（Q）=STC/Q，所以，连接STC曲线上任何一点与原点的线段的斜率就是该产量上相应的SAC值。这个推导过程与上面由TVC曲线推导AVC曲线的过程是类似的。在图（a）中，产量水平Q1、Q2和Q3上的SAC值分别为Oa、Ob和Oc的斜率值，其中在b点的时候，Ob的斜率值是在所有的STC曲线上的点与原点的连线中最小的。在b点之前，随着产量的增加，斜率值是递减的；在b点之后，随着产量的增加，斜率值是递增的。与此相对应的，在图（b）中，SAC曲线呈现先下降后上升的U形，在产量为Q2，相应的SAC曲线的b′点达到最小值。

（二）由总成本曲线推导边际成本曲线

由STC曲线和STVC曲线推导SMC曲线，可由图5-7说明。因为SMC （ Q）=dSTC/dQ=dTVC/dQ，所以，任何产量水平上的SMC值既可以由STC曲线又可以由STVC曲线上的相应的点的斜率给出。在图5-7（a）中STC和STVC曲线都是先以递减的斜率上升，后以递增的斜率上升，在图5-7（b）中得到的SMC曲线就是先下降后上升的U形，并且在产量为Q1时，图5-7（a）中STC曲线的拐点a点，与图5-7（b）中SMC曲线的最低点a′是对应的。

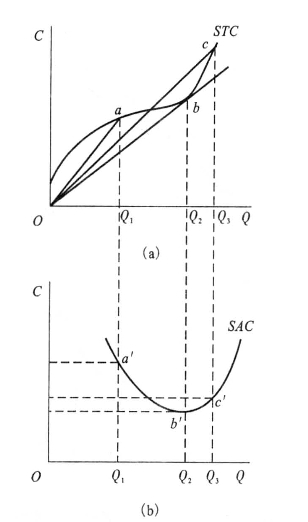
图5-6　由STC曲线推导SAC曲线

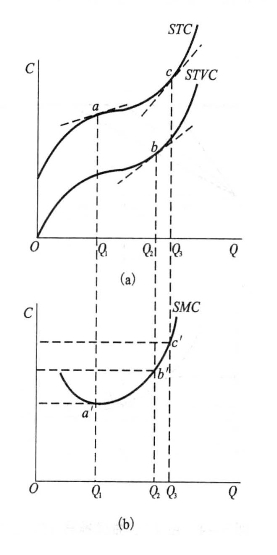
图5-7　由STC、TVC曲线推导SMC曲线