【摘要】：在实际应用中，知识表达系统的数据通常以数据关系表的形式表示。数据关系表的行对应要研究的对象，列对应对象的属性，对象的信息是通过对象的各属性值来表达。IND＝｛（x，y）∈U×U｜a∈B，f（x，a）＝f（y，a）｝等价关系IND，构成了U的一个划分，用U/IND＝｛γ1，γ2，…，γn｝表示，其中γi表示不同的等价类，在IND下与γ不可分辨的所有对象构成一个等价类，记为［γ］IND。
3.2 标准粗糙集理论介绍
下面给出标准粗糙集理论中的知识表达系统、二元等价关系、正域等概念。
定义3－1 四元组S＝（U，A，V，f）是一个知识表达系统［127］，其中：U表示对象的非空有限集合，称为论域；A表示所有属性的非空有限集合；V＝
，Va表示属性a的值域；f表示U×A→V的信息函数，它为每个对象的每个属性赋予一个信息值。
在实际应用中，知识表达系统的数据通常以数据关系表的形式表示。数据关系表的行对应要研究的对象，列对应对象的属性，对象的信息是通过对象的各属性值来表达。
定义3－2 每一个属性子集B≤A决定了一个二元等价关系IND（B）［132］，即
IND（B）＝｛（x，y）∈U×U｜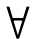
a∈B，f（x，a）＝f（y，a）｝等价关系IND（B），
构成了U的一个划分，用U/IND（B）＝｛γ1，γ2，…，γn｝表示，其中γi表示不同的等价类，在IND（B）下与γ不可分辨的所有对象构成一个等价类，记为［γ］IND（B）。
定义3－3 对于知识表达系统S＝（U，A，V，f），设
，γ∈U，称－B［γ］＝｛γ∈U｜［γ］IND（B）＞γ｝和B［γ］＝｛γ∈U｜［γ］IND（B）∩γ＝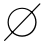
｝分别为γ关于IND（B）的上近似和下近似［127］。而POSR（γ）＝－B［γ］称为γ的R正域，NEGR（γ）＝U－
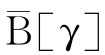称为γ的R负域，BND（γ）＝
－
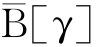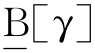称为γ的边界域。
正域是由那些根据知识R判断肯定属于γ的U中对象组成的集合；负域是由那些根据知识R判断肯定不属于γ的U中对象组成的集合；边界域是由那些根据知识R判断可能属于γ的U中对象组成的集合。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
