可变精度粗糙集模型介绍

3.3　可变精度粗糙集模型介绍

3.3.1　可变精度粗糙集模型

粗糙集理论（Rough Set Theory，RST）是波兰学者Pawlak Z于1982年提出的一种数据分析理论^［127］，是一种刻画不完整性和不确定性的数学工具，能有效地分析和处理不精确、不一致、不完整等各种不完备信息，并从中发现隐含的知识，揭示潜在的规律。该理论与统计方法、模糊方法、论据理论等其他处理不确定性问题的方法相比，最显著的特点是无需处理数据关系表之外的任何先验信息。此外，RST是一种非线性的平行处理结构模式，能对相关性指标进行约简，并进一步提取决策规则。

然而，来源于现实的数据集合大多存在着数据的不确定性或不完整性。由于RST对数据的要求过于严格，导致存在一些不足之处，主要体现在：缺乏对噪声数据的适应能力，抗干扰能力差；分类只有严格的“包含”和“不包含”，缺乏柔性或鲁棒性；大部分决策系统的属性之间并不一定存在严格的函数依赖关系，而只是表现出近似依赖的关系；对于边缘区域，不能区分等价类与集合的重叠度，没有体现程度上的差别等。

为了增强RST的抗干扰能力，Ziarko于1993年将RST扩展成VPRS^［128］。VPRS与RST不同，它是考虑了一定置信水平下的分类分析，是RST的一种重要推广。VPRS主要分析决策系统各属性间统计意义上的数据模式，或者存在概率上的不确定关系时的分类问题，而不是严格意义上的属性函数依赖关系，增强了RST的数据分析能力。

VPRS通过设置精度系数或包含度β，放宽了RST对边界的严格定义，柔化了边界。通常β的取值有两种方式，Ziarko把β定义为分类误差率^［128］，其取值范围为［0.0，0.5］；而An等则定义β为分类正确率［129］，其取值范围为（0.5，1.0］。本书采用An等的定义，设定β的取值范围为（0.5，1.0］。

与RST相类似，VPRS中也定义了β正域、β负域、β边界域^［130］。设U为论域，表示对象的非空有限集合；C表示所有条件属性的非空有限集合。集合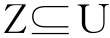和的β正域、β负域和β边界域为

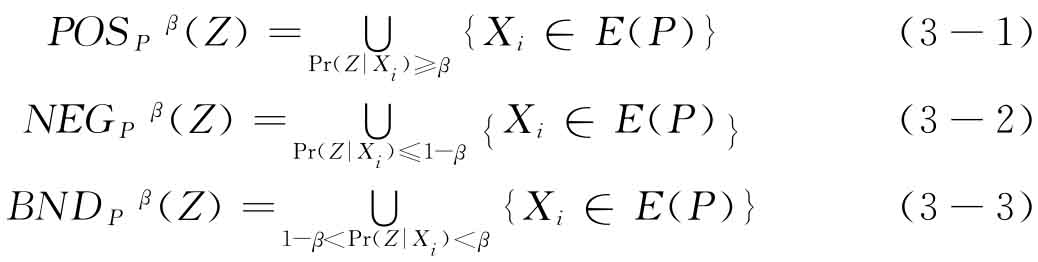
式中，E（P）是P的子集的条件分类，描述了一类等价类。式（3－1）中的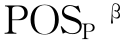（Z）表示根据等价关系将U中的元素正确分类的概率超过β的等价类的集合；式（3－2）中的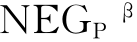（Z）表示根据等价关系将U中的元素误分类的概率不超过1－β的等价类的集合；式（3－3）中的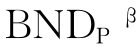（Z）是两者之差。当β＝1时，VPRS和RST是一致的，即VPRS是RST的一种扩展。

对于决策系统S＝（U，C∪D），U为论域，C为条件属性集，D为决策属性集，β＝（0.5，1.0］。在RST下，一旦给定决策系统，正域即确定，分类率（依赖度）则可计算确定。对于VPRS而言，分类率与包含度β值紧密相关。在VPRS中Ziarko^［130］将分类率定义为

其中，对于给定的β值而言，Z∈E（P）和P∈C。γ^β（P，D）是RST分类率的推广，描述了在一个给定的β值下，论域U中基于决策类能被确定分类的对象比率，即所有决策类β正域中对象的个数与整个论域中的对象个数之比。当β＝1时，它即为RST分类率γ（P，D）。

然而，对于分类而言，并非所有的条件属性都是必要的，为此VPRS引进属性的β约简。对于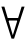a∈C，如果满足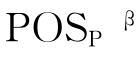（Z）＝（Z），则a是冗余属性，称C′＝C－｛a｝为C的一个β约简。C的所有β约简为RED^β（C，D）。求解属性约简的算法有很多，包括遗传算法^［131］、扩展法则^［132］和动态约简^［133］等。而一个约简的有效性可用约简的支持度来描述，约简的支持度越大则越有效。

在β约简的基础上可以进一步得到决策规则。

设RED是RED^β（C，D）中的一个约简，U/R（RED）＝｛X₁，X₂，…，X_n｝，则一等价类X_i的描述Des（X_i）可用下式表示：

式（3－5）中的∩表示交算子，x_j表示等价类X_i中的一个元素。

类似地，Y的描述Des（Y）可表示为：

式（3－6）中d是一决策属性，且x_j∈Y。这样，RED对应的决策规则就可以用下式来表示：

3.3.2　规则价值衡量方法

在一个决策表中，条件属性与决策属性之间的因果关系可以表示为粗糙决策规则，从数据中发现这种规则，正是粗糙集数据分析的目标。从系统客观层面评价一条规则主要依据可信度、覆盖率和支持数3个指标来衡量^［134］。对于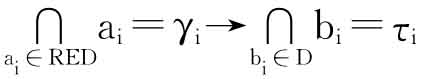这一规则，简记为α→β，可信度acc（α→β）、覆盖率cov（α→β）、支持数sup（α→β）由下式给出

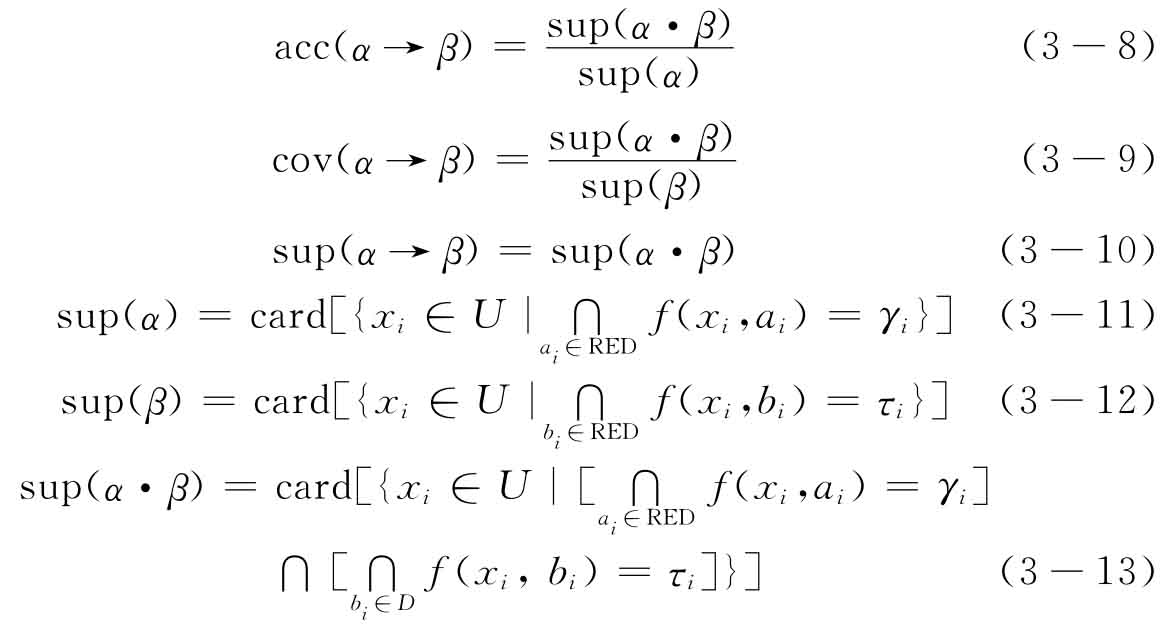
其中的card（·）指集合的基。

直观地讲，可信度表示运用该规则进行推理正确的概率；覆盖率表示该规则的支持数在相应决策类中的比重；支持数表示在论域中支持该规则的元素个数。