基于偏差最大化的多属性决策方法的提出

4.3　基于偏差最大化的多属性决策方法的提出

对于属性权重完全未知，属性值为不确定语言变量的MADM问题，关键之一是确定属性权重。MADM问题一般是对方案属性值的排序比较。若所有方案在属性u_j下的属性值差异越小，则说明该属性对方案决策与排序的作用越小；反之，如果属性u_j能使所有方案的属性值有较大差异，则说明其对方案决策与排序将起重要作用。因此，从对方案进行排序的角度考虑，方案属性值偏差越大的属性应该赋予越大的权重。特别地，若所有方案在属性u_j下的属性值无差异，则属性u_j对方案排序将不起作用，此时可令其权重为零。对于u_j，用D_ij（ω）表示方案x_i与其他所有方案的偏差，用定义4－2中的偏离度表示：

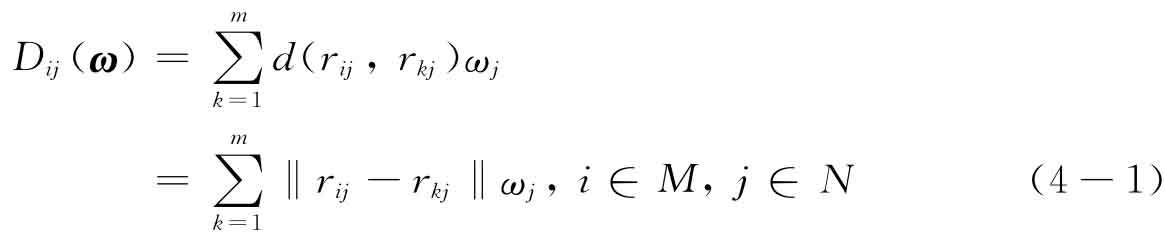
式中，r_ij表示决策者关于方案x_i在属性u_j下的不确定语言变量评估。

式中，D_j（ω）表示对于属性u_j而言所有方案与其他方案的总偏差。

依据上述分析，属性权重向量ω的选择应使所有属性对所有方案的总偏差最大。为此，构造偏差函数

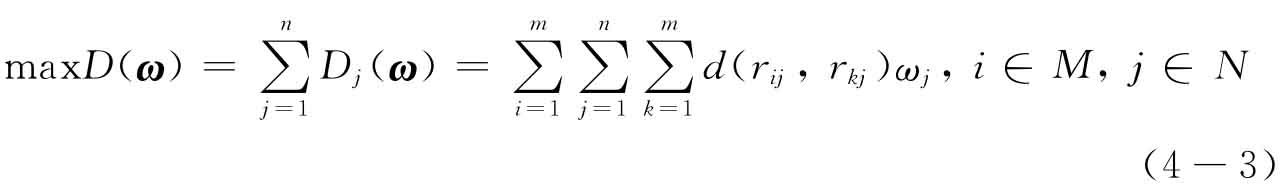
进一步构建目标规划问题：

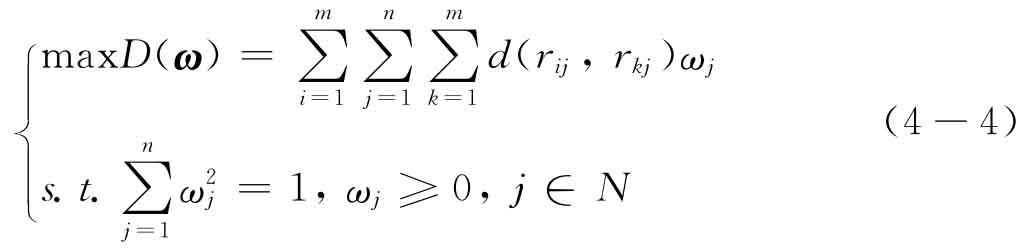
解此最优化模型：作拉格朗日（Lagrange）函数

求得最优解

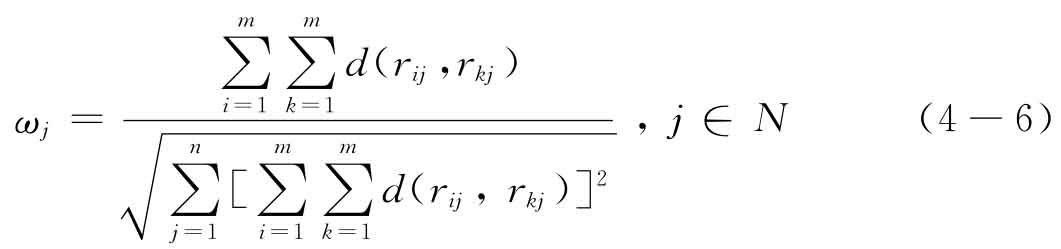
对上述权重向量作归一化处理，可得

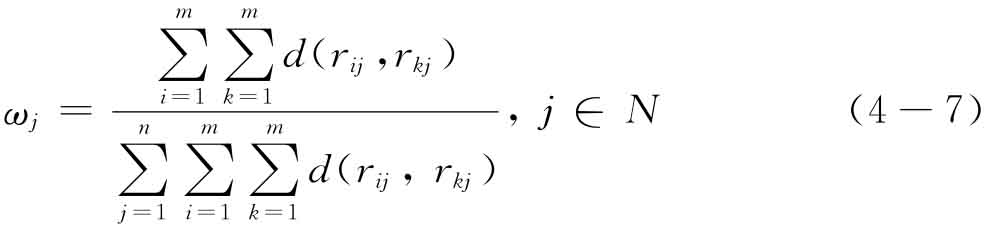
式（4－7）的意义在于通过运用不确定语言变量的偏离度把已知的客观决策信息反映出来，且易于计算未知的属性权重。

对于已知的不确定语言评估矩阵R＝（r_ij）_m×n，其中r_ij为不确定语言变量，表示方案x_i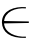X关于属性u_j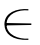U下的不确定语言变量评估，而各属性的权重由式（4－7）给出。结合前文给出的ULWA算子，方案x_i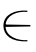X的评估值z_i（ω）表示为：

显然，方案x_i的评估值z_i（ω）越大，则方案x_i越优。由于各方案的评估值z_i（ω）仍是不确定语言变量，不能直接对方案进行排序。因此，下面将提出基于期望－方差的不确定语言变量的排序方法。

对于处理不确定语言评估信息的MADM问题，在选择决策方案过程中，一般需要对不确定语言变量进行比较和排序。现有的排序方法在文献［148］中已有介绍：首先计算不确定语言变量两两之间的可能度，并建立相应的可能度矩阵；然后求出基于可能度矩阵的排序向量，并按其大小对不确定语言变量进行比较和排序。从该方法的计算过程来看，该方法计算量大，过程复杂。鉴于此，本章试图定义不确定语言变量的期望和方差，引入期望－方差方法对不确定语言变量进行排序。

首先，将不确定语言变量s看作［s_a，s_b］上服从均匀分布的随机变量。下面将给出不确定语言变量的期望和方差定义。

定义4－5　设s是［s_a，s_b］上的不确定语言变量，s的期望和方差为

其次，定义基于期望－方差的两个不确定语言变量间的优先序。

定义4－6　设s＝［s_a，s_b］和s′＝［s_a′，s_b′］是不确定语言变量，s优于s′当且仅当下列两种情形之一发生：

①E（s）＞E（s′）；

②E（s）＝E（s′）且σ（s）＜σ（s′），记作ss′。

定义4－7　设s＝［s_a，s_b］和s′＝［s_a′，s_b′］是不确定语言变量，s等价于s′当且仅当E（s）＝E（s′）且σ（s）＝σ（s′），记作s～s′。

定义4－8　设s＝［s_a，s_b］和s′＝［s_a′，s_b′］是不确定语言变量，s劣于s′，当且仅当下列两种情形之一发生：

①E（s）＜E（s′）；

②E（s）＝E（s′）且σ（s）＞σ（s′），记作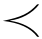ss′。

最后，应用定义4－6至定义4－8对方案进行排序，确定最优的方案。

下面归纳总结出一类属性权重完全未知、属性值为不确定语言变量MADM问题的决策方法的具体步骤，见图4－1。

步骤1　根据实际情况设定合适的语言评估标度，并将其量化；

步骤2　在量化后的语言评估标度下，决策者给出方案x_i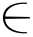X关于属性u_jU下的不确定语言变量评估r_ij，并得到评估矩阵R＝（r_ij）_m×n；

步骤3　应用式（4－7）计算此类MADM问题的权重ω_j；

步骤4　应用式（4－8）计算各方案的评估值z_i（ω）；

步骤5　应用定义4－5计算各方案评估值z_i（ω）的均值和方差；

步骤6　应用定义4－6至定义4－8对方案进行排序，并选择最优方案。

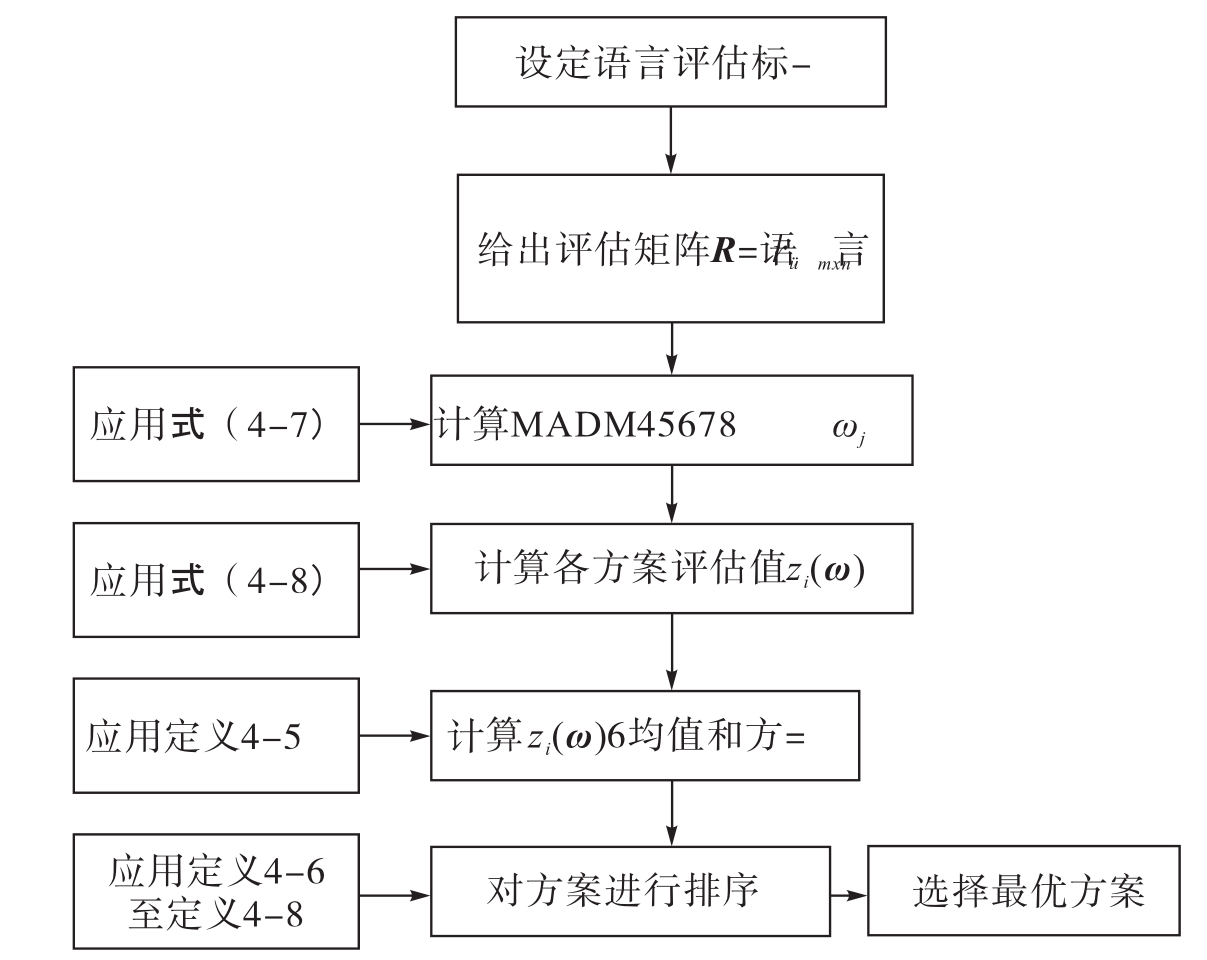
图4－1　决策步骤