风险效用函数度量法

3.3.6　风险效用函数度量法

风险效用函数如图3-7所示，效用理论用效用函数来描述项目群决策者的风险偏好，项目群风险偏好包括四种类型:风险回避(Risk Aversion)、风险中性(Risk Neutral)、风险喜好(Risk Seeking)、风险偏好一般(Risk General)。

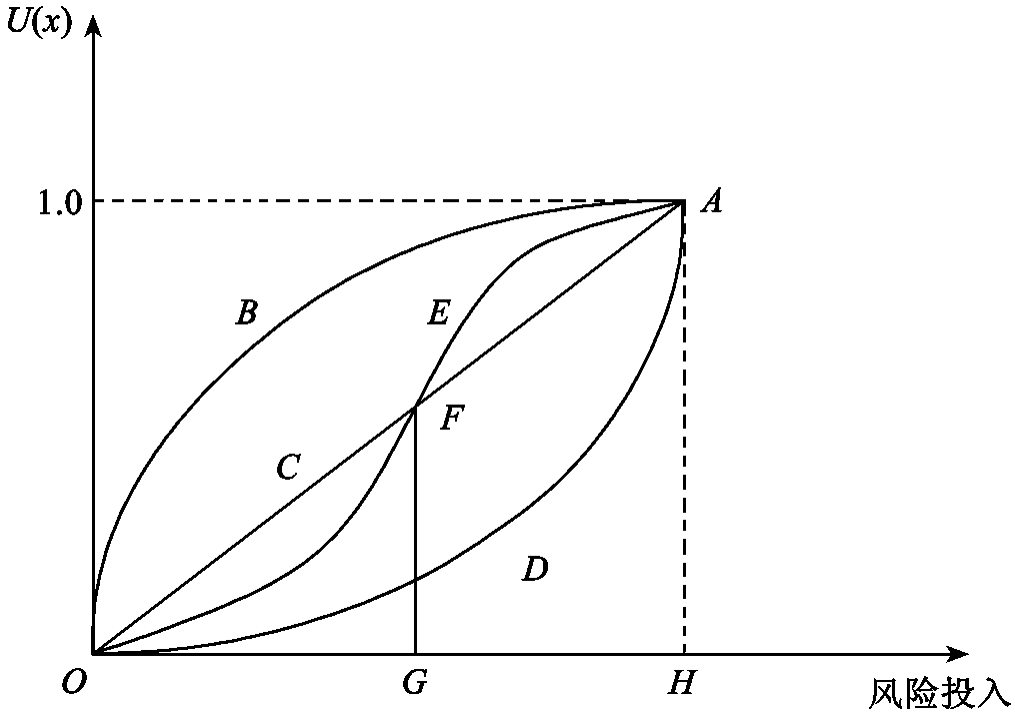
图3-7　风险效用函数曲线

(1)风险回避。在图3-7中，曲线B对应的是凸函数，随着损益值的增加，效益也相应增加，递减的速度在逐渐降低，有U'(x)＞0，U″(x)＜0，表明项目群决策者对于亏损敏感，对高收益不是很感兴趣。Krzystofowicz研究发现，在风险效用函数曲线中，风险效用函数和价值函数存在非线性的指数函数关系，其函数表达式为

U(x)=a_o+bexp(－c－x)，(b＞0，c＞0)　　(3.15)

(2)风险中性。在图3-7中，曲线C对应的是直线，有U'(x)＞0，U″(x)＜0，表明项目群决策者对于亏损敏感，对高收益不是很感兴趣。根据Allains和Sarin主观效用函数与价值函数之间的关系，其函数表达式为

U(x)=a_o+b(x)，(b＞0)　　(3.16)

(3)风险喜好。在图3-7中，曲线D对应的是凹函数，随着损益值的增加，效益也相应增加，递增的速度在逐渐增加，有U'(x)＞0，U″(x)＞0，表明项目群决策者专注于获得较大利益，对亏损不敏感，其函数表达式为

U(x)=a_o+bexp(－c－x)，(b＞0，C＜0)　　(3.17)

(4)风险偏好一般。在图3-7中，曲线E对应S型函数，当x＜k时，U'(x)＞0，U″(x)＜0，是风险规避的，当x＞k时，U'(x)＞0，U″(x)＞0，是风险喜好的。