【摘要】：目前，广泛应用的一种平稳性检验是单位根检验。随着计量经济学的发展，单位根检验的方法有多种，其中，应用较为常用的是DF检验和AD检验。
(一)时间序列的平稳性检验分析
在实际经济运行中，大多数情况下时间序列数据是具有一定时间趋势的非平稳序列。因此，在模型分析前，对于一个时间序列，有必要检验该序列是否平稳，即对时间序列数据进行平稳性检验。目前，广泛应用的一种平稳性检验是单位根检验。随着计量经济学的发展，单位根检验的方法有多种，其中，应用较为常用的是DF检验和AD检验。本文采用ADF检验方法进行平稳性检验，其检验原理为:假定时间序列是一个d阶自回归过程，增加因变量的滞后差分项来控制误差项的高阶序列相关。考虑到3种不同的虚拟假设:不含截距项、含截距项但不含趋势项、含截距项和趋势项，相应的3种检验回归模型分别为:
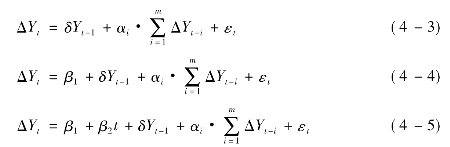
其中t为时间或趋势变量，εt为纯粹白噪音误差项，而ΔYt-1=(Yt-1-Yt-2)，ΔYt-2=(Yt-2-Yt-3)等所包含的滞后差分项的数目通常由实证研究决定，包含足够多的滞后项的思想就是使回归模型中的误差项序列不相关。在每种情形中，虚拟假设都是δ= 0，即时间序列是非平稳的，对立假设是δ＜0，即时间序列是平稳的。将每种情况下得到的Yt-1的估计系数除以其标准误来计算τ统计量，若计算出来的τ统计量的绝对值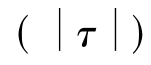 
超过了临界τ值，则拒绝δ= 0的虚拟假设，此时时间序列是平稳的;若计算的
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
