某企业的设备台数是什么变量

第四章　单位的选择

一

在本章和后面三章,我们将试图把某些疑难问题弄明白,这些疑难问题与我们所要研究的问题并没有特别的联系。所以,这几章有脱离主题的嫌疑,会暂时中断我们对主题的研究。我之所以提出这些疑难问题来讨论,是因为别人的处理方法对我所要研究的问题并不适用。

有三个疑难问题严重地阻碍了本书的写作进程,在我没有设法解决之前,我始终没有办法把自己的意见流畅地表达出来。这三个疑难问题是:第一,选择计量单位,该单位能适用于研究整个经济体制的许多问题;第二,如何确定预期在经济分析中的地位;第三,如何确定收入的定义。

二

经济学家们通常所用的单位不能令人满意的地方,可以从国民收益、实际资本存量和一般价格水平这几个概念中得到说明:

(1)国民收益(National Dividend),正如马歇尔和庇古教授所定义^[1]的那样,衡量的是当期产出或者实际收入,而不是当期产出的价值或者货币收入。^[2]而且,国民收益是个净概念,必须从当期产出中减去期初时已有的资本设备在当期的损耗,二者之差才是国民收益,才是社会资源的净增量,可以用来消费或留作资本。经济学家想在这个基础上建立起一个量的科学。不过假使这个定义以此为目的,则有一个严重不足之处:由于社会的商品和劳务是性质不同的复合体,因此严格地说,除了某些特殊情况,这个复合体是不能被计量的。例如,特殊情况之一是,所有产品都以同一比例增加。

(2)当我们为了计算净产出而设法计量资本设备的净增量时,遇到的困难更大。因为,要对现期内生产的新设备与已经损耗掉的老设备在数量上进行比较,我们就必须找出两者之间某个共同的基础。在计算净国民收益方面,庇古教授^[3]尝试减去“可以视为正常的折旧(Obsolescense)等,至于什么算是正常,则要看这些损耗是不是经常发生,使人可以大致(如果不能详细)预料得到”。但是,由于庇古教授并没有以货币作为计量单位,所减去的也不是一笔钱,因此他其实是假定:物质虽然没有变,但物质的数量已经改变,换句话说,他还是暗中引入了价值改变(Changes in Value)的概念,当生产技术改变,新的资本设备与旧的设备不相同时,庇古教授也想不出令人满意的办法^[4]来比较新旧两种设备的价值。

无论如何,就经济分析来说,我相信庇古教授所尝试的概念是正确而恰当的。但是,除非先采用令人满意的单位体系,否则,很难给出精确的定义。要把一个实际产出(Real Output)与另一个实际产出相比较,然后再用新的资本设备项目来抵消旧的、消耗了的项目,以计算净产出,这实在是个难题,而且这个难题真的没有什么办法解决。

(3)众所周知,一般价格水平这一概念含义空泛,而且也无法使其精准。这使得它很不适合因果分析(Causal Analysis),毕竟因果分析应该是非常精确的。

不过,这些困难也只不过是纯理论上的困难而已,工商界在做具体业务的决策时,从来没有顾虑过这类问题,而且与经济事态(Economic Events)的因果程序(Causal Sequence)也没有什么联系。这些概念虽然不明确,经济事态的因果关系却是明确的。由此我们可以断言,这些概念不仅不明确,而且没必要。显然,在我们的定量分析(Quantitative Analysis)表达方式中,一定不能使用任何在数量上模糊不清的概念。而且事实上正如我希望能证明的那样,一旦我们尝试进行分析,没有那些模糊的概念,事情反而会变得更加清晰。

两堆在数量上无法比较的东西,当然不能作为计量分析的材料,但我们仍然可以做以下粗略的统计比较。统计比较不需要精确的计算,只要大致不差即可。因此,在某些范围内,统计比较(Statistical Comparisons)倒是有意义的、健全的。实际净产出、一般价格水平等,最好放在历史的、统计的叙述里面,其目的在于满足历史的、社会的好奇心。对于这个目的,绝对精确既不是普遍的,也不是必需的;但是,因果分析则需要绝对精确,不论我们对于有关数量的实际值知道得是否完全准确。说今天的净产出大于10年前或1年前,但物价水平则较低。这句话与另一句话的性质很类似:维多利亚女王作为女王要比伊丽莎白女王好,但作为女人却不见得比她快乐。这句话不是没有意义,也不是没有情趣,但不适于做计量分析的材料。如果我们用如此空泛的、非量化(Non-quantitative)的概念来做数量分析的基础,那么我们的精确一定是戴着假面具的。

三

我们要记住,在任何特定场合,企业家最关心的是决定以什么样的规模来使用一定量的资本设备。当我们说,假使企业家需求将增大(总需求函数提高),则总产量将增大,实际是说,厂商将在同一数量的资本上雇用更多的劳动力。如果是一家厂商生产一种商品,则产量的增减有实际意义。但是,如果要把各厂的生产活动加总起来,则除非用给定设备上的就业量为标准,否则我们无从准确地说产量到底是增是减。在这里用不着社会总产量以及一般物价水平这两个概念,因为我们不需要当前总产量的绝对值,来比较当前产量与不同资本设备、不同就业量所能产出的产量之间的大小。如果为叙述方便或进行简单比较,我们要用产量增减这种说法,那么,我们必须依赖下列假定:在一给定资本设备上所使用劳动力的人数,确实是由此所生产产量的恰当指数,换句话说,我们假定二者同时增减,虽然二者并没有直接的一定比例。

在论述就业理论时,我建议只使用两个基本数量单位,即币值量(Quantities of Money-value)和就业量。其中,前者是严格同质(Strictly Homogeneous)的,后者可以人为地使其做到同质。因为对于不同等级和类别的劳动者以及领取薪金的办事员来说,他们获得的是相对稳定的报酬。为了便于计算就业量,我们可以把普通劳动者工作一小时的报酬作为计量单位,而按一定比例把特殊劳动者的工资报酬换算成他的劳动时间。例如,报酬是普通劳动者两倍的特殊劳动者每工作一小时,计作两个工作时数。我们的目的是通过这种方式得到理由比较充分的就业量的定义。我们把衡量就业量的单位叫做劳动力单位(Labour-unit),并把每一劳动力单位的货币工资称为工资单位(Wage-unit)。^[5]从而假设,E为工资或薪金总额,W为工资单位,而N为就业量,就有E=N·W。

单个工人在特殊技能以及对不同职位的适应性方面固然存在巨大差异,但这个不争的事实不足以推翻劳动供给具有同质性这一假设。这是因为,如果工人所得报酬与其效率成比例,则因我们计算劳动供给时也根据其报酬给予加权,所以这种效率的差别也已经计算在内了。假如,当产量增加时,一个厂商不得不雇用更多的工人,而这些工人的工作效率相对于付给他们的单位工资越来越低。如果是这种情况,也不过是许多因素之一使得某给定资本设备上所雇用的劳动力逐渐增加时,设备的边际产量逐渐递减的诸多原因之一。换言之,我们可以把报酬相等、效率不等这种劳动的不同质性,包括在资本设备里,看做是资本设备的性能。所以,当产量增加时,我们不认为是劳动越来越不适于利用同样的设备,而认为是设备越来越不适于雇用劳动。假如没有多余的专业技术工人,必须雇用技术差一点的工人,致使产品的平均劳动成本提高,这种情况表明,当就业量增加时,该资本设备的报酬递减速度,相比有劳动者剩余时更大。^[6]假如各类工种的专业化程度很高,工种之间根本不可能替代,即使在这种极端情况下,也没有什么不便讨论的。因为这无非表示,当专门适应某种资本设备的劳动力都已用尽时,则该种设备的产品供给弹性会下降到零。^[7]我们所作的劳动单位具有同质性的假设不会带来任何问题,除非不同劳动单位的相对报酬间出现极大的不稳定性。而即使真的出现了不稳定性,我们也可以通过作劳动力的供给和总供给函数的形状都会快速改变的假设来解决这个问题。

当我们把经济体制的运行当做一个整体来考察时,如果严格限定只使用两个单位,即货币和劳动,将避免很多不必要的麻烦。同时,把产量和设备的特定单位留待我们独立地分析单个厂商或单个行业的产出时使用,并把一些模糊不清的概念,例如,总产出量、总资本设备量和一般价格水平,用于某种历史比较的场合,而历史的比较在一定(也许还很宽广)的限度内本来就是不严密的和近似的。

据上所述,我们以后将借现有资本设备上所使用工时(Hours of Labour)的多少来衡量当前产量的变动,不管它是用于满足消费还是用于生产新设备;技术工人的工时则按照他们的所得报酬加权。我们不需要把这个产量与另外一组工人和设备所生产的产量做量的比较。在既定的资本设备条件下,当总需求函数变动时,企业家们将做出预测和反应;我们不必了解由此所生产的产量、生活水平和一般物价水平与另外一个时期或另外的国家之间比较会产生什么变化。

四

不论我们所讨论的是一个具体的厂商、一个行业,还是整个经济体系的活动,我们可以不问产量,只用总供给函数(Aggregate Supply Function)和我们所选定的两个单位来表示供给曲线(Supply Curve)和供给弹性(Elasticity of Supply)。例如一个厂商(对于一个既定行业或全部行业也基本是这样)的总供给函数式为:

Z_r=φ_r(N_r)

其中,Z_r是能使就业水平为N_r的预期收益(不包括使用者成本在内);预期收益达到Z_r时,足以引诱企业家雇用N_r人。假如就业量N_r能够引致产出O_r,设O_r=ψ_r(N_r),则可以推导出: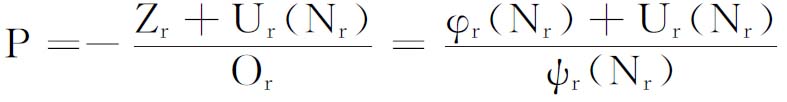

上式就是通常情况下的供给曲线。其中U_r(N_r)为就业量在N_r时企业家预期中的使用者成本。这样,在每一种商品都具有同质性的情况下,即对于每一种商品,O_r=ψ_r(N_r)都有确定的含义时,我们就可以用普通的方法来估计Z_r=φ_r(N_r);这种做法有一个好处是:我们不能用对N_r求和的方法来对O_r求和,因为,ΣO_r是不能用数值来表示的。而且,如果我们可以假设:在既定的环境下,既定的总就业量在不同行业间分配的方式是唯一的,以致N_r是N的函数,那么,问题可能会得到进一步简化。