政府债券合约期权的波动率矩阵结构

第五章　波动率估计的高级课题

上一章考察了波动率估计的标准方法，本章将涉及更多复杂问题和有关这一领域的边缘问题。

有关波动率估计的一般观点认为，布莱克和斯科尔斯模型精确地描述了实际期权市场的条件。主要假定在任何时间和市场水平下，通过有一个连续波动率σ的时间对数，促使标的资产价格变化。一个例子是，无论期权的敲定价格或到期日如何，用市场上的实际期权价格输入公式得出的隐含波动率都是一样的。因为存在这样一个事实，即同一到期日有不同的敲定价格和各不相同的到期时间导致隐含波动率不同，已经导致许多人对传统的布莱克和斯科尔斯方法的效果和基于类似假定的所有那些价格模型产生怀疑。

上一章隐含波动率部分我已证实了，因为期权的敲定价格不同，所以隐含波动率不同。尽管人们可以运用各种加权方法调整不同波动率之间的差异，得出一个综合波动率数值，但不幸的是，这一技术很明显利大于弊，因为它消除了有价值的信息才能得出结果，而这些信息运用隐含波动率模型（可将已知敲定价格和到期日输入模型）是能被理解的，而且不应忽视这些信息。现行智慧（不是简单地估计隐含波动率）要估计波动率模型，然后评价由这些模型导出的期权价格。

这一领域是如此重要，以至于它不仅仅需要整个一章讲述，而且研究它们可能会耗费期权理论家和市场投资者多年的心智。

首先，我们将考察如何运用敲定价格和时间组成隐含波动率模型。要做到这一点，我们将介绍波动率矩阵和从各种市场角度考察它们。

然后，我们将集中介绍有同一到期日的“笑容”隐含波动率模型。在这一部分，我们将介绍给读者的是不仅知道如何评估这一模型，而且懂得使它标准化，允许使用者即时指出错误价格机会。

我将通过察看资产种类不同和到期日不同的隐含波动率模型，继续分析和考察为什么存在这些模型。

所有这些将导致我们在期权定价方法上有一个潜在的突破。这是对期权定价高级模型的发展，这一模型综合运用了敲定价格和时间的隐含波动率模型。

最后，我将考察在一定时期内，如何利用波动率关系预测波动率。在这一部分，我将介绍远期波动率的概念，它可能正变成一个全新的和其他种类远期合约市场及利率和外汇市场一样大的市场。

波动率矩阵

要明白隐含波动率是如何随期权的敲定价格和时间的不同而变化的最好方法是，搜集所有有关数据，然后用表列出波动率。可以利用波动率矩阵做到这一点，这是一种被期权交易者和分析家使用的最重要工具之一。表5. 1介绍了这样一种波动率矩阵，它是金融时报100种股票指数期货（FTSE）期权和在金融时报100种股票指数期货市场期限为五年的到期日的店头交易市场（OTC）期权。

表5. 1　金融时报股票指数期货期权波动率矩阵

这一矩阵的数据由1994年8月9日的数据组成，并由伦敦BZW提供。^[1]表中不同的隐含波动率是由于标准敲定价格和到期日不同产生的。这一期权品种系列中，最靠近现行市场水平的敲定价格的隐含波动率是指期权处于平价或平价期权的波动率，这从矩阵的顶行中部可以看到。所以，增量为10%的期权敲定价格被认为会增长到30%以上，并处于现行标的金融时报100种股票指数期货市场价格水平以下。为了进一步帮助分析，波动率矩阵的结果经常被描绘成敲定价格和时间的模式。这已经在图5. 1中画出。读者可以看到，几乎所有的隐含波动率都是不同的。人们发现，同样的到期日，离平价期权水平越远，隐含波动率差异越大。

图5. 1　FTSE指数的期权波动率笑容

在图5. 1中，你能看到模型的形状是曲线向上，处于平价状态的期权所对应的隐含波动率相对较小。期权的敲定价格越高，平价期权的隐含波动率越低；期权的敲定价格高于现行市场价格30%以上时，波动率达到最低点。在许多市场上（我们将很快看到），这一曲线关系是对称的。那就是，期权的敲定价格离现行的标的价格越远，隐含波动率越高。描绘出的这种图形看起来如同一张笑脸。因而，对于同一到期日的期权被命名为波动率“笑容”（·○⌒·）。

传统期权波动率分析暗示：假如同一标的资产的期权的隐含波动率之间存在巨大差异，期权价格就会不正常，表明此时存在一个交易机会。在过去的日子，交易者针对这些反常现象浏览他的计算机，当隐含波动率低时买进所有“便宜”的期权，当隐含波动率较高时，卖出“熊市”期权。然而，无论他们这种交易已做了多久，始终存在不同隐含波动率的异常模式。为什么这些模式持续存在？这些模式中亏价期权（特别是相对于现行标的市场价格，敲定价格更低的期权）的隐含波动率高于平价期权的隐含波动率。一般地，对这一结果有三种解释：

（1）第一种解释是，处于较深的亏价期权存在通胀的隐含波动率。由于与平价期权相比，亏价期权存在不成比例的高开价和价差，例如，较深的亏价期权的理论价值为0. 02，本来应是0. 01的开价以0. 03开价，因此与它的公允价格相比，以0. 03的价格计价的隐含波动率评价将导致一个更高的隐含波动率。因为理论期权定价模型不能结合交易成本或开价/价差进行运算，因而从转换的期权定价模型看，这将扩大对隐含波动率结果的影响。

（2）第二种解释是，期权价格只部分由以期权定价方法为基础的理论假定确定，另一因素是由提供给投机者的亏价期权的供给和需求水平决定。另一方面，亏价期权变成盈价期权时，销售者将遭受损失，当他们只有少量期权时，为避免麻烦，将卖出期权。期权市场有一句格言：最小变动价位少于2个时，人们将永远不卖出期权。假如是这种情况，那么实际期权价格及其隐含波动率将相应高于公允价格和期权的“公允”波动率。

（3）第三种，也是最令人信服的解释是，市场不认为标的资产分布是一种对数分布。它有各种广泛的可能分布，具体如下：

●假如市场期望存在一个偏态分布（比如在金融时报100种股票指数期货波动率矩阵中看到的），

●或者市场根本不变动或经历急剧的价格变动（如爆炸）。

这种经常发生在真实市场中的情况被称做“细长峰谷”，这时候停留在看跌状态或变动超过两个标准差的市场概率更高。图5. 2描绘了这种情况和对数分布情况。

图5. 2　对数和细长峰谷分布

很清楚，由所有这些因子组成的隐含波动率模型偏离了预期的传统的期权定价模型的假定。与前面描述的一样，这些模型认定由于敲定价格和整个时间一致，所有的波动率处于同一水平。有趣的是，这些效果在不同市场是不一样的，每一种情况产生的隐含波动率模型都是惟一的。

在今天更复杂的市场中，不是隐含波动率最低时买入期权，隐含波动率最高时卖出期权，交易者会将隐含波动率与历史“笑容”关系进行比较，评估期权是“便宜”还是“贵的”。在这种思想指导下，我将告诉读者一种方法，评估不正常价格期权时，不与单个隐含波动率联系，而与有特定标的资产的隐含波动率“笑容”模式联系。

各种市场上的波动率“笑容”

金融时报100种股票指数期货“笑容”模式分析

仔细考察图5. 1的隐含波动率模式，可以很清楚地发现，金融时报100种股票指数期货期权的概率比很大变动的“对数”概率还要大，特别是往下移动时。这一结论也能推导出来，敲定价格低时的隐含波动率高于平价期权和敲定价格高时的隐含波动率。与突发性的巨大往上涨行情相比，市场对巨大的崩溃概率更敏感（存在偏见）。这种有趣的情形经常出现。过去，波动率模型形状相当“扁平”或至少是对称的。然而，1987年10月，由于股市大崩盘，发生了许多意想不到的事情。指数向下移动的事实已经证明，这比由历史数据支撑的往上涨造成的后果更严重。几乎世界范围内的指数期权的“笑容”里都是往下跌的曲线，这反映出卖方的担心（和投机者的贪婪），拥有亏价看跌期权受到的伤害（或获利）大于拥有亏价看涨期权。然而，了解1994年上半年金融时报100种股票指数期货戏剧性崩盘的任何人都知道，上述情况的出现并不意味着它提供了可以使用一种低的风险交易策略，即通过卖出亏价看跌期权（那是超值）和利用收益买入亏价看涨期权（那被认为低估的期权）来获利。

许多市场参与者会对期权价格的对数概率和隐含波动率概率之间的差异进行比较。要估计对数概率，人们必须输入平价期权的隐含波动率，并令一个计算机程序比如EXCELTM执行，得出所有的概率。按照现在所罗门兄弟（Solomon Brothers）的比尔·玛格耳伯（Bill Margrabe）说法，“假如对数曲线认为股票到期时价格在110以上的概率为1%，‘笑容’模式（概率）显示的概率就是10%，这就是一个强势的市场预期描述。”^[2]实际上，“笑容”模式现在包括在对标的资产价格的技术分析中，它认为在未来的某点，“笑容”模型可以得出一个一定价格条件下的更客观的概率估计。

金融时报100种股票指数期货“笑容”告诉我们，一个不同种类的概率分布只存在于期权交易者的头脑中，而不是对数概率分布中。离到期时间越远，期权市场的隐含波动率越高。假如因为担心最终崩溃发生，而令“笑容”模型是“偏态”的，离到期时间越长（最终有更多的潜在经济日），发生崩溃的概率越高。这也解释了隐含波动率增长情况。然而，离到期时间越远，“笑容”模型似乎越扁平。仅仅当我们开始接近期权的最后到期日时，“笑容”模型才由温和的撅嘴变为发狂的咧嘴，其他资产的模型也如此，下面将开始考察这种情况。

美元/马克的“笑容”模式分析

读者从表5. 2和图5. 3，可以看到波动率矩阵和相应的美元/马克期权图形。

表5. 2　美元—马克波动率矩阵

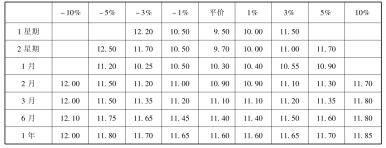
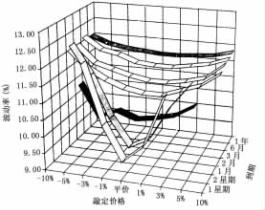
图5. 3　美元—马克期权的波动率笑容

这个矩阵的信息取自1994年8月9日的隐含波动率。^[3]这份数据期限仅仅是一年，但在此之后图形没有发生大的变化。在这个例子中，与敲定价格再高一点或更低一点的模型相比，目前敲定价格的“笑容”模型是更对称的。进而当期权离到期时间越远，隐含波动率也越往上升（如同发生在金融时报100种股票指数期货情况）。这些模式的含义是什么呢？

许多实证研究显示，外汇市场的变动既不是呈正态分布也不是呈对数分布。当概率根本没有发生变化时，外汇市场经常发生大的波动。部分原因是由于有中央银行周期性干预而使市场稳定。然而，无论什么时候中央银行平抑市场，靠的是中央银行不与汇率水平发生联系，银行突然而强烈地让市场回到银行认为合适的正常水平。当未这样做时，市场将维持在现行水平上，直至中央银行放弃不干预政策。当这种博弈结束，市场失去对中央银行维持秩序能力的信心时（中央银行对市场之争），汇率市场将崩溃。1992年9月英格兰银行发生这种事情，当时英镑以一个相当不体面的方式离开ERM。

但是概率的剧烈变动是上下波动，因为1992年9月英镑的崩溃也是马克的崩溃。在这个例子中，当干预生效时，货币将返回到健康的水平（从中央银行的观点看），如果干预失败，货币将走向其他方向。这就是为什么交易者调整亏价期权的价格以便反映到期日“笑容”的原因。但为什么我们采取行动时，隐含波动率上升更快呢？

美元/马克的波动率期限越长，就会越高于下几个月才到期的期权合约的隐含波动率。离到期日还有较长时间的期权的隐含波动率上升模式认为，波动率会回复到还有较长时间到期的期权的隐含波动率平均水平。另一种可能的解释是，市场期望迟早再发生一些重大经济事件并导致市场崩溃。假如这是一种合理解释，那么“怪物终将抓到我”的观点可能导致离到期时间还长时，有较高的波动率。

分析美元利率“笑容”模式

从表5. 3和图5. 4中，读者会发现一个波动率矩阵和美元利率的“期权图”。同样，表上数据取自1994年8月9日标的工具的隐含波动率。这些隐含波动率与一揽子利率期权的利率上限协议相联系。这些金融产品将在本书第十二章详细讨论，它将总结出，上限协议是利率的店头市场期权，金融机构提供这些产品给代理人，作为利率保险政策的组成部分。^[4]

表5. 3　美元利率期权的波动率矩阵

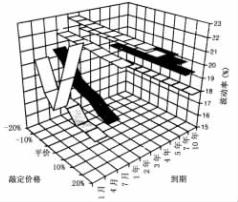
图5. 4　美元利率期权的波动率笑容

一般地，上限协议被限定在一年这样小的期限内，最长延长至10年。所以在这个例子中，短期内是不可能根据利率上限的隐含波动率来画出波动率“笑容”的。然而，人们能从交易所正在交易的同样外汇品种中推导出隐含波动率。我在后面第八章中将会讲到这些欧式美元期货期权产品。假如读者明白上限协议和欧式美元期货允许交易者从伦敦同业银行提供的美元利率变化中受益，上面这一点就好理解。两种产品的惟一差异是期权的到期日不同，同时欧洲美元交易可以利用任何一种工具，而上限协议是店头市场交易产品。所以，叙述中我已经包括下面这些期权，有1月、4月、7月到期的期权，另外为了可比，也包括上限协议波动率。^[5]

现在读者将发现，当对前面列出的金融时报100种股票指数期货期权或美元/马克期权进行比较时，存在各种不同“笑容”模式，如同期限结构模式一样。很明显地，离到期日只有较短时间的利率期权展示的模式完全不同于迄今为止已经研究过的市场上的模型。离到期日越远，波动率将在一年内一直上升然后开始下降。最后，从一年结束后到十年，“笑容”模式几乎不变。对于离到期时间更长的期权，根据一个扁平的波动率模式，认定利率的对数分布过程的假设是合理的。

本章后面将讨论为什么“笑容”曲线主要是指短期期权的情况。尽管在这些市场上很奇怪的是，离到期时间越长，隐含波动率反而下降。这是否意味着风险也同时下降呢？或许是，但大部分情况下不是。后面将给出一个更有说服力的解释，即主要是由于利率和波动率回归到一个长期均值。

政府债券合约期权的波动率矩阵结构

在所有的这些例子中，在某一特定时间点建立了波动率结构，以便对隐含波动率和“笑容”结构的相关水平进行比较。问题是这个矩阵仅仅能在当天使用，明天整个结构可能发生改变。例如，读者可以参考图5. 5，这是一个有关不同种类期权的三维图。由伦敦国际金融期货交易所研究部描绘的这一图形，说明了1993年12月政府债券合约期货的期权“笑容”结构。这也展示了从1993年10月20日至11月18日每天的“笑容”模式。从图上能看出“笑容”结构随时间变化的情况。如同前面描绘的金融时报100种股票指数期货的例子，“笑容”模式是“偏态”向下，但离11月18日期权到期日近时，图形似乎变得更对称和更似“笑容”模型。

不进行上面的描述，很难弄懂这类图形的意思。这是因为前面表格列出了敲定价格的固定范围，我从来不知道用哪一天来确定标的政府债券合约期权是处于平价。另外，隐含波动率整体水平是处于上升或下降，“笑容”模式比证实的图形变得更大或更小。最后，我最关心的是，图形告诉我这就是政府债券合约期权未来“笑容”模型。

表5. 1列示的金融时报100种股票指数期货波动率矩阵是由一个标准方法建立起来的，它利用过去的“笑容”信息确定未来的“笑容”模型。然而，估计“笑容”结构的目的是为期权定价和认定错误价格机会建立一个持续的和预期的方法。在这一部分，我将运用自己的方法，分步向读者介绍建立政府债券合约期货期权的波动率“笑容”估计程序。我选择这一市场是因为现在惟一有意义的数值是最近正在交易的期权，仅仅需要改变“笑容”关系的下一个96个日历日（约等于72个交易日）进行分析。然而，读者可以将这一方法运用到自己感兴趣的任何市场。

这一故事开始于我公司的一个意大利代理商需要在市场上进行政府债券合约期权交易时，需要咨询正面临的一个真正问题。主要的问题是他们不知道从何处着手估计波动率。在看了来自伦敦国际金融期货交易所（见图5. 5）的三维图画后，我觉得很有意思，但它仍不能满足交易者在期权定价时利用图上信息恰当评估未来隐含波动率“笑容”结构。面对这些问题，我要回到这些数据并重新开始计算。我要做的第一件事情就是画出“笑容”，而第一个要做的是利用上一章的表4. 7数字来画。因为一个“笑容”描绘的是与敲定价格有关的所有单个期权的隐含波动率，读者看到，“笑容”曲线是明朗的。图5. 6显示了1993年11月1日的“笑容”。这是发生在那一天的有趣的人工作品，我的目的是看利用这一信息预测“笑容”结构方法能否用在其他时间进行预测。这一模型能否用来预测，必须看其他时间的“笑容”模型是否与其相似。首先看图5. 5的伦敦国际金融期货交易所，我已经猜测他们是不同的。

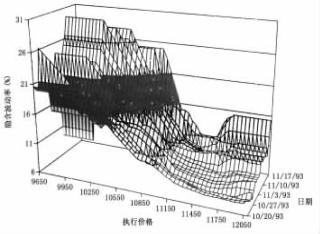
图5. 5　整个时期内BTP笑容模型的LIFFE图

图5. 6　1993年11月1日BTP期权波动率笑容

图5. 7　间隔两周的BTP笑容模型图

图5. 7显示，从1993年12月、1994年3月、1994年6月政府债券合约期货的有效期开始至终结，“笑容”结构三维图形不是每天而是每两个星期才相似。

问题变得很清楚：首先，“笑容”结构期权有效期内都在变化，越靠近终点变化越大。其次，因为波动率水平总是不断变化，不可以直接将隐含波动率水平和平价期权波动率水平进行比较。最后，因为标的政府债券合约期货价格期权有效期内不断变动，而且平价期权的敲定价格（“笑容”模型的底部）随标的政府债券合约价格变动，所以用同样固定的敲定价格画出的每一个“笑容”模型都是不正确的。总之，在考察改进政府债券合约期货“笑容”对称模型时，采用上述方法我已不可能再达到更理想的效果（相比采用伦敦国际金融期货交易所图形）。我需要做的是进行一些标准化。

估计未来定价期权的隐含波动率水平需利用历史“笑容”模式，历史“笑容”模型的现行标的资产水平和敲定价格的波动率绝对水平两方面必须标准化。这能通过波动率“笑容”指数（VSI）取得。

构建指数的步骤如下：估计每一天的“笑容”结构，用由现行的标的资产价格得出的敲定价格构建的敲定价格指数取代实际的敲定价格。敲定价格与现行的标的价格比率靠近1时的期权被称为平价期权。这一技术能使“笑容”模型中的敲定价格标准化，所以能在现行市场价格上在同样相对距离时进行比较。

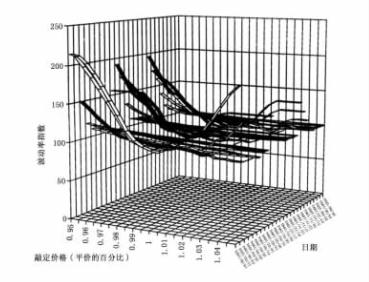
图5. 8　以平价敲定价格为标准的BTP笑容模型图

另一个问题是期权有效期内隐含波动率处于不同水平时，必须将其标准化以便从时间上对“笑容”结构进行比较。每一敲定价格的波动率除以平价期权的波动率后，乘以100得出结果。一旦完成这些步骤，期权有效期内进行“笑容”模型比较的主要困难已经克服。这可从图5. 8的三份政府债券合约期货到期的结果看到，甚至只有当期权已经标准化后，读者才能看到它们期权有效期内的变化。再则，分析似乎是困难的。但我看到：在整个期间内具有同一标的期权的波动率是不同的，因为期权到期日不同，它的“笑容”结构也不同。

假如我不仅仅比较期权有效期内同一标的政府债券合约期货的“笑容”结构，而且比较具有同一到期日而标的不同的政府债券合约的“笑容”结构，会得到一个连续模式。图5. 9展示了这一情况，读者可以看到，图形有些连贯性，因为三份标的合约的到期时间相对连续。

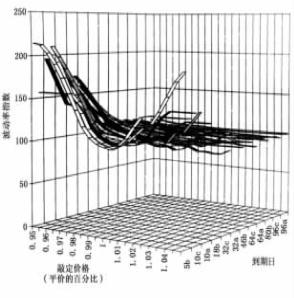
图5. 9　以敲定价格和时间为标准的BTP笑容模型图

在同一时间点进行比较时，波动率“笑容”模型相对稳定，现在可以得出波动率“笑容”模型的指数，它可通过对同一到期日的标准化“笑容”模型进行平均得到。然后，我利用这个一般的模型估计出输入的合适波动率，在期权定价中的任何相关的敲定价格和从离到期还有96日至终了日任何时间进行估计。图5. 10显示了期权有效期内的VSI指数。

所有分析家需要做的是，输入平价期权隐含波动率和到期日日历天数。利用过去同一时期的历史“笑容”关系的平均数代入公式，预期“笑容”结构自动产生。当交易的期权价格出现偏差时，分析家需要通过计算出的亏价期权波动率以便确定或评估期权的公允价格。他只要运用下列公式：

Vest= VSI/100×V平价期权

在这里：

Vest是交易者希望在定价中估计的敲定价格期权的波动率

VSI是期权到期日和相应的敲定水平的历史波动率“笑容”指数水平

V平价期权是被分析的有同一到期日的平价期权的现行隐含波动率

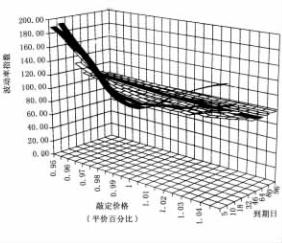
图5. 10　整个时期内BTP期权的VSI水平图

我将举出一个例子以便更清楚地说明上述问题。假如1994年7月22日，当政府债券合约九月期货的现行标的价格是113时，交易者希望确定一份标的价格为115.5的看涨期权的公允价格。要确定公允价格，必须估计这一亏价期权的波动率。

（1）第一步是应用上一章列出的技术，估计出处于平价且标的价格为113的看涨期权的波动率。

（2）然后将上面结果乘以VSI/100。

要找出波动率“笑容”指数（VSI）数值，我们必须考察当政府债券合约期权的到期日日历天数是32天和敲定价格对标的市场价格是115. 5/113或1. 02212时的情况。对于113，看涨和看跌期权的实际平价期权隐含波动率是10. 03%。^[6]我们现在需要找出的是离到期只有32天的一个相关的1. 02212敲定价格的波动率笑容指数数值。在表5. 4中你将发现，VSI因子表是相关敲定价格比率从0. 950到1. 050，从96日直至5日的各种到期日。

表5. 4　BTP期货期权的VSI矩阵

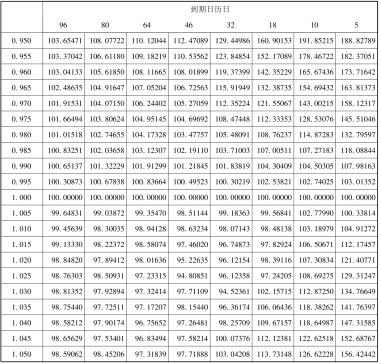
因为到期日是32天，我们查看“32”栏，直到发现VSI因子中敲定价格比率是1. 022123的那一栏。不幸的是，没有发现一个与这一值相关的敲定价格比率。然而，相关敲定价格比率应是在1. 02和1. 025之间。为了帮助读者寻找出波动率“笑容”指数因子，已经找出与之相近的1. 02和1. 025的敲定价格。因为我们要找的比率处于这两个数值之间，一个简单的线性外推方法可以用来得出准确的波动率“笑容”指数因子。下面这个公式可以做到：

现在，已经确定32天到期的敲定价格为115. 5的合适的波动率笑容指数，我们用这一数值输入这个公式，得出期权估计价格的准确波动率。

估计波动率为9. 641%，我们运用一个普通的布莱克和斯科尔斯定价模型〔实际上在这个例子中，布莱克（1976）〕得出期权的“公允”价格是0. 42或42个最小变动价位。

当然，运用这一技术会遇到一些麻烦，为了得出一个单一的敲定价格（不用说任何一个有广泛范围的敲定价格），需要进行许多计算来估计波动率。但这问题是很容易通过将上面的公式和波动率笑容指数表输入计算机程序解决，计算机将自动算出日历日和相关敲定价格比率。这就是我们最终要为意大利代理商做的事。就我所知，他们也是在市场上利用这个十分有用的工具的惟一参与者。我们知道，银行已经很好地将其用于“造市”和“套期”上。

“笑容”存在的含义

前面已经提到，知道敲定价格的隐含波动率“笑容”模式存在，表明标的资产价格对数分布过程中有些是相当错误的。已经说过，资产价格的对数分布产生不正确结果的程度是指在整个时间曲线不连续。例如，96天到期的政府债券合约期权的“笑容”模式几乎是扁平的，这表明对数分布与那一点市场预期的价格分布一致。然而，当期权靠近终点时，“笑容”首先出现在左边，离到期日越近，“笑容”越是向上卷曲。这表明离到期日越短，对数分布描述的政府债券合约价格分布对市场的解释力越小。

好像市场参与者在他们的潜意识中存在一个不同于实际对数分布的分布。这可以利用“笑容”结构推导出来。图5. 11列示了由不同到期日的隐含分布相对于对数分布的图形。人们将立即注意到96天到期的隐含分布几乎和对数分布一样。然而，离到期日越近时，从对数标准看，隐含分布变化越大。实际上，到期日差异是最大的，它类似于细长分布。

图5. 11　整个时期内BTP期权的隐含分布

假如期权有效期内到期日相同的隐含分布差异模式确实是一致的，人们将能把这一信息输入一个更好的定价模型。当我在本章后面描述最近发明的一种“超”期权定价模型时，将作详细描述。

读者是否认识到，到目前为止，我们仅仅一直集中分析一个单一时点的隐含波动率结构的扭曲图形。真实情况是，他已经检查了期权有效期内“笑容”如何变化，我们没有检查期权到期时隐含波动率如何变化的更详细资料。我将在本章下面讨论这一主题，考察期权有效期内隐含波动率是如何分布的。这就是波动率期限结构。

波动率期限结构

首先，我将定义什么是波动率期限结构。当人们使用布莱克和斯科尔斯定价模型（或类似东西）确定不同到期日的平价期权的隐含波动率时，将描绘不同到期日所对应的隐含波动率变化规律，并将这些点联结成一条曲线，即定义了整个分析期内的波动率结构，这就是波动率期限结构。让我们看几个例子。

本章前面介绍的波动率矩阵包括金融时报100种股票指数期货、美元/马克和美元利率矩阵，我们找到所有到期日的平价期权的隐含波动率。当描绘到期日期权时，可以评价期限结构。图5. 12a、5. 12b、5. 12c列出了这些标的资产期权的波动率期限结构。

图5. 12a　FTSE期权的波动率期限结构

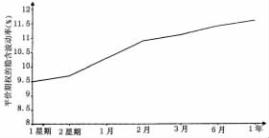
图5. 12b　美元—马克期权波动率期限结构

图5. 12c　美元利率期权的波动率期限结构

读者注意到，金融时报100种股票指数期货和美元/马克的期限结构曲线都是随时间推移斜向上，而美元利率波动率期限结构曲线是开始时向上然后斜向下。这些模型是如何产生的和为什么不同资产有不同的模型呢？要回答这些问题，让我们回到定价模型下得出的隐含波动率的假定。第一个假定是波动率是已知的常数和不变的，也就是它在整个时间内不发生变化。

我在上二章取得的证据已经驳斥了上述假定。第二个假定，波动率在整个时期内是同一的。上一章证据证实这一假定也是不真实的，有关经济日图形可看图4. 10。最后，到期日的标的资产价格直接与到期时间的平方根成比例这一假定也是不确切的。这一假定的意思是只要子弹射出枪膛就会击中谷仓门，即使射击点离谷仓门有几百公里远。

当有效期内波动率不是处在同一水平时，这些假定意味着期权定价模型存在错误（或至少术语是错误的）。图5. 12a、5. 12b、5. 12c展示了不是假定中所说的这种情况。这意味着期权定价模型假定中存在一些问题。为什么有效期内期限结构图形不是扁平的呢？有三种解释：

——价格过程的非平稳说

——波动率非均匀说

——波动率均值回归说

价格过程的非平稳说

非平稳是什么意思？这就是说，有效期内经济基本面变化会引起标的资产的价格预期分布的永久改变。假如分析家预期未来某一时期标的资产会发生重大变化，那么经济事件发生前和发生后的期权的隐含波动率将会不一样。

引起波动率增加的经济事件是改变了先前稳定的价格关系的经济事件。例如，意大利里拉对其他欧洲货币的波动率，过去是相当低的。在里拉下跌到ERM机制时，货币波动率随着其他货币变化而剧烈变动。假如意大利中央银行打算在ERM提取货币之前几个月在市场上披露信息，那么里拉对其他欧洲货币的波动率在这一日之前会走低，然后再走高。这一情况将导致一个向上的波动率期限结构，看起来如同图5. 13。

当然，期权到期时波动率减少会发生相反的情形。俄罗斯卢布波动率较高，假如俄罗斯政府宣布在三个月内卢布将与美元挂钩，波动率将会急剧下跌。然而，我们知道，卢布对马克的波动率将下跌到美元波动率水平，但在达到固定点之前将保持现行的高水平。这将是一个波动率向下倾斜的期限结构，下跌三个月后达到一个固定点，在那一点后的期权波动率将一直保持在这一水平直至终点。这一结果可以从图5. 14中看出。

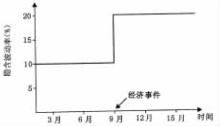
图5. 13　第1种波动率期限结构的非静态效果

图5. 14　第2种波动率期限结构的非静态效果

两个图形表明，随着经济事件的发生，隐含波动率预期会向上或向下波动。在经济事件日前后，波动率是一个常数。我有过多年的期权操作经历，从来没有发现过这样一种奇怪形状的波动率期限结构。所以，我怀疑这种“一次清”的非平稳说法能否解释非平滑波动率期限结构。主要理由是，政府或公司现有的有特定时间表（有计划）的政策改变是很少发生的。进而，他们要使这些政策不变化是很少的。当发生一些未知事件时，市场就会发生一些超出预期的情况。因而，市场参与者认定波动率期限结构会有向上或向下的斜率，假如他们相信在未来一些不知点上标的市场会发生一些基本的变化。

波动率非均匀说

波动率非均匀说认为，实际波动率在不同日子预期不一样，因为在特定某日会发生或不发生经济事件。上一章中，我们定义波动率高于正常波动率的日子为经济日。因此，未来波动率应当是期权有效期内实际发生的经济事件数量及其重要程度的函数。在期权有效期内，经济日出现的数量越多，相应的隐含波动率就越大。非均匀说的证据是什么？

上一章介绍的经验结果说明，当发生主要经济事件时，预期波动率是不同的，这些日子实际波动率更高，而非经济日的波动率是低的，甚至是0。这种非均匀将产生一个波动率期限结构。非均匀说假定经济日和日历日之间波动率存在差异。经济日包括当发生大事和影响标的资产价格的那些日子。日历日是直到一个特定期权的到期日的日子数值。非均匀说的证据是相当强的。除了上一章介绍的经济日子的影响，已知的两种市场现象例子也支持这一假设。第一是周末效应，第二是经济统计效果。

周末效应存在于许多市场，这是一种奇怪的结果，周末平价看涨期权的隐含波动率高于一周内其他交易日的隐含波动率。为什么星期一的隐含波动率高于星期五的呢？不能简单地说，全世界的人都憎恨星期一。对这一结果的可能解释是，大部分期权定价模型使用者在确定隐含波动率时，使用日历日作为时间输入模型。周末过程代表日历时间的损失而不是经济日。所以，期权的经济价值在整个周末是不变的。另一方面，期权定价模型没有区别日历日和经济日，由于损失两个日历日，期权定价模型将预测期权价格下降。假如从星期五到星期一期权价格保持不变，因为没有发生什么变化，期权定价模型计算出的隐含波动率中考虑了相对应的日历时间的一段负的影响。所以，这一效果支持前面章节介绍过的发现：当市场考虑经济日时，流行的布莱克和斯科尔斯定价模型是不能起作用的。经济时间不是日历时间，这在波动率市场是一个关键因素。

经济统计效果是一个奇怪的结果，重要的经济数据披露以后，交易期权的隐含波动率倾向于下降而不是上升。由于标的资产价格变动而导致实际波动率有时将急剧上升，同时隐含波动率下降。这又如何解释呢？最可能的解释是，披露经济数据表示当日是经济日而不是日历时间。然而，在市场不确定情况下先期释放的信息，使得过去的经济日造成巨大的经济损失。换一种方式说，按照时间衰减规律，经济日发生的损失比非经济日更大。然而，最可利用的期权定价模型不知道发生的一个特别重要的经济日已经过去，而将其认定为仅仅是另一个日历日。由经济日的过程引起的有效时间衰减效果是如此之大，以至于定价模型计算出的相对应的损失超过由于期权定价的隐含波动率减少导致期权价格的预期损失。

假如市场是有效的并能预测经济日的影响，那么隐含波动率将反映出来。随着经济时间的过去，隐含波动率下降幅度将大于日历时间预测的波动率下降幅度。这产生一个有趣而可能非直觉的结果，即披露重大经济数据的日子，实际即时波动率可以随着隐含波动率减少而增加。

最可能的是，由股票指数和外汇市场上看到的上升期限结构效果是由于标的资产价格系列的非平稳影响。

波动率均值回归说

这一解释如同字面意思一样：在一个给定的市场，波动率不能保持在极端水平，而是回到一个长期平均波动率，也就是从长期看，实际波动率将保持在一个稳定的水平。当波动率水平超过长期平均水平时，波动率会回到正常水平，而不是持续或扩展这种平均水平差异。其他经济日系列的许多例子也会表明，波动率最终会回到长期平均价值水平，包括政府管理的利率水平和中央银行干预货币市场。所以，认定资产价格的统计分布将在未来无限扩大这一假定是不合理的。在波动率期限结构上，这有什么效果呢？它引起波动率期限结构随时间向下倾斜。当读者回到本章开始介绍的波动率矩阵时，你将注意到美元利率的平价期权的隐含波动率是随时间变化而变得更低。要回答产生这一情况的可能原因，我们必须回到短枪和谷仓门例子。

就如我建议的一样，当我们掏出短枪时，如果我们所在位置离目标太远，子弹将不会射得太远以至不能够击中谷仓门。同样的，当期权有效时间还很长时，资产价格的效果变量不能无限增加，然而标准期权定价模型不能反映这一点。所以，当实际期权价格超出预期时，预期日历时间输入模型，模型仅仅能导出隐含波动率在下降。因此，隐含波动率不得不减少以便抵消随到期而增加的效果。隐含波动率的下降是人工推导均值回归效果的一种方便方式，它不需要输入像布莱克和斯科尔斯定价模型才能得出。

要改变现行定价模型中存在的问题，可以有两种选择：

（1）一种是继续使用标准期权定价模型，但输入期权到期日（或不同的敲定价格）的不同波动率。

（2）还有一种是选择另一种期权定价模型，它结合均值回归过程进行。假如已这样做，那么需要用一个常数波动率输入模型而无论期权的到期日是否相同。

解决这种均值回归假定有四个流行的定价模型。这些模型已经运用于利率市场，因为美元利率期限结构显示它们的波动率是最可能回归到长期期限平均数的。四个模型是霍（Ho）和李·莫德尔（Lee Model），^[7]布莱克、德曼（Derman）和托尼·莫德尔（ToyM odel），^[8]Hull和怀特·莫德尔（WhiteM odel），^[9]赫思（Heath），贾耳（Jarrow）和莫顿·莫德尔（Morton Model）。^[10]在第十二章讨论利率期权时，将详细讨论这些模型。

对所有这些模型作出调整的“目的”在于得出同一结果。当发生均值回归时，必须调整驱动市场的随机过程。资产价格变动的基本Wiener过程模型是：

作出调整的是均值（或趋动）期限μ，或波动率期限σ。前三个模型调整均值期限，最后一个模型调整波动率期限。这些调整使得最终资产价格统计分布（在这些例子中是利率）更分散和不再简单地与到期时间成比例。

这就好像人们扣动扳机时，由于重力效果的影响而使子弹朝下，使得子弹不能击中谷仓门。解决这一问题的方法是什么呢？使每一射击点高到足够抵消重力的影响（调整分布过程的均值）；或者得到一支更长筒枪，使得子弹更不分散和更集中于目标（通过调整波动率）。但读者可能得出这样的结论，这些模型仅仅用来处理均值回归问题，均值回归不是波动率期限结构不扁平的惟一原因。所以，模型目的在于修正所有引起期限结构更倾斜而不是扁平的因子。

修正“笑容”模型和波动率期限结构

首先这一部分要分析的是：期权定价模型中波动率为常数这一假定常常无效，分析家能为修正这一假定做些什么呢？答案依靠分析家正试图评价的期权。对于离到期只有很短时间的标准期权，输入现行平价隐含波动率的波动率“笑容”指数方法将改进期权定价模型的偏差。然而，修改的波动率常用在一个规则期权定价模型中，以便得出标准期权价格。

离到期日还有很长时间的期权不可能得出它的波动率笑容指数值，也就是说，对于一个店头市场（店头市场习惯的产品），在那里很难获得用于比较的基准隐含波动率。只有回到我们的老朋友即历史波动率那里，以相当灵活的方式运用上一章讨论的技术，才能找到答案。

幸运的是，我能与天才的金融经济学家——盖伦·巴格特（Galen Burghard），现在芝加哥的迪安·威特（Dean Witter）一起工作，他提出一个方法来得出非标准期权的历史波动率，这就是广为人知的波动率“锥”技术。

波动率“锥”

这一方法的基础是，假定期权的隐含波动率必须反映涉及期权的整个生命周期的实际隐含波动率的特定预期。假如是这种情况，当评估已经输入一个期权定价模型的波动率时，可以相当肯定地说，这个输入得出的波动率将不可能超过发生在过去可比时期内的最高实际波动率，或低于已经发生的最低实际波动率。所有分析家需要做的是，发现发生在过去的实际波动率范围。程序如下：

（1）分析家选择各种样本时间区域（例如一个月，三个月，一年等），然后估计持续时期内的历史波动率。在这种方式中，每月结束时可以估计出一个月的历史波动率，这是一个系列的历史波动率。假如连续这样做三年，那么人们将得出一个可以进行比较的历史波动率样本。

（2）在估计出整个分析期内所有历史波动率的总样本后，可以估计出最大、最小和平均波动率。在这种方式中，分析家很容易确定样本期的长期平均波动率和已经发生的最高或最低的波动率。

理论上说，人们使用定价期权估计的波动率将在已发生的最低和最高实际波动率之间变动并趋向于平均水平。

表5. 5列示了一个为政府债券合约期货市场建立的波动率“锥”，估计期是1991年10月到1994年5月，样本期各是一个月、二个月、三个月、六个月和一年期。

表5. 5　BTP期货的波动率锥估计

续表

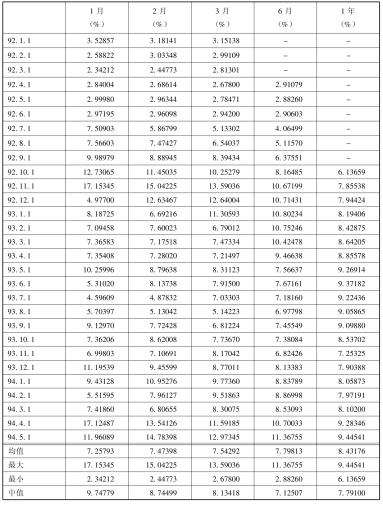
第一个实际波动率估计产生于1991年11月，当时合约已签一个月。在那一点，有足够的时间建立第一个月的波动率估计（基于这一结果的每日和每年收益），^[11]数值是3. 15117%。1991年12月，因为已经又过去一个月，可以再评估一个月的波动率。然而从1991年11月到12月结束，第二个月波动率是2.63920%。另外，头两个月（十月到十二月）估计的波动率是2.94384%。然后下一年的1月份，需要更新一个月和二个月的波动率，并增加第一个三个月历史波动率估计。这一过程中，每一新月产生时往前滚动，让我们去创造一个实际历史波动率的“移动”估计。

到1994年5月，为评估一些统计学数据，已经拥有所有样本期的波动率数值。表5. 5的最低一栏，读者会看到波动率的平均数、最大数、最小数和均值，它们分别是期间的平均历史波动率、最大波动率、最小波动率和在各自最大和最小波动率之间的中间波动率。当人们看平均波动率时，注意到样本期中，离到期时间越远，平均波动率越高。例如，当一个月平均波动率仅仅是7. 25793%时，一年平均历史波动率是8. 43176%。人们看均值波动率类似于统计学中的中位数。这一数值是最高和最低观察值的中间观察值，假如数据系列是正态分布，这一数值应当等于平均数。然而，在这个例子中，均值和平均值远远不相等。所以，波动率不是正态分布。有趣的是，这些均值波动率随时间推移而下降。所以，假如政府债券合约历史波动率的期限结构是向上或向下倾斜时，均值波动率是很难描述出来的。我猜测结果可能是向上倾斜。

当人们看最大波动率和最小波动率时，样本期加长时会发生一些奇怪的事。离到期时间越远，最大和最小波动率的分布越受影响。在整个时间段内，错误的历史波动率的最大盈余是最大波动率为17. 15345%和最小波动率为2. 34212%的一个月样本期。期限波动率“锥”是从他们的样本期中描绘的最大、平均和最小波动率中得来的。这能从图5. 15中看出，不难看出为什么这一图形被称做“锥”。

描绘在图5. 15中的波动率“锥”，因为需要比较，我已经将1994年4月到5月的政府债券合约期货中加上平价期权的隐含波动率。可以看到，平价期权的隐含波动率似乎保持在“锥”界限内，当它们开始靠近更上或更下边界时就又回归至长期期限平均数内。另外，更长期限历史波动率分布不如更短期限历史波动率分布的波动大，这一事实有力地证明，假如给定一个足够长的时间，波动率实际上还会回归至长期期限平均数。更短期限波动率一般地高于更长期限波动率，因为样本期不长时，无法取得一个足够大的样本观察值来得到一个稳定值。回到上一章Blackjack的例子：当我们仅仅交易8张扑克牌时，我们可能得到8张高的或低的牌。然而，当我们交易所有52张牌时，确信我们将交易16张“十”牌、4张“A”和32张低值的牌。样本期越短，由于“噪音”或经济日碰巧成堆发生或缺乏特定期，样本波动率将更可能发生波动。

图5. 15　BTP期货的波动率锥

波动率“锥”的存在不仅证实均值回归对期限结构起着重要作用，而且它也暗示，当我们评估过去较长时间的期权价格时，会发现波动率估计中的错误程度将是相当低的。既然在期权价格中波动率相当重要，这实际上可以看做是一个好消息。

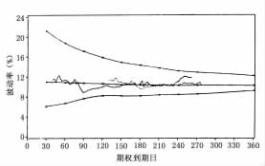
图5. 16a　美元—马克波动率锥

但是，这一波动率“锥”影响仅在政府债券合约市场发生吗？答案是否定的。感谢盖伦·巴格特和他的芝加哥迪安·威特团队，在这里再次画出图5. 16a、5. 16b、5. 16c、5. 16d和5. 16e。这些分别是美元/马克，美元20年国债期货、标准普尔500期货、牲畜期货和欧洲美元期货的波动率“锥”。几乎所有的这些“锥”建立时，都使用了上两年的数据分析历史波动率关系。例外的是标准普尔500期货，分析它时利用了过去四年的数据。这将再一次证实，对于所有这些市场，离到期时间越近，均值回归对于这些市场越重要。

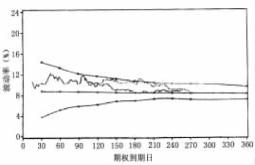
图5. 16b　美国20年国债期货波动率锥

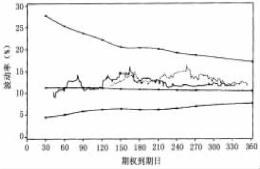
图5. 16c　标准普尔500期货波动率锥

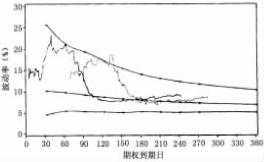
图5. 16d　牲畜期货的波动率锥

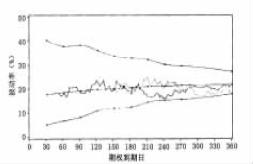
图5. 16e　欧洲美元期货波动率锥

在所有的这些波动率“锥”中，为了便于比较，平价期权的隐含波动率也被展示。可以看到，在整个时期内，“锯齿状”的系列在平均历史波动率上下之间波动。许多市场参与者通过将隐含波动率与历史波动率进行比较，增加了他们预测的波动率的准确性。假如历史波动率与隐含波动率之间差异很大，将会在不远的将来进行修正。这能从图5. 16d牲畜期货中得到证实。简单地说，隐含波动率超过了“锥”的向上边界面急剧往下。已经证实，这一分析工具给那些正在交易期权并渴望从中获利的人提供了在可以预计的未来隐含波动率将如何变化，因此一点不奇怪，这是他们成功的关键。

在此时总结我已经讨论过的期权价格的意义是再合适不过。市场参与者已经利用布莱克和斯科尔斯介绍的期权定价模型进行操作超过20年。由于原始模型中有某种麻烦的假定，后人对该方法作了许多调整，提出采用红利（1973年默顿）、各自的价格变动（二项式分布）、未来的资产价格不同于现行资产价格的概率（1976年布莱克）等方法进行调整。试图提出其他方法用于解决看跌期权（见第三章）和出现在整个时间的其他问题，即早期执行问题。然而，在大部分方法中，发展定价方法的基础仍是保持一些种类价格分布过程的假定即有效变量的对数与时间成比例。

对早期形式演进出的每一新的定价模型，不用怀疑已经有了改进，提出了一些重要的议题。但是坦率地说，这些改进的模式没有根本动摇原始布莱克和斯科尔斯模型中已有的东西。从这些新的定价模型获得的是一个迭代的改进，加进了一些新的思想，但同时也使我们更加迷惑。当然，这是一种学术探讨的方法，市场参与者包括我自己采纳了另一种方法：相比于最重要的因子——波动率，定价模型不再显得那么重要。在每天的期权交易中，这种观点已开始变成：或许真的存在一种“圣杯（Holy Grail）”，它同样为期权定价服务。

为“笑容”模型和期限结构建立的隐含波动率模型的整个过程，依赖于利用有缺陷的模型来得出波动率估计。然而，相应地，当分析家将这些隐含波动率输入有缺陷的期权定价模型，可以获得合适的价格。这类似于一个狗追赶它自己尾巴的例子，人们完全可以描述转圈的狗在追赶尾巴，但没有真正到达任何地方。尽管“笑容”模型和期限结构回归的偏见是连续的，然而它们也是可以利用有缺陷的模型调整波动率，以便反映假定中的错误并得出合理的价格。读者可能还记得我举的类似比喻的例子，布莱克和斯科尔斯期权定价模型的结果和“尼康”相机一样准确。我目前仍然坚信这一点。假如坚持假定，结果会产生一幅准确的世界图画。当运用的假定不准确时，价格也将会不准确。在相机例子中，拍出的画也会不准确时（也就是被歪曲），并不意味着人们就必须抛掉相机。只要稍微有点技巧，摄影者可通过调整相机主体部分的镜片或滤色镜，即修改胶片上的成像，以使影像更真实来修正相机。同样的方法也可以用在市场上，调整布莱克和斯科尔斯模型可以计算出更准确的“即时点”期权价格。

运用上述方法有许多优点：同样的基本定价模型能用在任何时间任何资产上。然而，针对每一市场，需要对模型进行不同的修改，以便取得准确的结果。这就如同每一标的市场都有它自己的镜片或滤色镜，必须将其附着于主体相机上，以便消除掉扭曲的东西。因此，需要分析每一标的市场波动率矩阵。但在某些点上，分析家必须要问自己，当有更好的和更合适的定价方法可以采用时，是否需要对基本期权定价方法作出调整。在相片世界，最终评定标准是已拍照片的质量。要提高图像质量，可以通过相机的镜片和焦距的反复调整来达到，并取得满意的效果。明显地，这是职业摄影家范围内的事情。另一种方法是利用相机可以自动调焦这一先进的技术进行调整。尽管这一技术相当复杂，但最终结果是一样的，即得到最逼真的照片。在期权市场，也在发生类似的事情。我们代替期权分析家在基本定价模型方面进行所有需要的调整，这时开发出一种新型的潜在的超模型，它使所有的调整自动进行。这是相当好的一件事情，因为自布莱克和斯科尔斯方法出现以来，这是期权定价方面的真正突破。

期权定价的超模型^[12]

1994年，来自大西洋两岸的三位研究者发表了研究报告，报告描述了期权定价超模型的发展，即自动地合并所有期权市场中的“笑容”和期限结构效果。伦敦帕里巴斯（Paribas）资本市场的布鲁诺·杜派尔（Bruno Dupire）和纽约的戈尔德·萨克斯（Gold Sachs）及伊曼纽尔·德耳曼（Emanuel Derman）和艾尔杰·凯尼（Iraj Kani）在《风险杂志》上发表有关他们发现的文章。^[13]1994年1月4日，马克·鲁宾斯坦（Mark Rubinstein）在波士顿美国金融协会进行了一个类似发现的演讲。演讲中提出超模型。

所有的方法都修改了基本期权定价方法，它通过修改特定市场的标的随机过程达到目的。为确定这一过程，他们要合并所有信息，这些信息从转换通常的布莱克和斯科尔斯方法来解决隐含波动率的“笑容”和期限结构所提供。基于此，他们建立一种模型，该模型在整个时期内与整个“笑容”模型一致（所以包括期限结构的影响），这是一个“完全”模型，因为此时利用理论和实际期权价格之差不能套利。

我们早就知道“笑容”模型和期限结构的效果，这一方法试图直接解决两个问题。已经试过的其他方法包括风险的非交易来源比如上涨、^[14]随机波动率^[15]或交易成本。然而，这些方法介绍的因子是不能套利的。运用的任何定价模型只不过仅仅是布莱克和斯科尔斯模型的改进。假如从定价模型得出的价格不同于实际交易市场价格，模型必须告诉我们如何组合一个同样的资产综合，允许我们锁定由模型产生的理论价格和市场价格之间的差异。超模型显然能做到这一点。在更正规的期限中，模型是随意的：期权价值不能依靠投资者对风险的评估而仅仅依靠套利方法得出结果。

在有效期内，超模型利用从标的资产价格和普通欧式期权市场价格获得的波动率函数取代布莱克和斯科尔斯模型中的常数的波动率期限。这些函数允许依赖敲定价格和期权到期时间。认定的随机过程公式如下：

当其他方法试图从理论上寻找波动率函数σ（S，t）时，超模型利用实际市场隐含波动率来解决这一问题。波动率函数以这样一种方式进入模型：当理论期权价格与市场价格一致时，仅仅包括输入的单个波动率。要更好地描述这一工作是如何进行的，我们将从布莱克和斯科尔斯模型的连续时间状态移动得出二项分布方法的离散状态。

读者可以回忆第三章，那里介绍了二项分布，标的资产价格以离散增量变动。当这些增量变得越来越小时，二项分布方法与布莱克和斯科尔斯方法的结果是一样的，而同时假定波动率为常数等。这一过程看起来如同那一章中画出的传统“树型”图，图5. 17再次描绘了这一过程。但德耳曼和凯尼指出，他们正在考察的标准普尔500市场的隐含波动率是不连续的，图形由一个“笑容”图形和波动率期限结构组成（对于1993年5月1日这一市场），这可从图5. 18中看出。很明显，敲定价格和到期日不同，波动率也不同。这与我在本章前面列出的所有波动率矩阵一致，而与标的标准普尔500的二项分布过程的假定不一致。

图5. 17　股票价格的标准二项式过程

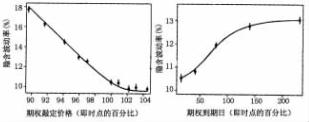
图5. 18　1993年5月5日标准普尔500笑容和期限结构图

现在有趣的事情出现了：他们修订“树型”图来考虑这些波动率结构，得出一个隐含“树型”图，这能从图5. 19中看出。他们说：“对于从已知期权价格中获得的所有敲定价格和到期日，将确定头寸和隐含树上达到每一节点的概率。”^[16]一旦已经画出“树型”图上估计的隐含波动率节点，那么就能画出所有时间点上的其他节点上的所有情况。根据离到期日最长的期权的最后到期日能够估计出通过由标准期权组合建立（那是在树型）的头寸，进而能够估计出标的资产或“熊市”证券无风险利率的头寸。

图5. 19　隐含于标准普尔500笑容的隐含随机过程

一旦知道整个隐含随机过程，那么隐含树不仅能评估普通欧式期权，而且也能正确地估价其他更广泛的相机抉择情况（非标准期权比如特定的店头市场和美式期权）。另外，本书后面第十三章讨论的变异期权也将利用隐含树定价。最后，所有相机抉择定价一致方法的存在，意味着所有期权或如同期权一样的债券能进行套利。这是因为作为风险管理的所有希腊衍生品现在与同一随机过程一致，并能直接进行比较。这回答了许多金融机构的一个关键问题：在一个连续操作方式中如何进行期权头寸套利。

显然，期权定价的演进加速解决了本章提出的许多问题。我们要求读者阅读前面关于完全暴露方法。与我们前面讲过的类似，据说这一研究已经促使为每一个市场建立自动相机系统。依靠所有标准期权定价模型的持续利用来确定隐含波动率过程是很重要的。当每一个人都利用超模型对期权定价时，隐含分布来自于对超模型的再校准吗？显然，超模型肯定是对原始的布莱克和斯科尔斯方法的升华。然而，它很可能促进而不是取代传统方法。在变异期权结构和欧式期权与美式期权定价的比较方面，超模型提供给分析家一个更好的方法，这也是超模型的主要优点。

在本章最后部分，我将讨论远期波动率的估计和它对期权定价的意义。

远期波动率的估计

毋庸置疑，不同到期日期权的隐含波动率不可能总是相同，正是这一事实导致市场上存在获利机会。

利率市场上，最需要强调的是处置利率期限结构。固定收益交易者和货币市场交易者总是看收益曲线与“误价”证券一致，因此开始设置利率套期策略。由于利率计算方法不一样，收益曲线种类是不一样的。估计收益曲线最简单的方法是利用收益曲线，将标的工具的到期日与这些收益相对应的到期日联系起来。另一种方法是确定“零息票”收益，它不与单一工具而是与一个特定时点相联系。这些“零息票”收益是指在他们的生命期内，它与没有付出息票或其他现金流出的工具相联系的收益，仅仅到期日付出本金。因此，为了纯粹的贴现价值而购买今天的证券，将为投资者提供一个确定的收益率而不受“息票”再投资问题的困扰。典型的息票工具常常指由政府发行的短期到期的贴现证券（常指Bills债券）。“零息票”工具常常指由扣除“息票”或从更传统工具，比如债券的本金支付方式综合建立，单个作为“零息票”卖出它们。在利率市场，从今天到未来某一确定点上，这种收益被作为评估利率收益最合适的方法。

在期权市场，波动率期限结构（从今天到未来各点的波动率）与“零息票”利率方法最相似。利率市场确定收益的另一种方法是评估远期或未来收益。涉足最近十年利率市场的人都知道远期利率的重要性。它们是一些证券，比如远期利率协议、金融期货和利率互换的基础，这些基于利率的衍生产品将在本书第十二章详细讨论。

随着远期起始期权的引进，远期波动率正在变得日益重要。这些“后付”期权和延迟期权将会在第十三章讨论。与利率的远期合约相比，远期利率的关键是确定未来波动率。要估计远期利率，需要引入“零息票”期限结构。期权的波动率期限结构能够估计出远期波动率。图5. 20列示了我们试图估计的远期波动率。

要发现什么是远期波动率，我们要做的是运用一个类似于远期利率协议（见第十二章）的公式。我们必须确定远期变量，σF2和开平方根。确定远期波动率的公式如下：

图5. 20　波动率期限结构确定隐含远期波动率

让我们看几个例子。假定我们对政府债券合约期货从6个月（181天）到一年（365天）的远期波动率有兴趣。6个月隐含政府债券合约波动率是7. 85%，一年隐含波动率是9. 35%，^[17]将这些数值输入上述公式得出：

10. 621%是指从隐含波动率的现行期限结构得出的隐含远期波动率。这一数值能运用到未来才开始的政府债券合约期权定价上，或用在波动率期限结构的即时“误价”机会上。

人们可以想像，因为波动率是指对标的资产价格变动风险的计量，离到期日越远，风险也越小。这一定理与市场上坚持的比如股票指数期货期权和政府债券合约期货期权的非均匀说假定一致。这一因子不仅解释了为什么波动率期限结构是向上倾斜，而且解释了波动率期限结构与远期波动率的增长是相联系的。市场价格从期限结构方面可能以无规则方式变动，它可以通过估计期限结构的远期波动率来察觉这一点。假如波动率是连续的，分析家可以将远期波动率与历史波动率“锥”进行比较。假如两者之间差异明显，分析家可以预期整个期限波动率会回到他们的长期平均数，远期波动率又回到线性状态，这可以通过后面第七章将要讨论的“日历”或时间差异来做到这一点。当在后面详细讨论这一点时，大家会很清楚，它们是如何运作的。

从我们上面的例子看出，六个月的估计波动率是10. 621%，从政府债券合约期货的历史“锥”看，政府债券合约期货的六个月平均波动率是7. 79813%（见表5. 5）。我们预计远期波动率水平将下跌至这一水平。将发生什么情况呢？仅仅从波动率期限结构形状的变化就可看出。当估计远期波动率时，上面公式将证明，远期波动率惟一的下降方式是，到期时间越长，波动率（一年）越下降，到期时间越短（六个月），波动率越上升。因此，人们可以运用的交易策略是，到期时间短且波动率上升时买入，到期时间长且波动率下降时卖出，预测这时期限结构更扁平或甚至是反转。一旦发生这种情况，会有一个预期获利，交易者将卖出到期时间短的期权和买入到期时间长的期权。

读者可以总结，基于远期波动率的相机抉择权利的存在为期权市场增加了一种新的方法。不仅期权交易者对波动率将来如何变化会有一个更清晰的看法，而且大量使用远期期权，造成波动率的期限结构变化，使期权组合暴露“套利”更有效。远期利率协议和远期外汇交易这一领域变得与期权市场一样重要，实际上我很少怀疑这一点。这些远期期权在市场“扩展”上是一个必备的工具，因为波动率是时间的函数，相应地让投资者更彻底地弄清这些证券。

这一章的结论是很清楚的，布莱克和斯科尔斯期权定价模型的一个假定，即期权的标的市场的分布过程是一个随机游走过程是错误的。市场参与者不再忽视波动率“笑容”和期限结构的存在，而且加以仔细研究。这已经导致对原始期权定价模型进行特别的修改，或期权定价方面发展了超模型。假如要在期权定价方面有理论上的重大突破，需要做的是对本章提出的议题进行更仔细地考察。

【注释】

[1]十分感谢伦敦的BZW的尼兰·迪·西尔维娅（Niran de Silva）和利·巴克森德（Leigh Baxendale）友情提供这一信息。

[2]引自1994年5月《期货杂志》文章，第30页，米兰玛·本瑟曼著（Miriam Bensman）：《挖掘期权点的价值》。

[3]十分感谢伦敦货币期权交易所的保罗·艾克德（Paul Akeroyd）友情提供美元/马克波动率矩阵数据。

[4]这一数据由美国内部资本经纪行提供，理查德·曼尼尔（Richard Mannell）协助。

[5]分析中不可能包括更多的欧洲期权到期日，因为1994年8月，撰写本章时，可利用的欧洲期权隐含波动率仅仅有1994年9月、1994年12月、1995年3月到期。

[6]这是由于看涨—看跌平价。

[7]霍和李：《期限结构变动和定价利率相机选择权利》，《金融杂志》，第41卷（1986年12月），第1011～1029页。

[8]布莱克，费雪，伊曼纽尔·德曼（Emanuel Derman）和威廉·托尼（William Toy），1990，《单因子利率模型和在国债期权中的运用》，《金融分析家杂志》（1990年1～2月），第33～39页。

[9]赫尔（Hull），约翰（John）和怀特：《定价衍生利率证券》，《金融研究评论》，第3卷，第4号（1990），第573～592页。

[10]赫思，戴维德，贾耳和莫德尔：1990，《债券定价和利率的期限结构：一种新的方法——相机选择权利评估》，《金融和数量分析杂志》，第25卷（1990年12月），第419～440页。

[11]为同样理由看第4章，由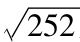乘以每日标准差。

[12]这一部分参考1994年《风险杂志》Graham Cooper的文章，标题是《超模型时代的到来》，我要感谢《风险杂志》的Peter Field，他让我得到这些资料。

[13]杜派尔·布鲁诺：《“笑容”的定价》，《风险杂志》，第7卷，第1号（1994年1月），第18～20页和伊曼纽尔·德耳曼和艾尔杰·凯尼：《“笑容”的摆脱》《风险杂志》，第7卷，第2号（1994年2月），第133～140页。

[14]罗伯特·默顿（Robert Merton）：《当标的股票收益是不连续时的期权定价》，《金融经济学杂志》，第3卷，1976年，第125～144页。

[15]鲍尔，约翰和怀特：《随机波动率资产的期权定价》，《金融杂志》，第42卷，1987年，第281～300页。

[16]德耳曼·伊曼纽尔和凯尼·艾尔杰：《摆脱“笑容”》，《风险杂志》，第7卷，第2号（1994年2月），第333页。

[17]读者可以回忆，政府债券合约期货期权在三个月到期时没有交易。然而，用更长的到期日获得政府债券合约店头交易期权是可能的。这里是关于如何得出这些隐含波动率。