第三章 财务估价基础
【学习要点】本章对理财中的财富增长及相应风险进行描述,需掌握下列要点:
(1)财务估价的范围及基本价值观念;
(2)风险的种类,投资报酬与风险的关系;
(3)资金时间价值及其计算;
(4)风险衡量的方法。
【主旨语】物有所值,随时空变化。 ——编者
第一节 财务估价概述
一、财务的基本价值观念
财务价值观念是财务管理的基础,观念的更新会带来管理水平的提高。一般而言,财务管理应具备的价值观念很多,如资金的时间价值观念、风险收益均衡观念、机会损益观念、边际收益(成本)观念、弹性观念、预期收益观念等。资金时间价值观念和风险收益均衡观念是财务管理最基本的价值观念。
(一)资金时间价值观念
资金时间价值就是一定量的货币在不同时点上具有不同的经济价值,其差异称为利息。资金时间价值可以用绝对数表示,也可以用相对数表示,它是资金所有权与资金使用权相分离后,资金使用者向资金所有者支付的一种报酬或代价,以利息额和利息率来表示。利息作为重要的经济杠杆,在宏观方面可以吸收社会闲散资金用于扩大再生产、促进资源合理配置,在微观方面可以刺激现代企业合理使用资金、加强资金周转、提高投资效益。因此,现代企业财务管理人员应充分认识资金时间价值,在财务管理活动中确立资金时间价值观念,重视利息的作用,并且按照经济上合理性和可能性的要求,进行最优方案的选择。
在实际的财务管理中,资金时间价值又往往与现金流量有关,同时还需把不同时期的现金流量按一定的折现率折算为同一时点的现金流量。所谓现金流量,是指在长期投资决策中,一个项目所引起的企业现金支出和现金收入增加的数量。按其发生的时间可分为初始现金流量、营业现金流量和终结现金流量等三类。
(二)风险收益均衡观念
风险是指在一定条件下和一定时期内可能发生的各种结果的变动程度,它与不确定性是有区别的。风险是现代企业在组织活动过程中不确定性因素的作用使实际财务收益与预期财务收益发生差异而带来的蒙受经济损失的机会和可能。市场经济的进一步发展,使企业在融资、投资、营运、分配等方面的风险日益加大。另外,企业内外部环境的变化也会给财务活动带来风险。因此,企业财务管理人员必须通过风险回避、风险转嫁、风险接受、风险分散等手段,对企业财务活动的风险加以控制,以正确、有效地实施财务决策。
风险与收益是一种对称关系,它要求等量风险带来等量收益,即风险收益均衡,这种均衡是市场竞争的结果。风险与收益均衡观念的核心就是要求企业不承担超过收益限度的风险,在一定的风险下收益必须达到较高的水平;在收益一定的情况下风险必须维持在较低的水平。
二、财务估价的应用范围
财务估价是指对一项资产价值的估计值。这里的资产可能是金融资产,也可能是实物资产,甚至可能是一个企业资产。这里的价值是指资产的内在价值,或者称为经济价值,是指用适当的折现率计算的资产预期未来现金流量的现值。财务估价也是对企业未来效率水平进行科学量化的过程,是对企业的持续经营价值进行判断、估计的过程。无论是对于投资者,还是对于企业管理人员,科学地进行财务估价,准确地了解企业价值,都具有重大意义。
(一)财务估价的意义
1.财务估价是企业理财决策的基础
企业的理财目标是企业价值最大化,为实现企业价值最大化,应科学地进行投资与融资决策。理财决策所应遵循的基本原则是,能够导致企业价值最大化的理财方案才是最优的决策方案。一般而言,在投资决策中拥有正的净现值的投资方案能导致企业价值最大化;在筹资决策中能使企业加权平均资本成本最低的筹资方案能导致企业价值最大化。
2.财务估价是企业确定资产经济价值的重要方法
财务意义上的资产的价值,是该项资产在未来企业持续经营中所带来的现金净流量所折合成相当于当前的总现值,即资产的经济价值。在财务估价中,一项资产的经济价值与该项资产过去的支出无关,资产的经济价值在于其能够在未来的使用中带来经济利益,所带来的未来经济利益表现为现金净流量。在理财决策中,依据财务估价所确认的资产的价值是否大于其市场价值就可以对该项资产的投资进行决策。如果资产的经济价值大于市场价值,则说明市场低估了该项资产的价值,投资于该项资产,可以获得净现值,方案是可行的;反之,如果资产的经济价值低于市场价值,则说明市场高估了该项资产的价值,投资于该项资产的净现值为负数,方案是不可行的。
(二)财务估价计量标准
对企业资产价值估价计量时,存在着多种标准,如历史成本、重置成本、可变现净值、现值、公允价值等。
1.历史成本
在历史成本计量下,资产按照购置时支付的现金或现金等价物的金额,或者按照购置时所付出的对价的公允价值计量。负债按照因承担现时义务而实际收到的款项或者资产的金额,或者承担现时义务的合同金额,或者日常活动中为偿还负债预期需要支付的现金或现金等价物的金额计量。
2.重置成本
在重置成本计量下,资产按照现在购买相同或相似资产所需支付的现金或现金等价物的金额计量。负债按照现在偿付该项债务所需支付的现金或现金等价物的金额计量。
3.可变现净值
在可变现净值计量下,资产按照其正常对外销售所能收到现金或现金等价物的金额扣减该资产至完工时估计将要发生的成本、估计的销售费用,以及相关税费后的金额计量。
4.现值
在现值计量下,资产按照预计从其持续使用和最终处置中所产生的未来净现金流入量的折现金额计量。负债按照预计期限内需要偿还的未来净现金流出量的折现金额计量。
5.公允价值
在公允价值计量下,资产和负债均按照在公平交易中熟悉情况的交易双方自愿进行资产或负债清偿的金额计量。
上述计量属性中,按依据的基础不同,可分为两类。第一类计量属性以所处环境下的市场状态为基础,会计人员以现行已知的金额——交易价格作为入账金额。这类计量属性包括历史成本(收入)、现行成本和现行市价。这类计量属性着眼于价格。第二类计量属性根据现存信息预测未来的现金流量,根据未来利益或牺牲来确定资产的现行经济价值。这类计量属性包括可变现净值和现值。这类计量属性着眼于经济价值。若按时间序列又可分为过去、现在和未来三种属性。历史成本是过去交易的代价,属于过去时态的计量属性;现行市价和现行成本是计量对象现在的现金等值,是现在时态的计量属性;可变现净值和现值是计量对象未来的流入(或流出)金额,因而它具有未来时态的计量属性。
第二节 资金时间价值
一、资金时间价值原理
企业财务估价是借助资金时间价值的计算形式来进行的。资金时间价值是指一定量资金在不同时点上的价值量的差额。资金时间价值来源于资金在运动过程中,经过一定时间的投资与再投资后所产生的增值。
在市场经济条件下,今天的1元钱和将来的1元钱是不等值的,前者要比后者的价值大。例如,将今天的1元钱存入银行,若银行存款年利率为10%,一年以后就会是1.10元。可见,经过一年时间,这1元钱发生了0.10元的增值,今天的1元钱和一年后的1.10元钱等值。这就是资金在投资后随时间的推移而产生的增值,也就是资金时间价值,它可以用绝对数来表示(本例中的0.10元),即利息。也可以用相对数来表示,增加价值与投资价值的比值(本例中的10%),即利息率。
资金在投入生产经营过程后,其数额随时间持续而不断增长,这是客观存在的经济现象。资金在投资过程中,不断按照投入—回收—再投入—再回收周而复始地运动,资金时间价值是资金在周转使用中产生的,是资金所有者让渡资金使用权而参与社会财富分配的一种形式。
通常情况下,资金时间价值相当于在没有风险和没有通货膨胀条件下的社会平均资金利润率,这是利润平均化规律作用的结果。在市场经济中,由于竞争,企业的财务管理活动总是存在着不同的风险,而通货膨胀是客观存在的经济现象。因此,同样多的资金在相同的时间投资不同的项目,所获得的投资报酬率是不同的,而它们之所以不同,是由于它们所产生的风险报酬率不同,时间价值(社会平均利润率)是相同的。企业在投资中,所赚得的基本报酬也必须达到社会平均利润率,否则还不如投资于其他项目或其他行业。只有购买国库券等政府债券几乎才没有风险,如果通货膨胀率为零,则可以用政府债券利率来表现资金时间价值。
银行存款利率、贷款利率、各种债券利率、股票的股利率都可以看成是资金投资的报酬率,它们与资金的时间价值率是有区别的,只有在没有风险和没有通货膨胀的条件下,时间价值才与上述各报酬率相等。值得注意的是,通常情况下,在讲述资金时间价值时,均假设只有在没有风险和没有通货膨胀的条件下,以利息率来代表资金的时间价值。
资金时间价值以商品经济的高度发展和借贷关系的普遍存在为前提条件或存在基础,它是一个客观存在的经济范畴,是财务管理中必须考虑的重要因素。在经济活动中,应将资金时间价值作为一种观念引入财务管理中,在有关的融资、投资和资本收益分配的财务决策中,都要认真考虑资金时间价值。
二、资金时间价值的计算
(一)一次性收付款项的终值与现值的计算
在某一特定时点上一次性支付(或收取),经过一段时间后再相应地一次性收取(或支付)的款项,即为一次性收付款项。例如,某人持有一笔现金10000元,现在按年利率为2%的5年定期存入银行,5年后取得本利11000元,这种收付款项就属于一次性收付款项。
资金时间价值的计算,主要是对终值和现值的计算。
终值又称将来值,是现在一定量资金折合成未来某一时点上的资金的价值,俗称本利和。
现值又称本金,是指未来某一时点上的一定量资金折合为现在资金的价值。上例中,10000元存入银行,5年后获得本利和11000元,因而现在的10000元经过5年后的终值为11000元;反之,5年后的11000元折合为现在的价值为10000元。现在的10000元与5年后的11000元在价值上是等量的。
终值与现值的计算涉及利息计算方式的选择。目前有两种利息计算方式,即单利和复利。单利方式下,每期都按初始本金计算利息,当期利息即使不取出也不计入下期本金,计算基数不变。复利方式下,以当期末本利和为计息基础计算下期利息,即利上加利。现代财务管理中一般用复利方式计算终值与现值。
1.单利的终值和现值
为计算方便,这里假定如下符号含义:I为利息;P为现值;F为终值;i为利率(折现率);n为计算利息的期数。
1)单利终值的计算
单利终值的计算公式为
F=P×(1+i×n)
【例3-1】 某人将现金10000元存入银行4年,银行年利率为2%,若按单利计息,则4年后所获资金为
F=10000×(1+2%×4)元=10800元
2)单利现值的计算
单利现值的计算公式为
P=F÷(1+i×n)
单利现值的计算同单利终值的计算是互逆的,由终值计算现值的过程称为折现。
2.复利的终值和现值
1)复利终值的计算
复利终值的计算公式为
F=P×(1+i)n
【例3-2】 某人将10000元存入银行,年利率为2%,则经过一年时间的本利和为
F=P+P×i=P×(1+i)
=10000×(1+2%)元=10200元
如果此人并不提走现金,将10200元继续存入银行,则第二年本利和为
F=P×(1+i)×(1+i)=P×(1+i)2
=10000×(1+2%)2元=10404元
同理,第三年的本利和为
F=P×(1+i)2×(1+i)=P×(1+i)3
=10000×(1+2%)3元=10612.08元
第n年的本利和为
F=P×(1+i)n
其中,(1+i)n通常称为“一次性收付款项终值系数”,简称“复利终值系数”,用符号(F/P,i,n)表示。如本例(F/P,2%,3)表示利率为2%、3年复利终值的系数。复利终值系数可以通过查“1元复利终值系数表”直接获得。
附录A复利终值系数表的第一行是利率i,第一列是计息期数n,相应的(1+i)n在其纵横相交处。由该表可查出,(F/P,2%,3)=1.061,即在利率为2%的情况下,现在的1元和3年后的1.061元在经济上是等效的,根据这个系数可以把现值换算成终值。
【知识链接】 复利是世界第八大奇迹
如果有个储蓄罐,只要你每天按照倍增方式往里面存放面值一分的硬帀,即第一天放进一枚、第二天放进两枚、第三天放进四枚,依此类推,坚持一个月,月底你就可以成为千万富翁。
换一个角度,仅以一元钱为本金,如果一定周期内能复利性质地增长一倍,那么只需三十个这样的周期,就可获得五亿三千六百八十七万多元。这就是复利的威力,也是财富增长的奥秘。对此,爱因斯坦有经典的评述:“复利的计算是人类世界的第八大奇迹”。
2)复利现值的计算
复利现值的计算公式为
P=F×(1+i)-n
其中,(1+i)-n通常称为“一次性收付款项现值系数”,用符号(P/F,i,n)表示,可以直接查阅附录B复利现值系数表。
【例3-3】 某企业进行一项投资,预计5年后可获得收益200万元,按年利率(折现率)10%计算,这笔收益的现值为
P=F×(1+i)-n=F×(P/F,i,n)
=200×(1+10%)-5万元=200×(P/F,10%,5)万元
=200×0.621万元=124.2万元
(二)年金终值与现值的计算
年金是指一定时期内每期等额收付的系列款项,通常记为A。年金的形式多种多样,如折旧、保险费、养老金、租金、等额分期收款、等额分期付款以及零存整取或整存零取储蓄等。年金按其每次收付发生的时点不同,可分为普通年金、即付年金、递延年金、永续年金等几种。
1.普通年金终值与现值的计算
1)普通年金终值的计算
普通年金是指从第一期起,在一定时期内每期期末等额发生的系列收付款项,又称后付年金。普通年金终值是指每期收付款项的复利终值之和,是折算到最后一期期末的本利和。
普通年金终值的计算公式为
F=A×(1+i)0+A×(1+i)1+A×(1+i)2+…
+A×(1+i)(n-2)+A×(1+i)(n-1)
整理上式,可得
![]()
其中,分式称为“年金终值系数”,记为(F/A,i,n),可通过直接查阅附录C年金终值系数表求得有关数值。
【例3-4】 某企业投资一项目,项目的建设期为5年,若5年内每年年末从银行借款50万元,借款年利率为10%,则该项目竣工时应付本息的总额为
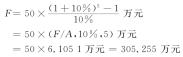
2)年偿债基金的计算
偿债基金是指为了在约定的未来某一时点清偿某笔债务或积聚一定数额的资金而必须分次等额形成的存款准备金。由于每次形成的等额准备金类似普通年金存款,因而同样可以获得按复利计算的利息,债务实际上等于普通年金终值,每年提取的偿债基金等于A。也就是说,偿债基金的计算实际上是普通年金终值的逆运算。其计算公式为
![]()
其中,![]() 称为“偿债基金系数”,记为(A/F,i,n),可直接查阅“偿债基金系数表”或利用年金终值系数的倒数推算出来。
称为“偿债基金系数”,记为(A/F,i,n),可直接查阅“偿债基金系数表”或利用年金终值系数的倒数推算出来。
【例3-5】 某企业有一笔5年后到期的借款,到期值为1500万元。若年利率为10%,则为偿还该项借款应建立的偿债基金为
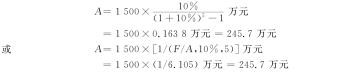
3)普通年金现值的计算
普通年金现值是指一定时期内每期期末等额收付款项的复利现值之和。其计算公式为
P=A×(1+i)-1+A×(1+i)-2+…+A×(1+i)-(n-1)+A×(1+i)-n
整理上式,可得
![]()
其中,![]() 称为“年金现值系数”,记为(P/A,i,n),可直接查阅附录D年金现值系数表求得有关数值。上式也可以写为
称为“年金现值系数”,记为(P/A,i,n),可直接查阅附录D年金现值系数表求得有关数值。上式也可以写为
P=A×(P/A,i,n)
【例3-6】 某企业租入某设备,每年年末需要支付租金1000元,年复利率为10%,则5年内应支付的租金总额的现值为
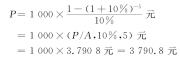
4)年资本回收额的计算
资本回收额是指在给定的年限内等额回收初始投入资本或清偿所欠债务的金额。年资本回收额的计算是年金现值的逆运算。其计算公式为
![]()
其中,![]() 称为“资本回收系数”,记为(A/P,i,n),可直接查阅“资本回收系数表”或利用年金现值系数的倒数求得。上式也可写为
称为“资本回收系数”,记为(A/P,i,n),可直接查阅“资本回收系数表”或利用年金现值系数的倒数求得。上式也可写为
A=P×(A/P,i,n) 或 A=P×[1/(P/A,i,n)]
【例3-7】 某企业现借款1000万元,用于新产品开发,在5年内以年利率12%等额偿还,则每年应付的金额为

【技能指引】 复利计算及其关系图解(见图3-1)。
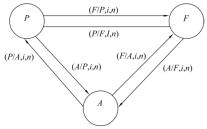
图3-1 复利计算及其关系图解
2.即付年金的终值与现值
即付年金是指从第一期起,在一定时期内每期期初等额收付的系列款项,又称先付年金。它与普通年金的区别仅在于付款时间的不同。
1)即付年金终值的计算
n期即付年金终值与n期普通年金终值的关系如图3-2所示。
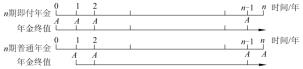
图3-2 即付年金终值与普通年金终值的关系
即付年金终值是其最后一期期末的本利和,是各期收付款项的复利终值之和。
从图3-2可以看出,n期即付年金与n期普通年金的付款次数相同,但由于其付款时间不同,n期即付年金终值比n期普通年金终值多计算一期利息。因此,在n期普通年金终值的基础上乘以(1+i)就是n期即付年金终值。其计算公式为
![]()
其中,![]() 称为“即付年金终值系数”,它是在普通年金终值系数的基础上,期数加1,系数值减1所得的结果。通常记为[(F/A,i,n+1)-1]。这样,查阅“1元年金终值系数表”得到(n+1)期的值,然后减去1便可得出对应的即付年金系数的值。这时即付年金的终值为
称为“即付年金终值系数”,它是在普通年金终值系数的基础上,期数加1,系数值减1所得的结果。通常记为[(F/A,i,n+1)-1]。这样,查阅“1元年金终值系数表”得到(n+1)期的值,然后减去1便可得出对应的即付年金系数的值。这时即付年金的终值为
F=A×[(F/A,i,n+1)-1]
【例3-8】 某企业在未来5年每年年初支付厂房租金10000元,银行存款利率为5%。则该企业期满后支付租金的本利和为
F=A×[(F/A,i,n+1)-1]
=10000×[(F/A,5%,6)-1]元
=10000×(6.802-1)元=58020元
2)即付年金现值的计算
n期即付年金现值与n期普通年金现值的关系如图3-3所示。
从图3-3可以看出,n期即付年金现值与n期普通年金现值的期限相同,但由于其付款时间不同,n期即付年金现值比n期普通年金现值少折现一期。因此,在n期普通年金现值的基础上乘以(1+i),便可求出n期即付年金的现值。其计算公式为
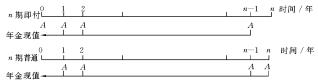
图3-3 即付年金现值与普通年金现值的关系
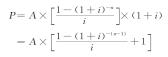
其中,![]() 称为“即付年金现值系数”,它是在普通年金现值系数的基础上,期数减去1,系数加上1所得的结果。通常记为[(P/A,i,n-1)+1]。这样,通过查阅“1元年金现值系数表”中(n-1)期的值,然后加上1,便可得出对应的即付年金现值系数的值。这时即付年金的现值为
称为“即付年金现值系数”,它是在普通年金现值系数的基础上,期数减去1,系数加上1所得的结果。通常记为[(P/A,i,n-1)+1]。这样,通过查阅“1元年金现值系数表”中(n-1)期的值,然后加上1,便可得出对应的即付年金现值系数的值。这时即付年金的现值为
P=A×[(P/A,n-1)+1]
3.递延年金终值与现值的计算
递延年金是指第一次收付款发生在第二期或第二期以后的年金(假设为m期,m≥1),它是普通年金的特殊形式,凡不是从第一期开始的普通年金都是递延年金。递延年金与普通年金的关系如图3-4所示。
![]()
图3-4 递延年金现值计算图
【例3-9】 某企业现在进行一项目投资,项目的建设期为5年,5年后该项目可连续8年为企业取得收益100万元,若年利率为10%,则此项目取得的收益的终值和现值应是多少?
1)递延年金终值的计算
由图3-4可以看出,该项目取得收益的形式属于递延年金,其中递延期(用m表示)为建设期5年,款项收付期(用n表示)为8年。而递延年金终值的计算方法和普通年金终值的类似,与递延期无关,则例3-9收益的终值应为
D=100×(F/A,10%,9)万元
=100×11.436万元=1143.6万元
2)递延年金现值的计算
第一种,先求出递延年金在n期期初(m期期末)的现值,再将它作为终值贴现至m期期初,即求出递延年金的现值。其计算公式为
![]()
例3-9中,有
P=100×(P/A,10%,8)×(P/F,10%,5)万元
=100×5.335×0.621万元=331.304万元
第二种,先求出(m+n)期普通年金现值,再减去没有付款的前m期普通年金现值,二者之差为递延m期后n期普通年金的现值。其计算公式为
![]()
例3-9中,有
P=A×[(P/A,10%,13)-(P/A,10%,5)]万元
=100×(7.103-3.791)万元=331.2万元
4.永续年金现值的计算
永续年金是指无期限等额收付的特种年金,可视为普通年金的特殊形式,即期限趋于无穷的普通年金。由于永续年金持续期无限,没有终止的时间,因此没有终值,只有现值。可由普通年金现值计算公式推导出永续年金现值的计算公式为
![]()
【例3-10】 某企业建立一项永久性的奖励基金,每年颁发20万元奖金,若年利率为5%,则现在应存入的资金是多少?
应存入的资金为
![]()
(三)资金时间价值计算中的几个特殊问题
1.利息率(折现率)的推算
对于一次性收付款项,根据其复利终值(或现值)的计算公式可得利息率的计算公式为
i=(F÷P)1÷n-1
对于永续年金,根据永续年金现值公式可得利息率的计算公式为
i=A÷P
普通年金利息率的推算比较复杂,无法直接套用公式,而必须利用有关的系数表,有时还要用到内插法。下面着重介绍利息率的推算方法。
(1)根据普通年金终值F、年金现值P的计算公式推算出年金终值系数(F/A,i,n)和年金现值系数(P/A,i,n)的计算公式分别为
(F/A,i,n)=F÷A, (P/A,i,n)=P÷A
(2)根据“年金终值系数表”或“年金现值系数表”,查找所计算的年金终值系数或年金现值系数。
(3)若在表所示的n期所对应的系数中找到所计算的年金终值系数或年金现值系数,则其对应的利息率就是所求的利息率i。
(4)若在表所示的n期所对应的系数中找不到所计算的年金终值系数或年金现值系数,则找出左右最临近的两个系数值,再用内插法计算所求的利息率i。
【例3-11】 某企业第一年年初投资55.275万元购置设备两台,投入即可使用,使用期6年,在使用期内每年为企业创造收益15万元,则该设备的投资收益率为多少?
依据题意,根据普通年金复利现值计算公式P=A×(P/A,i,n),得
55.275=15×(P/A,i,6)→(P/A,i,6)=3.685
查找“普通年金现值系数表”的n=6一行,恰好找到系数值为3.685,其所对应的利率为16%,则所求收益率为16%。
【例3-12】 某企业第一年年初投资45万元购置设备两台,投入即可使用,使用期6年,在使用期内每年为企业创造收益15万元,其投资收益率为多少?依据题意,根据普通年金复利现值计算公式P=A×(P/A,i,n),得
45=15×(P/A,i,6)→(P/A,i,6)=3
查找“普通年金现值系数表”的n=6一行,无法找到恰好为3的系数值,于是在该行中找到大于和小于3的两个最临界的系数值,即分别为3.326(i=20%)和2.951(i=25%),再利用内插法计算所求的收益率i,即
![]()
根据上述图示,按利率与相关系数呈线性相关,求得
![]()
2.期间的推算
在资金时间价值的计算中,已知终值、现值、利率、年金等变量,便可以根据终值(现值)的计算公式求出期间n,这一过程称为期间的推算。期间n的推算,其原理及其各步骤与利息率的推算相类似。
【例3-13】 某企业第一年年初投资45万元购置设备两台,投入即可使用,在使用期内每年为企业创造收益15万元,若年利率为10%,则该设备至少使用多少年才合算?
依据题意,根据普通年金复利现值计算公式P=A×(P/A,i,n),得
45=15×(P/A,10%,n)→(P/A,10%,n)=3
查找“普通年金现值系数表”的i=10%一列,无法找到恰好为3的系数值,于是在该列中找到大于3和小于3的两个最临界的系数值,即分别为2.487(n=3)和3.170(n=4),再利用内插法计算所求的期间n,即
![]()
根据上述图示,按利率与相关系数呈线性相关,求得
![]()
3.名义利率与实际利率
上面讨论资金时间价值时,均假定利率为年利率且每年复利一次。但实际上,复利的计息期间不一定是一年,有可能是季度、月份或日。例如,某些债券半年计息一次,有的抵押贷款每月计息一次,银行之间拆借资金均为每天计息一次。当每年复利次数超过一次时,这样的年利率称为名义利率,而每年只复利一次的利率才是实际利率。
对于一年内多次复利的情况,可采取两种方法计算资金时间价值。
第一种方法,将名义利率调整为实际利率,然后按实际利率计算资金时间价值。其计算公式为
i=(1+r÷m)m-1
其中,i为实际利率;r为名义利率;m为每年复利的次数。
【例3-14】 某企业存在银行的一笔资金为10万元,年利率为5%,每季度复利一次,到第5年年末的本利和是多少?
依据题意,P=10,r=5%,m=4,n=5,有
i=(1+5%÷4)4-1=5.09%
F=10×(1+5.09%)5万元=12.82万元
第二种方法,将名义利率r调整为每年复利周期一次时的利率r÷m,设复利基数为n年,则总的复利次数为m×n。
【例3-15】 利用例3-14的数据,求得
F=10×(1+5%÷4)4×5万元=12.82万元
第三节 风险与收益分析
一、风险的含义与特征
(一)风险的含义
上节所提出的资金时间价值是在不存在风险和没有通货膨胀条件下的投资报酬。这仅仅是一种假定而已。企业在经济活动中会面临诸多风险,如企业产品市场的价格风险、原材料供应市场的价格风险、国际金融汇率波动的风险以及证券利率的风险等。也就是说,风险是一种客观经济现象,是客观存在的,财务管理应充分考虑风险问题。
风险本身具有一种不确定性。在风险存在的情况下,只能事先估计到采取某种行动可能导致的结果,以及每种结果出现的可能性,而行动的真正结果究竟会怎样,不能事先确定。例如,用10000元购买1年期利率为4%的国库券,1年后的收益是400元,由于国库券的无风险性,事先就可确定1年后的收益。但若将10000元去购买某公司的股票,则无法事先确定1年后的收益,即购买股票的行为将面临风险。
总之,某一行动的结果具有多种可能而不肯定,就称有风险。反之,若某一行动的结果很肯定,就叫没有风险。从财务管理的角度看,风险是指企业在各项财务活动过程中,由于各种难以预料或无法控制的因素作用,企业的实际收益与预计收益发生背离,从而有蒙受经济损失的可能性。
(二)风险的特征
风险是企业财务管理环境的一个重要特征,财务管理的每一个环节都不可避免地要面对风险,企业在经营活动中,要强化风险意识。要有效地控制风险,就必须针对不同的情况研究风险的特征。风险的特征是风险内涵的反映,主要包括以下方面。
1.风险的客观性
风险是由客观存在的自然现象和社会现象引起的,它并不因人的意志而转移。企业在经营活动中无处不存在各种各样的风险,但可以认识和利用这些经济现象中的内在规律,科学地预测和决策,有效地控制风险,努力减少风险所造成的损失,但风险本身是不能消除的。
2.风险的偶然性
从人类社会发展看,风险是一种客观存在的、普遍的现象,风险的发生具有其必然性。但对个体风险而言,风险的发生是偶然的,其发生的原因、发生的时间等都有不确定性。正是风险的偶然性,在面对风险时,一方面要处理好风险可能造成的损失;另一方面要有计划地提取减值准备金。
3.风险的可测性
风险可以根据大量可靠的统计资料,以统计频率代替未知风险发生的真实概率;以主观概率进行有效的定量分析,运用科学的方法准确地估计和测算风险损失。
二、风险的分类与分散
(一)风险的分类
风险可以从不同的角度进行分类。
(1)从个别理财主体的角度看,风险可分为市场风险和企业特有风险两类。
①市场风险,又称为系统风险或不可分散风险,是指那些影响所有企业的风险,如国家宏观经济的调控政策、国际金融市场利率的波动、自然灾害、经济衰退、通货膨胀等。这类风险不能通过多元化投资来分散,涉及所有的证券,是投资者进行投资所必须承担的风险。
②企业特有风险,又称为可分散风险或非系统风险,是发生于个别企业的特有事项造成的风险,如罢工、诉讼失败、失去销售市场等。这类事件是随机发生的,可以通过多元化投资来分散。
(2)从企业本身来看,按风险形成的原因可将企业特有风险进一步分为经营风险和财务风险两大类。
①经营风险,是指生产经营方面的原因给企业盈利带来的不确定性。企业生产经营活动中会受到来源于企业外部和内部的诸多因素的影响,具有很大的不确定性。例如,原材料供应价格的市场波动、产品销售的波动、成本费用的变动、生产技术水平的不稳定、产品更新时期的把握、新产品研发的成败等。总之,所有这些生产经营过程中所面临的不确定性,都会引起企业收益的高低变化。
②财务风险,又称筹资风险,是指由于举债而给企业财务成果带来的不确定性。企业举债经营,全部资金中除自有资金外还有一部分借入资金,这会对自有资金的盈利能力造成影响;同时,借入资金需还本付息,到期无力偿付债务,企业便会陷入财务困境甚至破产。当企业息税前资金利润率高于借入资金利息率时,用借入资金获得的利润除了补偿利息外还会有剩余,因而自有资金利润率被提高了。但是,若企业息税前资金利润率低于借入资金利息率,则使用借入资金获得的利润就会不够支付利息,还需动用自有资金的一部分利润来支付利息,从而自有资金利润率就会降低。如果企业息税前利润还不够支付利息,就要用自有资金来支付,使企业发生亏损。若企业亏损严重,财务状况恶化,丧失支付能力,就会出现无法还本付息甚至会面临破产的危险。总之,财务风险的管理关键是要保证有一个合理的资金结构,维持适当的负债水平,既要充分利用举债经营这一手段获取财务杠杆收益,提高自有资金盈利能力,同时要注意防止过度举债而加大财务风险,避免陷入财务危机。
【知识链接】 雷曼兄弟破产事件
雷曼兄弟控股公司于1850年创办,是一家国际性金融机构及投资银行,环球总部设在美国纽约市,地区总部则位于伦敦及东京,在世界各国均设有办事处。该公司曾在全球范围内建立创造新颖产品、探索最新融资方式、提供最佳优质服务的良好声誉。2008年被美国《财富》杂志选为财富500强公司之一,为美国第四大投资银行。
2008年9月15日,该公司在次级抵押贷款市场危机(次贷危机)的强烈冲击下,在财务方面发生重大亏损而宣布申请破产保护。此时其负债高达6130亿美元,成为美国金融业最大的一宗公司破产案。
(二)风险的分散
非系统风险又称企业特有风险或可分散风险,是可以通过资产组合而分散掉的风险。它是指某种特定原因对某特定资产收益率造成影响而带来的不确定性。它是特定企业或特定行业所特有的,与政治、经济和其他影响所有资产的市场因素无关。企业特有风险可进一步分为经营风险和财务风险两大类。经营风险分散策略是企业通过开展多种风险活动,或者将高风险活动与低风险活动进行恰当组合,以使总体风险分散到各个项目的策略。企业具有一定的人、财、物资源优势,可通过多种经营活动的优化组合,在资源优化配置的同时,有效地分散风险,使多项经营活动的风险总和小于单一经营活动或经营形成的总体风险。财务风险分散策略是基于现代投资组合理论,在有效分散风险的同时最大限度地获取收益,以达到最优资源配置的目的,从而有利于实现财富最大化的策略。其主要指采取多元化经营、多方投资、多方筹资、争取多方客户等分散风险的方式。“不要把所有的鸡蛋都放在一个篮子里”形象地说明了进行多元化投资与经营对分散财务风险的作用。实务中常见的组合方法有多样化经营、联合经营、兼并与合并以及货币组合等,但多元化并不是万能的,如果不切实际地涉足过多产品或项目,主业不突出,这不仅不能分散风险,反而会使企业很难兼顾,更加被动。进行多元化投资与经营通常适用于财力雄厚、技术和管理水平较高的大型企业。
三、单项资产风险与收益
单项资产风险与收益是假设投资者仅持有一项资产的情况下所面临的风险与投资收益。要做好财务管理工作,就必须弄清不同风险条件下投资报酬率之间的关系,掌握风险报酬的计算方法。
(一)确定概率分布
在现实生活中,某一事件在完全相同的条件下可能发生也可能不发生,既可能出现这种结果又可能出现那种结果,这类事件称为随机事件。如果把所有可能的事件或结果都列示出来,且每种结果都赋予相应的概率,把它们列示在一起,便构成了概率的分布。概率就是用百分数或小数来表示随机事件发生的可能性及出现某种结果可能性大小的数值。
概率分布必须符合下列两个要求。
(1)所有的概率Pi都在0和1之间,即0≤Pi≤1。
(2)所有结果的概率之和应等于1,即![]() ,这里,n为可能出现结果的个数。
,这里,n为可能出现结果的个数。
【例3-16】 某企业现有A、B两个投资项目,预计项目投产后的收益情况与市场状况有关,A、B项目的预计收益和概率分布分别如表3-1、表3-2所示。
表3-1 A项目的概率分布 单位:万元

表3-2 B项目的概率分布 单位:万元

将随机事件各种可能的结果按一定的规则进行排列,同时列出各结果出现的相应概率,这一完整的描述称为概率分布。概率分布有两种类型。一种是离散型分布,又称不连续的概率分布,即对于随机变量和相对应的概率只取有限个数值,在坐标图中表现为概率分布在各个特定的点(见图3-5)上;另一种是连续型分布,即对所有的随机变量和对应的概率都予以估计,并且在坐标图中描述出来时表现为曲线,概率分布在相应的两点区间(见图3-6)上。
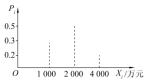
图3-5 离散型概率分布
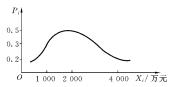
图3-6 连续型概率分布
(二)计算期望报酬率
期望值是一个概率分布中的所有可能结果,以各自相应的概率为权数计算的加权平均值,是加权平均的中心值,通常用符号E表示,其计算公式为
E=∑XiPi
【例3-17】 根据例3-16的资料计算A、B两项目预计收益的期望值。
EA=(4000×0.2+2000×0.5+1000×0.3)万元=2100万元
EB=[5000×0.2+2800×0.5+(-1000)×0.3]万元=2100万元
预计收益的期望值反映了预计收益的平均化,在各种不确定性因素的影响下,它代表投资者的合理预期。例3-17中A、B两个项目的预期收益相等,说明两个项目平均收益是相同的,但其概率分布不同,A项目预计收益的分散程度小,B项目预计收益的分散程度大,这说明两个项目的预期收益值相等,但风险不同。为了定量地衡量风险的大小,还要使用统计学中衡量概率分布离散程度的指标。
(三)计算离散程度
离散程度是用于衡量风险大小的统计指标。反映随机变量离散程度的指标包括平均差、方差、标准离差、标准离差率和全距等。下面主要介绍方差、标准离差和标准离差率三项指标。一般来说,离散程度越大,风险越大;离散程度越小,风险越小。
1.方差
方差是偏差平方和以概率为权数的加权平均数,用来表示随机变量与期望值之间离散程度的一个数值。其计算公式为
σ2=∑(Xi-E)2×Pi
【例3-18】 根据例3-16的资料计算A、B两项目预计收益的方差,即
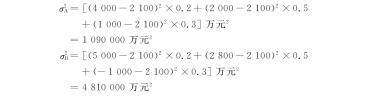
2.标准离差
标准离差也称均方差,是方差的算术平方根,其计算公式为
![]()
标准离差以绝对数衡量决策方案的风险,在期望值相同的情况下,标准离差越大,风险越大;反之,标准离差越小,则风险越小。
【例3-19】 根据例3-16的资料计算A、B两项目预计收益的标准离差,即

由上述计算结果可以看出,A项目预期收益的取值较为集中,B项目预期收益的取值较为分散,故一定程度上反映了B项目的风险较大。
3.标准离差率
标准离差率是标准离差同期望值之比,通常用符号q表示,其计算公式为
![]()
标准离差率是一个相对指标,它以相对数反映决策方案的风险程度。方差和标准离差作为绝对数,只适用于期望值相同的决策方案风险程度的比较。对于期望值不同的决策方案,评价和比较其各自的风险程度时只能借助于标准离差率这一相对数值。在期望值不同的情况下,标准离差率越大,风险越大;反之,标准离差率越小,风险越小。
【例3-20】 现仍根据例3-16的资料计算A、B两项目预计收益的标准离差率,即
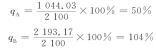
由上述计算结果可以看出,A项目预期收益的标准离差率小,风险小;B项目预期收益的标准离差率大,风险大。
(四)计算风险报酬率
标准离差率虽然能评价投资风险程度的大小,但它还不是风险报酬率。要计算风险报酬率,还必须借助一个系数。风险报酬率、风险报酬系数和标准离差率之间的关系为
RR=b×q
其中,RR为风险报酬率;b为风险报酬系数;q为标准离差率。
那么,投资总报酬率可以表示为
K=RF+RR=RF+b×q
其中,K为投资总报酬率;RF为无风险报酬率。
无风险报酬就是加上通货膨胀贴水以后的货币时间价值,是指最低的社会平均报酬。可将国库券的报酬率和短期公债利率视为无风险报酬率。
风险报酬系数是将标准离差率转化为风险报酬的一种系数。风险报酬系数的确定方法有以下几种。
(1)根据同行业、同类项目的历史资料,利用公式K=RF+RR=RF+b×q,得
![]()
(2)由企业的决策者或行业组织及专家小组来确定。
(3)由国家有关部门组织专家确定。
由上述可知,投资者可以对风险加以量化,也可以据此推算出风险的报酬率,然后对投资作出正确的决策。对于单个方案,决策者可根据其标准离差(率)的大小,并将其与设定可接受的此项指标最高限值对比,看前者是否低于后者,然后进行取舍。对于多方案择优,决策者的行动准则应是选择低风险高收益的方案,即选择标准离差最低、期望收益最高的方案。然而高收益往往伴有高风险,低收益方案其风险程度往往也较低,究竟选择何种方案,就要权衡期望收益与风险,而且还要视决策者对风险的态度而定。对风险比较反感的人可能会选择期望收益较低同时风险也较低的方案,喜欢冒风险的人则可能选择风险虽高但收益也高的方案。
四、组合资产风险与收益
(一)组合资产
企业在生产经营过程中应该综合考虑各种资产的风险与报酬之间的联系,寻求将风险分散化的可能途径,即将两种或两种以上资产进行多方位的组合,称为组合资产。如果组合资产中的资产均是有价证券,则该组合资产就称为组合证券。
(二)组合资产的预期收益率
组合资产的预期收益率是组合资产中单项资产期望收益率以投资比重为权数的加权平均数,其计算公式为
![]()
其中,E(Rp)为组合资产期望收益率;Wi为第i项资产在投资组合总体中所占比重;Ri为第i项资产的期望收益率;n为组合资产的个数。
【例3-21】 某投资组合中有A、B两种资产,期望收益率分别为10%、15%,若投资者把40%的资金投向A,60%的资金投向B,则该组合资产的期望收益率为
E(Rp)=10%×40%+15%×60%=13%
(三)组合资产风险的度量
1.两项组合资产的风险
组合资产收益率方差通常包含三个变量,即每种资产的收益率、风险(方差或标准差)及相关系数。两种资产组合而成的投资组合收益率方差的计算公式为
![]()
其中,σp为组合资产的标准差;w1、w2分别为资产1和资产2在投资组合总体中所占比重;σ1、σ2分别为两种资产的标准差;ρ1,2反映两项资产收益率的相关程度,即两项资产收益率之间相对运动的状态,称为相关系数,理论上该系数介于-1 和1之间。
当ρ1,2=1时,两项资产的收益率具有完全正相关的关系,即它们的收益率变化方向和变化幅度完全相同,这时![]() 达到最大。说明两项资产正相关时风险不能抵消,这样的组合资产不能降低任何风险。
达到最大。说明两项资产正相关时风险不能抵消,这样的组合资产不能降低任何风险。
当ρ1,2=-1时,两项资产的收益率具有完全负相关的关系,即它们的收益率变化方向和变化幅度完全相反,这时![]() 达到最小。说明两项资产负相关时二者的风险可以相互抵消,甚至完全消除。这样的组合资产可以最大限度地抵消风险。
达到最小。说明两项资产负相关时二者的风险可以相互抵消,甚至完全消除。这样的组合资产可以最大限度地抵消风险。
在实际工作中,两项资产的收益率具有完全正相关和完全负相关的情况几乎不可能。绝大多数资产两两之间都具有不完全相关的关系,即相关系数小于1且大于-1(多数情况下大于0)。因此0<σp<(w1×σ1+w2×σ2),即组合资产的标准差小于组合中各资产标准差的加权平均值,因此,组合资产可以分散风险,但不能完全消除风险。
2.多项资产组合的风险
一般来讲,随着资产组合中资产个数的增加,资产组合风险会逐渐降低,当资产的个数增加到一定程度时,资产组合风险程度将趋于平稳,这时组合风险的降低将非常缓慢直到不再降低。
随着资产组合中资产数目的增加,由方差表示的各资产本身的风险状况对组合风险的影响逐渐减小,乃至于最终消失。但由协方差表示的各资产收益率之间相互作用、共同运动所产生的风险并不能随着组合中资产个数的增加而消失,它是始终存在的。
那些只反映资产本身的特性,也就是组合资产可通过增加组合中资产数目而最终消除的风险称为非系统风险。那些反映资产之间相互关系,共同运动,无法最终消除的风险称为系统风险。
3.资本资产定价模型
资本资产定价模型CAPM由经济学家威廉·夏普(William F.Sharpe)、约翰·林特纳(John Lintner)于20世纪60年代提出,广泛地应用于资产组合特别是证券组合投资系统风险和收益确认上。
资本资产定价模型的表达式为
kF=RF+β×(kE-RF)
其中,kF为投资组合的预期报酬率;RF为无风险报酬率;β为投资组合的系统风险指数,即某资产的市场风险相对于全部资产市场风险的倍数;kE为市场平均报
酬率;(kE-RF)为市场平均风险报酬率;β×(kE-RF)为投资组合的预期风险报酬率。
【例3-22】 某企业持有甲、乙、丙三种股票构成投资组合,它们的β系数分别为0.5、1.0、2.0,在投资组合中所占比重分别为20%、30%、50%,证券市场的平均报酬率为10%,无风险报酬率为5%,计算该投资组合的系统风险指数和预期报酬率分别为
β=∑wjβj=0.5×20%+1.0×30%+2.0×50%=1.40
kF=RF+β×(kE-RF)=5%+1.40×(10%-5%)=12%
从上述计算可得如下结论。
①该证券组合投资的β系数为1.40,说明其风险是整个市场风险的1.4倍。
②证券市场的平均风险报酬率为5%(10%-5%),而该证券组合的风险报酬率为7%(1.40×5%)。
③该证券组合投资的预期报酬率为12%(5%+7%)。
资本资产定价模型也可用图形表示,即用所谓证券市场线(Security Market Line,简称SML)来表示,例3-22的资本资产定价模型如图3-7所示。

图3-7 证券市场线
复习思考题
1.解释下列名词术语:
资金时间价值 年金 普通年金 即付年金
系统风险 非系统风险 经营风险 财务风险
2.什么是财务估价?估价的计量标准有哪些?
3.终值、现值的含义是什么?
4.复利的终值与现值如何计算?
5.如何计算预付年金、递延年金的终值与现值?
6.偿债基金系数与普通年金终值系数、资本回收系数与普通年金现值系数的关系是什么?为什么?
7.对于一年内多次复利的情况,如何将名义利率调整为实际利率?
8.风险的定义是什么?具有哪些特征?如何进行分类?
9.简述风险度量指标。
10.风险报酬的含义是什么?风险与报酬的关系是怎样的?
练习题
一、单项选择题
1.某企业于年初存入银行10000元,假定年利率为12%,每年复利两次,则第5年末的本利和为( )元。
A.13382
B.17623
C.17908
D.31058
2.在下列各项资金时间价值系数中,与资本回收系数互为倒数关系的是( )。
A.(P/F,i,n)
B.(P/A,i,n)
C.(F/P,i,n)
D.(F/A,i,n)
3.如果A、B两种证券的相关系数等于0.8,A的标准离差为18%,B的标准离差为10%,投资比率为0.6和0.4,则该证券组合的标准离差等于( )。
A.14.80%
B.14.20%
C.11.84%
D.14%
4.已知甲方案投资收益率的期望值为15%,乙方案投资收益率的期望值为12%,两个方案都存在投资风险,比较两方案风险大小应采用的指标是( )。
A.方差
B.净现值
C.标准离差
D.标准离差率
5.根据资金时间价值理论,在普通年金现值系数的基础上,期数减1,系数加1的计算结果应当等于( )。
A.递延年金现值系数
B.后付年金现值系数
C.预付年金现值系数
D.永续年金现值系数
6.某企业向银行借款100万元,年利率为10%,半年复利一次,则该借款的实际利率是( )。
A.10%
B.5%
C.11%
D.10.25%
7.有一项年金,前3年无流入,后5年每年年初流入500万元,假设年利率为10%,其现值为( )万元。
A.1994.59
B.1565.68
C.1813.48
D.1423.21
8.关于标准离差和标准离差率,下列表述正确的是( )。
A.标准离差是各种可能报酬率偏离预期报酬率的平均值
B.如果以标准离差评价方案的风险程度,则标准离差越小,投资方案的风险越大
C.标准离差率即风险报酬率
D.对比期望收益率不同的各个投资项目的风险程度,应使用标准离差率
9.某人拟在5年后用20000元购买一台计算机,银行年复利率为12%,此人
现在应存入银行( )元。
A.12000
B.13432
C.15000
D.11348
10.A方案在3年中每年初付款100元,B方案在3年中每年末付款100元,若利率为10%,则两者在第3年末的终值相差( )元。
A.33.1
B.31.3
C.133.1
D.13.31
11.假设以8%的年利率借得50000元投资于某个寿命期为5年的项目,为使得项目成为有利可图的项目,每年本利的收回额至少为( )元。
A.10000
B.12522.9
C.12052.7
D.13120.8
二、多项选择题
1.在下列各种情况下,会给企业带来经营风险的有( )。
A.企业举债过度
B.原材料价格发生变动
C.企业产品更新换代周期过长
D.企业产品的质量不稳定
2.下列关于资金时间价值的表述,正确的有( )。
A.资金时间价值是资金经过投资和再投资增加的价值
B.资金时间价值必须按复利方式计算
C.资金时间价值是一种客观存在的经济现象
D.资金时间价值是指没有风险和没有通货膨胀条件下的社会平均资金利润率
3.下列因素引起的风险中,可以分散的有( )。
A.通货膨胀
B.某公司工人罢工
C.公司在市场竞争中失败
D.新产品开发失败
4.风险报酬的种类包括( )。
A.通货膨胀补偿
B.期限风险报酬
C.流动性风险报酬
D.违约风险报酬
5.反映随机变量离散程度的指标有( )。
A.期望值
B.方差
C.标准离差
D.标准离差率
6.下列表述中,正确的有( )。
A.复利终值系数和复利现值系数互为倒数
B.普通年金终值系数和普通年金现值系数互为倒数
C.普通年金终值系数和偿债基金系数互为倒数
D.普通年金现值系数和投资回收系数互为倒数
7.A项目的确定报酬率为10%;B项目的报酬率有两种可能:一是有50%的可能性获得30%的报酬率;二是有50%的可能性亏损10%的报酬率,则下列说法正确的有( )。
A.B项目的期望收益率为10%
B.A项目风险小于B项目风险
C.投资者绝不可能选择B项目
D.投资B项目获得的实际报酬可能大大超过A项目的
三、判断题
1.1元钱按8%计单利,200年后的终值是17元,而若复利计,则是4838949.59元。( )
2.利率为i、期限为n的预付年金现值,等于利率为i、期限为n-1的普通年金现值加该笔年金。( )
3.在复利条件下,预得整取求零存,是一个年偿债基金的计算问题;而已知整存求零取,则是一个年资本回收额的计算问题。( )
4.资金时间价值经常用利率来表示,所以,资金时间价值的实质就是利率。( )
5.对于多个投资方案而言,无论各方案的期望值是否相等,标准离差率最大的方案一定是风险最大的方案。( )
6.由于经营风险是指生产经营的不确定性带来的风险,是任何商业活动都有的,所以它是不可分散风险。( )
7.在现值及期限一定的情况下,利率越高,终值越大;在终值及期限一定的情况下,利率越高,现值越小。( )
8.各投资项目报酬率的期望值是否相同,都可以采用标准差比较其风险程度。( )
9.国库券是一种几乎没有风险的有价证券,其利率可以视为资金时间价值。( )
10.当每年复利次数超过一次时,给定的年利率称为名义利率。( )
四、计算分析题
1.ABC公司在2003年1月1日存入银行1000元,年利率为10%。要求:
(1)每年复利一次,2006年1月1日存款账户余额是多少?
(2)每季度复利一次,2006年1月1日存款账户余额是多少?
(3)分别在2003年、2004年、2005年、2006年1月1日存入250元,年利率仍为10%,每年复利一次,2006年1月1日余额是多少?
(4)假定分4年存入相等金额,为了达到第一问所得到的账户余额,每期应存入多少金额?
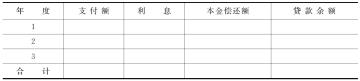
2.假定C公司贷款1000元,必须在未来3年每年底偿还相等的金额,而银行按贷款余额的6%收取利息。要求:编制如下还本付息表(保留小数点后2位)。
还本付息表 单位:元
3.A公司某项投资的资产利润率概率估计情况如下表所示。
资产利润率概率估计

假定该公司无负债,且所得税率为40%。要求:
(1)计算资产利润率的期望值;
(2)计算资产利润率的标准离差;
(3)计算税后资本利润率的标准离差;
(4)计算资产利润率的变异系数。
(计算结果百分数中,保留到2位小数,2位后四舍五入)
4.一项600万元的借款,借款期限3年,年利率为8%。要求:
(1)若每半年复利一次,年实际利率是多少?
(2)若每半年复利一次,年实际利率会高出名义利率多少?
5.A矿业公司决定将其一处矿产开采权公开拍卖,因此它向社会各煤矿企业招标开矿。已知甲公司和乙公司的投标书最具有竞争力,甲公司的投标书显示,如果该公司取得开采权,则从获得开采权的第1年起,每年末向A公司交纳10亿美元的开采费,直到10年后开采结束;乙公司的投标书表示,该公司在取得开采权时,直接付给A公司40亿美元,在8年后开采结束,再付给A公司60亿美元。如A公司要求的年投资回报率达到15%,应该接受哪个公司的投标?
6.某公司拟购置一处房产,房主提出两种付款方案:(1)从现在起,每年年初支付20万元,连续支付10次,共200万元。(2)从第5年开始,每年年初支付25万元,连续支付10次,共250万元。假设该公司的资本成本率(即最低报酬率)为10%,你认为该公司应选择哪种方案?
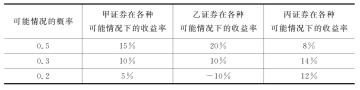
7.某公司拟在现有的甲证券的基础上,从乙、丙两种证券中选择一种风险小的证券与甲证券组成一个证券组合,资金比例为6∶4,有关资料见下表。要求:
(1)应该选择哪一种证券?
(2)假定资本资产定价模型成立,如果证券市场平均收益率为12%,无风险利率为5%,请计算所选择的组合的预期收益率和β系数。
甲、乙、丙三种证券的收益率预测信息
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。

















