第二节 长期负债概述
企业在生产经营的扩展阶段，往往需要筹集大量的长期资金来购建长期资产。企业经营所需长期资金的来源主要有两种途径：一是由业主追加投资或由公司通过增发股票向股东筹集资金；二是通过举借长期债务向债权人筹集资金。一般情况下，公司往往愿意采纳后一种途径，这样，如何举借长期债务则是企业管理当局必须要考虑的一项重要的财务决策。
一、长期负债的特征
长期负债是指偿还期限在一年或者超过一年的一个营业周期以上的债务。如企业长期贷款、应付公司债券、融资租赁等债款等。
长期负债具有两方面的重要特征：一是债务偿还期限较长。长期负债的偿还期一般在一年或者超过一年的一个营业周期以上，因此，对企业来说，长期负债是一种长期稳定的资金来源。二是债务的金额较大。企业举借长期债务主要是为了满足在扩展阶段购置机器设备等长期资产、进行扩大再生产所必要的投资，因而债务的金额通常都是比较大的。
二、长期负债的内容
长期负债一般包括以下内容：
(1)公司债券。公司债券是指公司为筹集长期资金而对外发行的一种有价证券，它是债券发行公司承诺在未来向债权人偿还债券本息的书面证明。
(2)长期借款。长期借款是指企业向银行或其他金融机构借入的偿还期在一年或者超过一年的一个营业周期以上的各项借款。由于长期借款通常是以借债企业的资产作为抵押品，并以票据形式取得，因此又称为应付长期抵押票据。
(3)其他长期负债。其他长期负债是指除应付公司债券和长期借款以外的其他各种长期负债，主要包括应付租赁负债、应付退休金等。
三、长期负债的确认和计量
长期负债的确认与流动负债一样，都是在企业成为负债交易合约一方的时候确认，在负债终止确认前都应在资产负债表上列报披露。一旦负债得以偿还、合约已经终止或负债已经转移，则应终止确认负债。由于长期负债偿还期较长，与流动负债计量有较大不同。
(一)长期负债的初始计量
长期负债的入账价值应按债务产生时的实际成本，即企业未来需要偿还的债务按现行市场利率折成的现值计价，如果发生相关交易费用，如支付给券商的佣金或手续费等，应计入初始确认金额。
(二)长期负债的后续计量
除特殊类别的长期负债外，一般来说，长期负债以摊余成本计量。摊余成本是指初始确认金额减去以偿还本金加上或减去尚未摊销的溢价或折价(溢价或折价是指负债初始确认金额与到期日金额之间的差额)。折价或溢价将在本章第三节介绍。
长期负债的每期利息费用应等于每期期初的实际负债余额乘以举债时的实际市场利率。
由于长期负债涉及利息率与现贴值计算，因此应了解货币时间价值的基本概念。
四、货币时间价值的有关概念
从经济学的观点看，即使在没有风险和通货膨胀的条件下，今天1元钱的价值应大于一年以后1元钱的价值。今天投资一笔货币，就放弃了使用或消费这笔货币的机会或权利，那么按放弃时间的长短而计算的代价或报酬就称为货币时间价值。
货币时间价值一般有两种表现形式：从相对量来看，就是在不考虑风险和通货膨胀条件下的社会平均投资报酬率；从绝对量来看，就是货币资本在生产经营过程中带来的真实增值额，即一定数额的货币资本与时间价值率的乘积。
在实际工作中，一般均以银行存款利息或利率反映或代表货币时间价值。通常将短期国库券的利率视同货币时间价值。在实务中，对利息的计算又有两种方式，一种是单利计算，另一种是复利计算。分析货币时间价值的影响，通常按复利计算。所谓复利是指在计算利息时，不仅本金计算利息，由本金产生的利息也应计息。本节所介绍的终值和现值的计算都是建立在复利计息基础上的。
(一)一次性收付款项的终值和现值的计算
在某一特定时点上发生的某项一次性付款(或收款)业务，经过一段时间后再发生相应的一次性收款(或付款)业务，称为一次性收付款项。例如，现在存入银行一笔1000元的现金，年利率为10%，经过4年后一次取出本利和1464.1元，就属于这类一次性收付款项。这里将n期后的本利和称为终值(FV)，也就是现在的某一金额按规定利率计算的未来价值；将存款当时的本金称为现值(PV)，也就是未来某一金额按规定利率折算的现在价值。
设现值为PV，终值为FV，年利率为i，复利期数为n，那么终值与现值有如下关系：
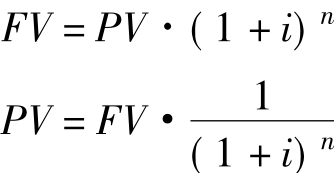
一次性收付款项的终值和现值一般又称为复利终值和复利现值。上式中的(1+i)n称为复利终值系数，记作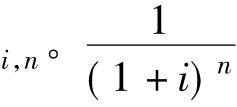
称为复利现值系数记作PVIFi，n。复利现值系数通常也称折现系数，所用的利率又称为折现率。
这样，上述计算复利终值和复利现值的计算公式可改写为：
FV=PV·FVIFi，n
PV=FV·PVIFi，n
在使用复利终值系数和复利现值系数时，可以不必用公式来计算，而根据i和n的具体数值，在1元复利终值系数表和1元复利现值系数表上直接查得(见附表一和附表二)。例如，利率为10%，复利期为3，在1元复利终值系数表上可查得复利终值系数为1.331；利率为10%，复利期为4，则在1元复利现值系数表上可查得复利现值系数为0.68301。这样通过现值和终值的计算，就可以把不同时间的货币置于同一可比的基础上。
【例7－11】假设某企业现在取得一笔贷款，3年后偿还现金100000元，贷款年利率为10%，3年后偿还贷款的现值是多少?
解决这个问题可以把3年后偿还按10%的利率折算为现值，查1元复利现值系数表得复利现值系数为0.75131。有关计算如下：
PV=FV·PVIF10%，3=100000×0.75131=75131元(元)
3年后偿还100000元现金的现值为75131元，即现在银行贷给企业的现金是75131元。
(二)年金的终值和现值的计算
所谓年金是指在一定时期内，每隔相同时间就发生相同数额的系列收款或付款，也称等额系列款项。例如，按期支付相同金额的保险费、租金、债券利息、优先股股息以及每年投入相等金额的款项或每年等额收回的投资额等，都属于年金的范畴。
年金按其收付款的具体方式不同，又分为普通年金、先付年金、递延年金和永续年金等几种形式，其中普通年金的应用最为广泛。
所谓普通年金是指发生于相同间隔期期末的系列等额收款或付款，也称后付年金。按一定利率计算的若干期普通年金的本利总和称为普通年金终值，简称年金终值；按一定利率将若干期普通年金折算到现在的价值总和称为普通年金现值，简称年金现值。
假定每年年末在银行存入100元，连续存4年，银行存款年利率为10%，每年复利一次。利用前述复利现值和复利终值的计算方法，该项系列存款的现值和终值的计算如图7－1所示。
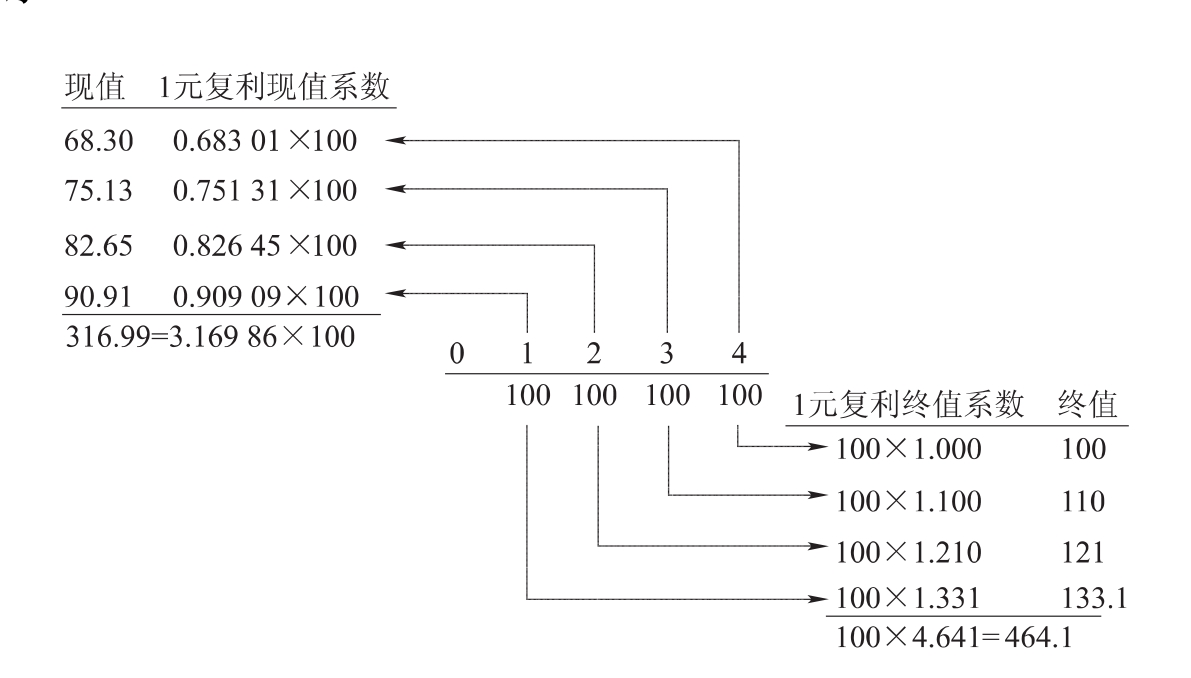
图7－1 年金现值和年金终值计算图
根据图7－1的计算原理，可推导出计算年金终值和年金现值的公式。设A为年金，FVA为年金终值，PVA为年金现值，i为年利率，n为计息期数。
根据图7－1，年金终值的计算公式为：
FVA=A+A(1+i)1+A(1+i)2+……+A(1+i)n－2+A(1+i)n－1
根据上式可推导出：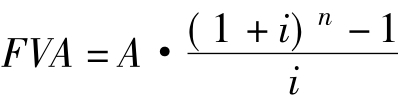
上式中，［(1+i)n－1］/i称为年金终值系数，记作FVIFAi，n，于是上式又可写成：
FVA=A·FVIFAi，n
根据图7－1，年金现值的计算公式为：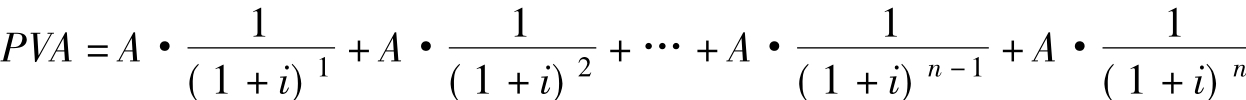
根据上式可推导出：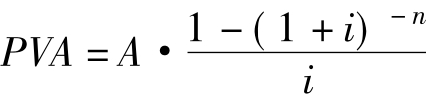
上式中，［1－(1+i)－n］/i称为年金现值系数，记作PVIFAi，n，于是上式又可写成：
PVA=A·PVIFAi，n
1元年金终值系数和1元年金现值系数也可以在1元年金终值系数表和1元年金现值系数表上直接查得(见附表三和附表四)。
【例7－12】假设某企业现在从银行取得一笔贷款，5年分期偿还，每年末还款100000元，贷款年利率为10%，5年偿还贷款的现值合计是多少?
年利率为10%，未来5年分期偿还。
根据题意，A=100000元，n=5，i=10%查表可得PVIFA10%，5=3.79079
PVA=A·PVIFA10%，5=100000×3.79079=379079(元)
即未来5年5次还款现值合计为379079元，即利率10%计算，现在银行给企业的贷款总额为379079元。
上述货币时间价值及贴现值计算方法将用于应付公司债券的发行等相关计算。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
