债券的投资收益率

第三节　债券的投资收益率

一、息票债券

本节将介绍一种债券，可称为“息票债券”(coupon bond)，债券通常指的是一年以上工具，息票债券即是每隔一段期间，持票人可将息票撕下，再到财政部指定的银行换取现金。美国公债的名称，一般是以年分类。见图5-6。

图5-6　美国公债分类

(一)息票债券的特征

(1)到期日通常超过1年。

(2)通常每半年支付一次利息，每次支付时，可撕下一张息票到财政部指定银行领息，如图5-7所示的C即为可撕的息票。

(3)在到期日，支付本金最后一次的利息。

就图5-7的公债，我们想了解财政部想借1 000万元(面值F)，每年支付一次利息(票息C)，共支付10年(到期日N)，其利率为8%(息票利率i_c)，则投资人愿出多少钱(购买价格P)买这一张公债?

图5-7　公债简例

债券价格P的公式为

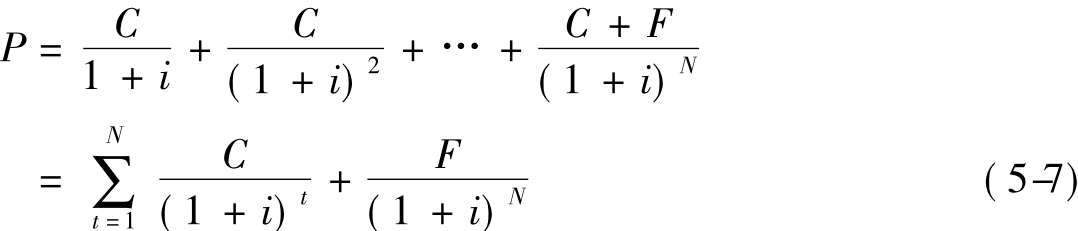
由于此公式的第一项即为本章第一节的固定贷款，故公式(5-7)可简化为

式中：

P：购买价格

C：票息

F：面值

N：支付次数

i：投资收益率

在本例中，假设投资人认为真正报酬率(即YTM)应不只8%，而为8.5%，则

练习题：

问：上题中，假设投资人认为市场利率为7.5%，则他愿付多少钱?

答：用快速公式

练习题：

问：如果上题的市场利率改为8%，则P=?

答：1 000万元。

(二)息票债券的价格与殖利率

由上述的两项练习题，可以得到债券价格与殖利率的关系。

重新整理上述的三个数字题目的F、i_C、P与YTM关系，如表5-1所示。

表5-1　　　　　　　　　　　　　债券价格与殖利率的关系

关系(1)：债券价格与殖利率(最接近市场利率)走势相反。

关系(2)：当面值F=售价P，则票面利率i_C=到期殖利率YTM，称为平价出售(sell at par)，故一般所谓“平价债券”，即指的是一张债券的面值等于售价。

这结论亦可以被证明如下：

将

C=i_C×F=i_C×P

及所有F改为P，再代回简易公式(5-8)，即可得知i_C=i=YTM

关系(3)：当

F＞P则i_C＜YTM(折价出售)

F＜P则i_C＞YTM(溢价出售)

不用数学推导，我们也可以由直觉判断关系(3)的方向。

以F＜P为例，这表示债券的售价高于面值，我们要问为什么投资人愿出较债券面值高的金额，购买此债券?其原因必定在于这张债券的支付期间所给的票息很高，当票息C很高，表示C=i_C×F的i_C很高，如果将关系(2)当一个比较基础，即F=P时，i_C=YTM，则当F＜P时，i_C应超过YTM。

因此对筹资的公司而言，如果想筹资10亿元，则不能将票面利息订得太低，否则将筹不到10亿元。上述的关系可以整理如下：

溢价出售i_C＞YTM

平价出售i_C=YTM

折价出售i_C＜YTM

练习题：

问：5年期的建设公债，面值100万元，以平价出售，2000年5月23日发行，至2005年5月23日到期，票面利率为5.75%，建设公债在发行满2年之后，每一年偿付本金的1/4，2000年5月的定期存款利率为8.0%。试问投资人值不值得买此公债?

答：

1=上一期(C)×5.75%

用i=8%代回：

53 240+263 631.69+232 692.08+204 889.57+179 929.18=934 382.52＜1 000 000

因此第一次用8%太小，而现值只有934 328。在不考虑风险、流动性的状况下，不值得买此公债。

上述的例子皆是给定YTM，再求价格P，也当然可以先给P，再反求YTM也可以。例如，1 000元的10年期债券，而面值利率i_C为10%，每年付息一次，则当售价为955元时，其到期殖利率YTM为多少?当求算YTM时，必须使用特殊的计算器，不过因为它是折价出售，故由关系(3)得知YTM＞i_C，此题的答案为10.75%。

二、折现债券

折现债券在到期日前不付任何利息，故不适合到期日太长。试想如果某人向你借钱，10年后才一次将本利和还你，或是每半年就付你一次利息，最后一次还利息也还本金，何者的还款方式较易被你接受?就前者言，因为10年后才一次还本利和，这段长期间，投资人未能与公司接触，是否会担心公司早已人去楼空?因此，投资人较愿接受后者而不愿接受长期的折现债券。

公司也通常不愿发行长期折价债，因为一张长期的折价债券，在今天筹资时，公司恐怕收不到多少钱，例如，N=3年，i=8%，面值100元的折现债券公司今天只能收到

故折价债券很少超过3年，且通常到期日小于1年，而到期日如果超过一年，称为“深折现债券”(deep discount bond)，表示售出时要大幅度折价。

三、永久年金

所谓年金(annuity)指的即是每一期固定有一笔收入，例如前述的固定贷款或息票债券的票息C是一种年金。

永久年金(consol)也称为永久债券(perpetual bond)是不但每一期有一笔固定收入，且此收入永不停止，即

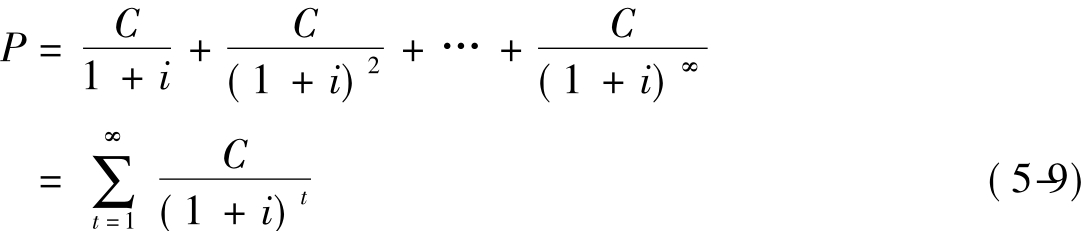
它也可简化成^[2]

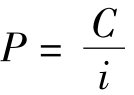
此时YTM=C/P，可以快速算出。

例如第一次世界大战时，英国决定发行永久年金，且言明只要英国存在一天，就会每年固定偿还10英镑，则英国人愿出多少钱买此债券?假设当时利率i=8%。

应用公式(5-10)：

故只要现在出125英镑，可永远向英国每年领10英镑。