短期汇率的决定

第三节　短期汇率的决定

短期汇率主要受到资金的流出流入影响，即资本项目影响汇率在短期的波动。让我们以无抛补利率平价说(uncovered interest rate parity)说明短期资本移动如何影响汇率。

假设某一投资人有100元，要投资3个月(投资期间)，并且他投资的标的可以有两个选择：他可以投资国内，也可以投资国外。假设投资这两个不同地方的报酬分别如下：

1.投资国内定期存款3个月

将100元存为国内定期存款，利率为i_t，3个月后领回本利和

100(1+i_t)　　　　　　　　　　　　(9-6)

i_t代表在t期(今天)的本国利率，在今天可以被观察到。见图9-1。

2.投资国外定期存款3个月

步骤1：先将100元人民币换成美元。得到

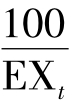
的美金。请注意EX_t的下标t，表示现在为t期。

步骤2：将此(100/EX_t)美元存放银行，3个月后，可得本利和

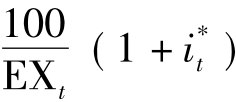
图9-1　投资国内3个月的报酬

式中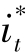代表的是在t期时的今天，可以被观察得到的外国利率。

步骤3：预期将3个月后的美元本利和转换成人民币

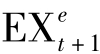的下标t+1期代表3个月后的汇率，而上标的e代表的是预期。由于投资者目前所处的位置是t期，他并不知道3个月后的汇率是多少，所以要预期3个月后的汇率，故加上e。

所以，步骤3的意义即是如果3个月后的汇率是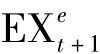，则届时我们将步骤2所得美元本利和转成人民币，可得到的预期人民币报酬。

另外，要将3个月后得到的美元本利和换回人民币，是因为我们在国内交易只使用一种货币，而不能同时使用两种货币，且只有均换成同一货币才能进行比较两者的报酬。

如果将投资国外画成图9-2，则更易理解。

当没有套利机会时，投资国内的报酬应等于(预期)投资国外的报酬，即式(9-6)=(9-7)，

右方最后一项同时加1减1，可得

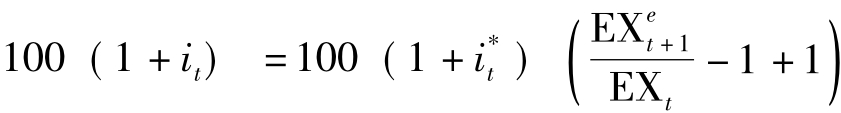
再删去100，可得

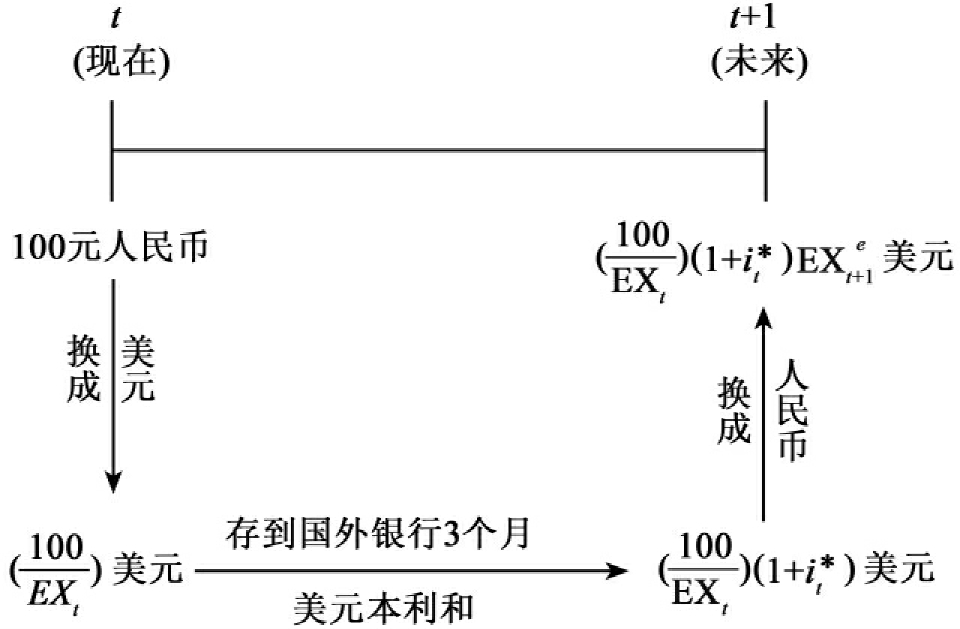
图9-2　投资国外3个月报酬

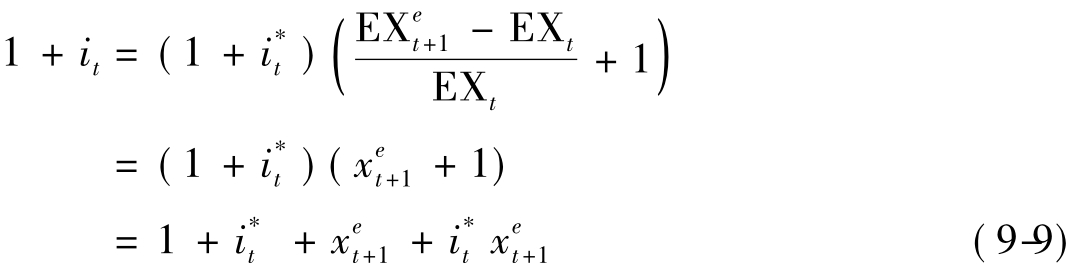
式中假设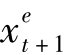代表

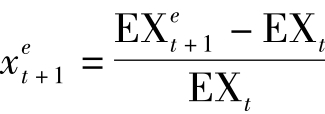
即是美元预期贬(升)值率。

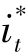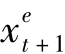由于很小，且也很小，故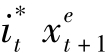会更小，故可以忽略(这一技巧在金融财务中常常使用，例如费雪方程式的i^·p被忽略，利率期限结构的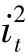被忽略)，则由式(9-9)可以得到我们要的“无抛补利率平价理论UIP”：

这即是汇率与利率在短期的关系。

为什么式(9-10)叫“无抛补”而不是“抛补”呢?让我们回到它的英文字：uncovered，这表示风险没有被“遮盖”(covered)。此乃因为在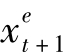内的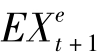是一个预期的观念，当投资者在t期对t+1期的汇率作预测，他面临的是一个不确定因素，汇率的变化也许会如他所预期，但也许会遽升或遽贬，令他有巨额损失，所以他仍有汇率上的风险，也因为如此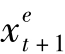，被称为“预期的”，而非实现的汇率利得或损失，故无抛补即风险没有被消除之意。

如何使用无抛补利率平价UIP(9-10)呢?让我们先练习运用这公式。这公式有一些陷阱，值得一提。

例9.1：如果为3个月美元利率，EX_t=30元为台币对美元汇率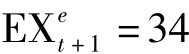，元为预期3个月后的汇率，则台币利率为多少?

错误的计算：

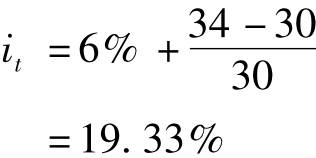
由于未考虑投资期间只有3个月，且利率已年息化，因而台币利率高估。正确的计算是先算出3个月的台币利率为：

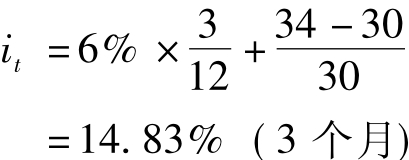
此式中，6%是3个月的“年利率”必须先转成3个月的利率(请参考第四章)，故要先乘以3/12。在此，3个月利率转成12个月的，可得59.32%。

下一个练习题值得一试。

练习题：

问：同上一练习题的数字，但i_t为已知(i_t=14.8%)，而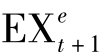为未知，请问台币的预期贬值率为多少?

答：错误答案：

先由公式算出

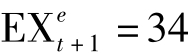
则台币预期贬值率为13.33%。

正确答案：

上述的答案是美元的升值率，而非台币的贬值率，正确算法应是先将台币视为“商品”，即EX改为1/EX，则台币预期贬值率为