研究成果介绍

1.2　研究成果介绍

在保险经济学的一般理论中，有一些重要理论，需要保险专业的研究生能够了解，这些重要的基本理论和基本观点是开启保险经济学研究工作的基本工具和基本技能。同时，了解保险经济学的国际国内学术前沿也是十分必要的，非常有利于研究生从中发现自己感兴趣的研究题目，以便在顺利查找到前人研究成果的基础上，完成一篇规范的学位论文，或者写出其他有价值的学术文章。很多“大牛”学者一生的创作精华就诞生在其读研阶段，而博士论文常常是其研究成果的顶峰。

博弈论、信息经济学和实验经济学、行为经济学的迅速发展是西方经济学发展的必然结果。为了使经济学看上去更科学，用推理严密但繁难深奥的数学模型来解释现实社会的经济行为成为经济学者若干年来所遵从的主流范式并已将之发挥到了极致，在这个过程中，西方经济学走过了一条漫长而曲折的道路。然而，人类的思想毕竟不同于天体的运行和物质的物理化学变化，人类的理性是不完全的，人的心理是瞬息万变的，也是要考虑风险考虑信息成本的，而风险和信息也是在时刻变化着的，于是经济学向更加关注人和人现实交易关系的方向发展，博弈论和信息经济学逐渐成为西方经济学的主流。这些还不够，随着生物化学和电子技术的发展，在实验室里分析人类经济行为的实验经济学和将心理学引入经济分析的行为经济学，更符合现实，也更能解释人们的经济行为。这些新的进展将经济学引入了一个更为正确的方向。

保险市场为经济学家开拓新的领域提供了一片广阔的天地，这里不但是信息极端不对称的场所，更是靠信息不对称的存在而存在的市场，如果没有信息不对称，投保人能够准确预知未来，保险的需求和供给都将化于无形。但一个信息过于不对称的保险市场却又是交易成本高企，道德风险和逆向选择难以控制的市场，在这样一个“夹缝”里，博弈论和信息经济学可以大有作为。

人们的保险需求决定于若干因素，风险状态、风险偏好、年龄结构、教育状况、家庭的性别结构、收入状况、收入结构、支出状况、支出结构、其他风险管理措施和其他生活保障措施的有无、家庭成员之间的关系、心理状态和对风险的感知和评价等等都对保险需求构成了或大或小的影响，是实验经济学和行为经济学成长的温床。

因此，当日内瓦大学的亨瑞·罗尔伯格（Henri Louberge）教授总结保险经济学发展历程的时候说：“令人惊奇的是，保险经济学的发展中很大一部分并不仅仅是保险经济学的发展，它们出现在一般经济学更广阔的领域：一方面保险经济学理论验证了一般经济理论；另一方面，保险经济学又促进了一般理论的发展。”

实际上，真的没有什么可惊奇的，就像湿润的草地会长出鲜嫩的蘑菇一样，保险市场的土壤中一定会生长出更艳丽的经济学奇葩。

下面就是几个保险经济学发展中的和心理学密切相关的理论命题。

1.2.1　期望效用理论的挑战与发展

世界科技发展的历史证明，科学的发展是建立在新理论对旧理论的挑战否定或者拓展的基础之上的，正如物理学从亚里士多德到牛顿再到爱因斯坦，科技的进步服从螺旋上升的规律。而在保险经济学中，到目前为止，风险理论的演变经历了三个阶段：从最早的布莱瑟·帕斯卡尔（Blaise Pascal）和皮尔·德·佛马特（Pierre de Fermat）17世纪提出的期望值理论（Expected Value Theory），到后来的冯·诺依曼和摩根斯坦恩提出的期望效用理论（Expected Utility Theory），再到丹尼尔·卡尼曼（Daniel Kahneman）^[14]和阿莫斯·特沃斯基（Amos Tversky）^[15]提出的前景理论（Prospect Theory）。这三个阶段的飞跃式发展都是在对前人理论的挑战中实现的。

冯·诺依曼和摩根斯坦恩的期望效用函数因为解决了贝努利的圣·彼得堡悖论（St.Petersburg Paradox），而取代了占据了几百年统治地位的期望值理论；而最早对期望效用理论提出挑战则来自阿拉斯悖论（Allais Paradox）。

作为一种个人行为理论，期望效用模型具有许多标准消费理论的基本假设。比如要假设选择的对象（即商品束、保险产品或者彩票）能够清楚而客观地界定，这意味着相同的可行集（例如相同的预算约束集、相同的市场环境集）将导致相同的选择结果。在每种情形下，还要假设个人能够做一些必要的数学运算来决定可行集，例如在不同的集合中加总数量，或者计算复合概率或条件概率。最后还要假定在每一个例子中个人偏好都具有传递性（也译为递移性），也就是说，如果个人较之第二个选择对象（选择对象可以是商品束或风险收益，如投资、彩票和保险）更偏好第一个选择对象，同时较之第三个选择对象更偏好第二个选择对象，那么他或她较之第三个选择对象会更偏好第一个选择对象。^[16]那么，这些假设在理论和现实中成立吗？

期望效用函数中最重要的内涵来自于期望效用最大化或偏好函数∑U（x_i）p_i的形式。尽管该偏好函数放弃了期望值规律的形式∑x_ip_i，它仍然保留了该形式的其他关键性质，特别是线性概率的特征。马克·马金纳曾用图形这种最直观、最简单的方法解释了什么是线性概率，并用图示说明，这样的假设在一定程度上会脱离现实。

假设三种彩票的奖金分别为：

x₁＜x₂＜x₃

三种彩票中奖的三维概率集合为：

P＝（p₁，p₂，p₃），其中p_i＝prob（x_i），∑p_i＝1

因为p₂＝1－p₁－p₃，所以我们能够用在（p₁，p₃）平面中的单位三角形（图1－2）来表示这些彩票。在三角形中，向上运动将增加p₃同时减少p₂（即使得收益x₃的概率变大，收益x₂的概率减小），向左移动将减少p₁增加p₂（即使得收益x₂的概率变大，收益x₁的概率减小）。这些移动（更一般地说，所有向左上角的移动）都会产生随机占优彩票。

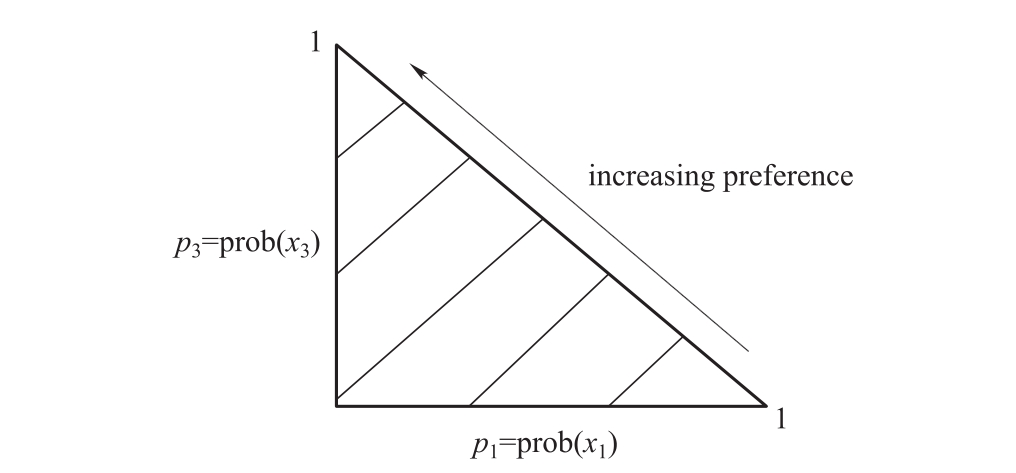
图1-2　单位三角形中的期望效用无差异曲线

所谓的随机占优是指：对于两种彩票，在收益相同时，其中一个获得收益的概率更高，或在获得收益的概率相同时，其中一个获得的收益更高，或者其中一个彩票比另一个彩票具有更高的收益且具有更高的获得对应收益的概率，那么就可以说该彩票随机占优另一彩票，比如，以2 ／3：1 ／3的概率获得＄100或＄20和1 ／2：1 ／2的概率获得＄100或＄30都随机占优于1 ／2：1 ／2的概率获得＄100或＄20。

在（p₁，p₃）图中的个人的无差异曲线可以通过下面线性方程的解得出：

无差异曲线由斜率为u（x₂）－u（x₁[]）／ u（x₃）－u（x₂[]）相互平行的斜线构成，更高的无差异曲线位于左上方。这意味着想要知道在整个三角形上一个期望效用最大化个人的偏好，只要知道一条无差异曲线的斜率就够了。

为了理解如何使用该图形来解释风险态度，观察图1－3和图1－4。图中的实线是期望效用的无差异曲线；虚线是等期望值线。

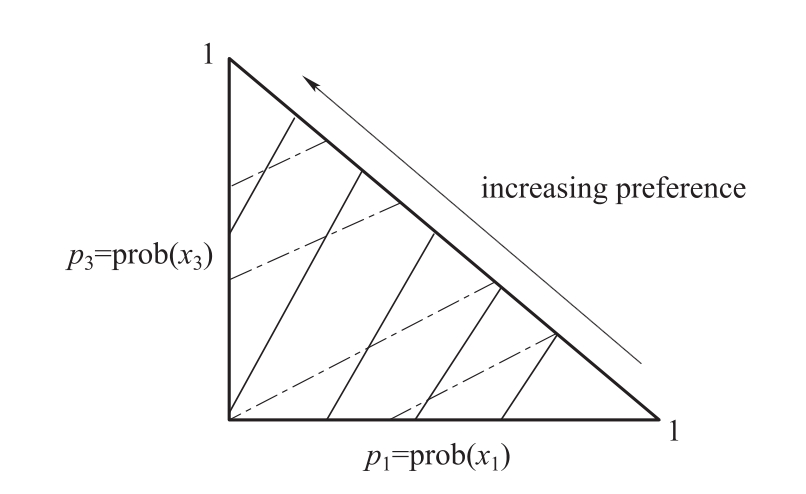
图1-3　风险厌恶者相对陡峭的期望效用无差异曲线

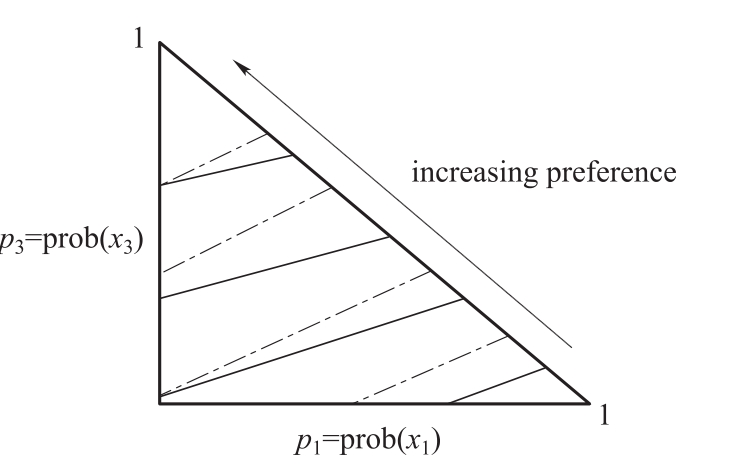
图1-4　风险爱好者相对平缓的期望效用无差异曲线

等期望值线是下面方程的解：

因为沿着这些直线向右上方向移动不会改变回报的期望值，但会增加出现小概率事件x₁和x₃的概率，减少出现概率较大的事件x₂的概率。如图1－3所示，风险厌恶型的期望效用函数U（· ）是凹形的，所以其无差异曲线比等期望值线更陡峭。无差异曲线的斜率是：

而等期望值线的斜率是：

当x₁＜x₂＜x₃时，凹的效用函数U（·）意味着：

因此风险的增加将导致较低的无差异曲线。风险偏好型效用函数U（· ）是凸型的，风险的增加对应较高的无差异曲线。如果我们比较两种不同的效用函数，其中一个的效用函数比另一个的效用函数更加厌恶风险，那么该效用函数将具有更加陡峭的无差异曲线。

在行为上，我们可以把概率的线性特性作为个人对复合彩票概率偏好的一种限制条件。如果p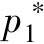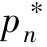^*＝，…，）和p＝（p₁，…，p_n）是两个彩票，其概率对应的回报集合为（x₁，…，x_n）。

则以α：（1－α）构成的复合概率是：

我们可以认为该回报｛ x₁，…，x_n｝所对应的概率和α的概率获得p^*和（1－α）的概率获得p的两阶段彩票的概率相同。因为概率的线性特性意味着：

期望效用最大化个人将表现出如下特征：如果对两个彩票p^*和p，个人更偏好彩票p^*（或对两彩票无差异），那么对两个复合彩票αp^*＋（1－α）p^**和αp＋（1－α）p^**，个人更偏好彩票αp^*＋（1－α）p^**（或对两彩票无差异）。这就是萨缪尔森（Samuelson）1952年提出的众所周知的独立性公理。

以上性质实际上就是概率的线性特性，该性质可以解释如下：就回报{x₁，…，x_n}所对应的最终概率而言，在两个复合彩票αp^*＋（1－α）p^**和αp＋（1－α）p^**之间选择如同投一枚硬币，问当出现正面时，你愿意要彩票p^*还是p，已知当出现反面时，你将获得彩票p^**，出现反面的概率是（1－α），出现正面的概率是α。现在每枚硬币都有可能出现反面，但此时你的选择就并不重要了，因为你总得到彩票p^**，但如果出现正面的话，你的选择最终落到p^*和p上，如果你是理性的，你将做出和上面相同的选择。

以上所论述的观点是描述性的，但是经济学家把期望效用作为不确定下选择理论中的一种描述性的理论，所以在这方面上述观点起到了关键的作用。随着反对该模型的证据不断增多，两种观点之间的冲突也日益激烈，一种观点是把经济分析作为一种他们所认为的理性行为的描述和预测，另一种观点是把经济分析作为一种可观测行为的描述和预测。

阿拉斯悖论就是在这种情形下被提出来，构成了对期望效用理论的假设线性概率的挑战。

要求人们在下面的两组赌博中选出每组中所偏好的选择对象：

定义{x₁，x₂，x₃}＝{＄0；＄1 000 000；＄5 000 000} ，如图1－5和图1－6所示，在（p₁，p₃）三角形中这四个赌博可以看做一个平行四边形。在期望效用假设下，在第一对赌博中，偏好赌博a₁意味着个人的无差异曲线相对来说较陡峭，其形状如图1－5所示；同样，在第二对赌博中，偏好赌博a₄意味着个人的无差异曲线相对来说较陡峭，其形状如图1－6所示。在另一种无差异曲线较平坦的情况下，个人将偏好赌博a₂和a₃。然而，像阿拉斯（1953），毛瑞森（Morrison）（1967），拉法（Raiffa）（1968），索维克（Solvic）和特沃斯基（Tversky）（1974）这些学者都发现大部分的选择结果是个人在第一对赌博中选a₁，而在第二对赌博中选a₃，这意味着无差异曲线不是平行的，而是扇状分布的，形状如图1－6所示。

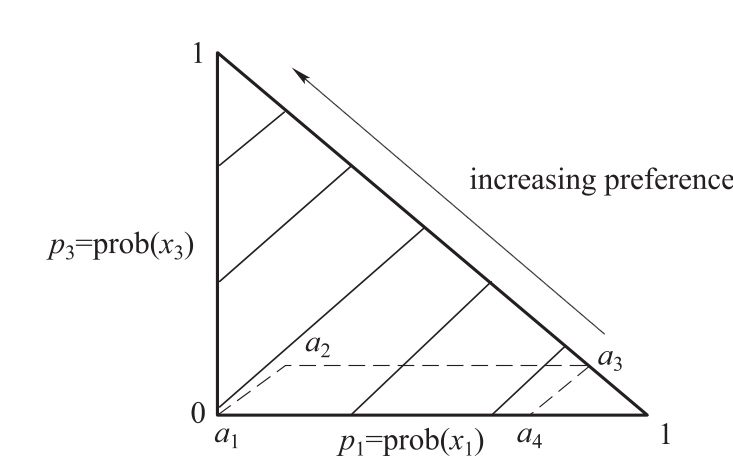
图1-5　期望效用的无差异曲线和阿拉斯悖论

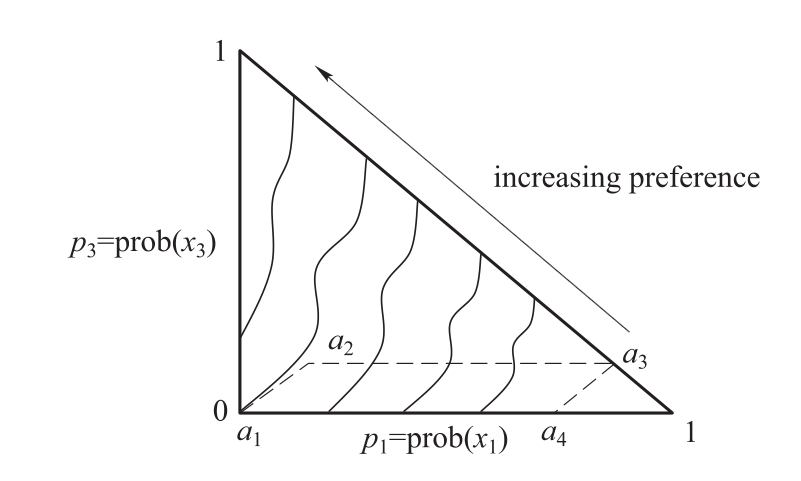
图1-6　期望效用无差异曲线的扇形分布和阿拉斯悖论

以上的分析给出了一个显而易见的结果，期望效用函数中概率分布的线性假设并不完全正确。有意思的是，经济学家们看到这个结果之后，其反应却令人哭笑不得：难道我的选择错了吗，我的选择违背了独立性公理吗？

经济学家萨维奇（Savage）的反应具有代表性，他最初的选择也是a₁和a₃。然而萨维奇毕竟是饱经经济学训练的“理性人”，他经过思考下了个结论说：我刚才选择a₁ 和a₃是错误的。是不是有点像皇帝最宠信的那个老大臣，见到骗子们在织布机上忙碌的反应首先是吃惊，我真的是一个愚蠢的或者不称职的人吗？接来下的反应就是思考一会儿，说：皇帝的新装真美丽。

后来众多学者的研究结果证明，个人的偏好的无差异曲线服从扇形分布，各种有关偏好的非期望效用被设计出来并在研究中得以广泛应用，特别是周恕弘（Chew Soo Hong）^[17]和费什波恩（Peter Fishburn）先后提出来的非期望效用模型：

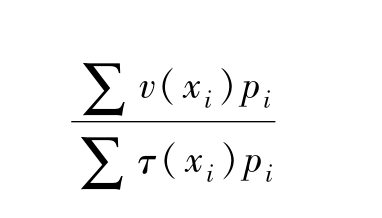
奎金（John Quiggin）1982年提出来的非期望效用模型：

∑v（x_i）［g（p₁＋…p_i）－g（p₁＋…＋p_i－1）］

以及马金纳1982年提出来的非期望效用模型：

∑v（x_i）p_i＋［∑τ（x_i）p_i］²

这些非期望效用模型^[18]表现出了随机占优偏好，风险厌恶或爱好的扇形分布的特性，在理论上和实践中具有很好的应用价值。

需要格外注意的是，非期望效用模型并没有放弃期望效用理论框架内所形成的大量理论结果，特别是期望效用模型对保险最优决策研究仍然很有用处，对于规范地分析不确定情况下经济行为以及在保险等许多领域的衍生应用，标准线性期望效用模型一直是标准范例，因为非期望效用偏好分析并不是仅仅采用特定的非线性函数，而是综合考虑非线性函数，用微积分来拓展期望效用理论中的结果，采用的方式和拓展线性函数下的结果相同。所以期望效用理论在分析中仍然有用。

1.2.2　框架效应

框架效应（Framing Effects），也被直译作“结构效应”，或者意译为“语境效应”，是说替代性的表现方法的不同，或概率相等的选择项之上表述问题的“框架”不同，或者说同一问题的语境不同，将会导致选择上的系统性差异。

著名的“亚洲疾病问题实验”是对框架效应较直白的解读。1981年丹尼尔·卡尼曼、保尔·索罗温克（Paul Slovis）和特沃斯基在剑桥大学出版社出版的《不确定情形下的判断：启发性和偏差》（Judgement Under Uncertainty：Heuristic and Biases）给出了一个影响深远的实验结果：

想象美国正讨论如何对付一种罕见的从亚洲传来的疾病，预计该疾病的发作将导致600人死亡。现有两种应对这种疾病的方案可供选择。假定对两个方案实施效果的精确科学估算如下所示：

情景一：对第一组参加实验的152人叙述下面情景：

如果采用A方案，200人将获救。

如果采用B方案，有1／3的概率600人将获救，而有2／3的概率无人将获救。

结果是：在被测试的152人中，72%的人选择了方案A，28%的人选择了方案B。

情景二：对第二组参加实验的155人叙述同样的情景，同时将解决方案改为C 和D：

如果采用C方案，400人将死去。

如果采用D方案，有1／3的概率将无人会死去，而有2／3的概率600人将死去。

结果是：在被测试的155人中，22%的人选择了方案C，78%的人选择了方案D。

实质上，情景一中的方案A和情境二中的方案C，情景一中的方案B和情境二中的方案D是完全一样的，但描述方式或者说语境的改变使得人们认识事物的参照点^[19]发生了变化，选择的结果发生了决定性逆转。

为什么会这样？行为经济学家和心理学家给出的答案是：情景一描述的结果是收益———生还；而情景二描述的结果是损失———死亡。用获救来“说话”时，人们的感觉大概是：生命是宝贵的，能救多少是多少，因此多数人会因风险厌恶而选择A方案；反之，当用死亡来“说话”描述同样的事件时，人们会觉得这样的损失难以接受，人们不希望眼睁睁地看着400人牺牲，这时人们会偏好，受赌一把是多数人的心理。

可见，不同的语境下，人们对待风险的态度是不同的。面临收益时人们会小心翼翼选择风险规避；面临损失时人们甘愿冒险，呈现的是风险偏好的倾向。

更早一些，卡尼曼和特沃斯基在1979发表在《计量经济学》（Econometrica）上的文章《前景理论：风险状态下的决策分析》（An Analysis of Decision Under Risk）给出了一个数字化的经典案例：

除了你所拥有一切外，还给你1 000以色列镑，要求你在确定能获得500镑和1／2概率获得1 000镑1／2的概率获得0镑中作出选择；

除了你所拥有一切外，还给你2 000以色列镑，要求你在确定损失500镑和1／2概率损失1 000镑1／2的概率损失0镑中作出选择。

这两个问题的最终财富具有同样的分布。然而，把这两个问题分别放到两组调查对象中进行调查时，对于第一个问题有84%的被调查对象选择确定性收益，而对第二个问题则有69%的人选择上述的1／2概率损失1 000镑，1／2的概率损失0，而没有选择确定损失500镑。

其他学者的相关研究中也显示了大致相同的结果，如斯扣梅克（Schoemarker）和昆如路塞（Kunreuther）1979年的研究结果，麦克内尔（MacNeil），保克（Pauker），索克斯（Sox）和特沃斯基（Tversky）1982年的研究结果，李森斯坦（Lichtenstein）1982年的研究结果都说明了框架效应的存在。经过若干年的讨论，不管是在实验室中，还是在现实生活中，框架效应广泛性和可重复性已经变得无可争议了。

而在保险市场上，框架效应的例子也是不胜枚举。比如，A保险公司规定，某健康保险的被保险人如果在60岁以下，则可以享受10%的费率优惠；而同样的一份健康保险保单，B保险公司则规定，如果被保险人的年龄超过60岁，则要多收取10%的费率。应该说这两个保险公司的规定并没有实质的差别，但对投保人的吸引力却有相当大的不同。投保人对“赚”10%和亏10%的态度显然是不同。

当衡量一个交易时，人们对于“损失”的重视要比同等的“收益”大得多。因此，企业在进行价格定价或促销时，应该将顾客的选择与“收益”而不是“损失”联系在一起，从而有效激励消费者的购买行为。

框架效应的存在再一次确认了保险制度的价值，保险就是要将你失去的东西还给你，让你不至于因失去某件东西而效用大减或者太过悲伤，尽管保险的补偿仅仅还局限于物质补偿层面。

1.2.3　前景理论

与框架效应相比，前景理论则更加系统，且经过诸多学者若干年的优化，目前已经是一个比较系统的理论体系。前景理论最早是由丹尼尔·卡尼曼和阿莫斯·特沃斯基于1979年提出来的。

1.2.3.1　前景理论的简要概括

概括而言，前景理论由几个基本原理组成，分别是确定效应（Certainty Effect）、反射效应（Reflection Effect）、损失规避（Loss Aversion）、孤立效应（Isolation Effect）和锚定效应（Anchoring Effect）。

1.确定效应：在确定的收益和“赌一把”之间，做一个抉择，多数人会选择确定的好处，和确定性的结果相比个人会低估概率性结果，也就是说大多数人在面临收益的时候是风险厌恶的。

最常见的例证是在股票市场上。实证数据显示，投资者持有亏钱股票的时间要远远长于持有赚钱股票的时间，见好就收和落袋为安的大众选择与“对则持，错即改”的投资核心理念背道而驰。

2.反射效应：在确定的损失和“赌一把”之间，做一个抉择，多数人会选择“赌一把”，也就是说，大多数人在面临损失的时候是风险爱好的。最常见的实验是，让参加实验的人从下面两个选项中作出选择：

A.确定会赔30 000元；

B.有80%的概率可能赔40 000元，20%的概率不赔钱。

显然：（－40 000）× 80%＋0 × 20%＝－32 000＞－30 000元。经过简单计算，多数人应该选择A，但实验的结果是多数的人选择了B。在忍受确定的损失和“与命运抗争”之间，多数人选择了后者，这就是反射效应。

3.损失规避：多数人对损失比对收益更为敏感。同样的金额在得到与失去之间，对应着大小不同的效用，捡到100美元的快乐小于失去100美元的痛苦。

萨勒（Richard Thaler）教授^[20]提供的案例是对“损失规避”最贴切最通俗的解释：假设你得了一种病，有万分之一的可能性（低于美国年均车祸的死亡率）会突然死亡，现在有一种药吃了以后可以把死亡的可能性降到零，那么你愿意花多少钱来买这种药呢？那么现在请你再想一下，假定你身体很健康，如果说现在医药公司想找一些人测试他们新研制的一种药品，这种药服用后会使你有万分之一的可能性突然死亡，那么你要求医药公司花多少钱来补偿你呢？在实验中，很多人会说愿意出几百块钱来买药，但是即使医药公司花几万块钱，他们也不愿参加试药实验。

这其实就是损失规避心理在作怪：得病后治好病是一种相对不敏感的收益，而本身健康的情况下增加死亡的概率对人们来说却是难以接受的损失，显然，人们对损失要求的补偿，要远远高于他们愿意为治病所支付的钱。

芝加哥大学商学院教授奚恺元（Christopher k.Hsee）^[21]关于餐具实验的案例也同样经典：家具店正甩卖餐具，有一套餐具，有8个菜碟、8个汤碗和8个点心碟，共24件，每件都是完好无损的；而另外一套餐具有40件，其中24件和刚刚提到的完全相同，而且完好无损，另外这套餐具中还有8个杯子和8个茶托，其中2个杯子和7个茶托都已经破损了。顾客在只知道其中一套餐具的情况下，实验观察的结果是：人们愿意为第一套餐具支付33美元，却只愿意为第二套餐具支付24美元。

第二套餐具比第一套多出了6个好的杯子和1个好的茶托，人们愿意支付的钱反而少了。这是因为24件和31件餐具到底是多还是少，如果不互相比较是很难引起注意的，但是整套餐具到底完好无缺还是已经破损，却是很容易判断的。餐具的破损意味着损失，规避损失是人们经济活动的心理基础。

商业活动中，商家经常会利用人们的“损失规避”心理推销自己的产品，比如某名牌卫浴厂商在推销可冲洗烘干的马桶时就给客户提供了90天的试用期，90天内喜欢再付费，不喜欢可原物退还厂家，结果退货率极低，商品销售取得的巨大的成功。人们在用了这么好的东西后已经产生了依赖，由奢入俭，将极大地降低客户的效用。

也有学者将这一类的效应拿出来称为“禀赋效应”（Endowment effect）、“幼犬效应”（Puppies effect）^[22]、“所有权依赖症”，但说的都是已经拥有的东西失去时，其痛苦会成倍放大。

保险公司利用客户的损失规避心理那就更是家常便饭了。因为从原理上，保险就是把被保险人失去的东西还回来，不至于让人们那么痛苦。而保险公司到处赠送的保额较高保费低廉的意外伤害保险，都是生动的案例。

4.孤立效应（Isolation Effect）：孤立效应最早起源于对主观概率的研究。经济学家给出的案例一般都会设定一个先验的概率，人们根据事件发生概率作出选择，然而，大量的证据表明，在现实中，所谓的客观概率并不为人们所知，人们作出判断和选择常常是根据个人的“主观概率”，由此偏离贝叶斯概率的选择成为一种常态。

有一句话很经典：买彩票是赌自己会走运，买保险是赌自己会倒霉。这是两种“小概率”事件，但人们却十分热衷。为什么呢？原因在于小概率事件所具有的震撼力使人们在做经济决策时将那些“大概率”事件潜意识地屏蔽掉了，卡尼曼与特沃斯基称之为“小数法则”，即人们通常会根据自己已知的印象深刻的少数例子来做推测。彩票中500万元大奖的新闻经常会成为人们茶余饭后的谈资，令人恐怖的自然灾害和意外事故总是触目惊心，而保险的赔付案例和赔付数额也会经常被保险公司大肆渲染。潜移默化下，在人们的头脑中，小概率事件的印象非常深刻，当人们做经济决策时，想到的大多是已经发生的小概率事件，因此人们花钱买彩票的时候大脑里常常会浮现出中大奖之后的未来。人类强调小概率事件的倾向称为“孤立效应”。

彩票盈利的概率非常之低，但彩票的销售量却异常的大，2010年中国体育彩票销售额达到700亿元，而2011年前11个月，中国福利彩票的销售量就达到1 000亿元，2010年中国保险市场的保费收入是1.47万亿元。

保险已经深入到社会生活的各个层面，虽然发生合同约定的自然灾害和意外事故的概率非常低，但孤立效应还是促使人们尽可能转嫁这些风险。显然，孤立效应是保险公司经营下去的心理学基础。

在小概率事件面前人类对风险的态度是矛盾的，人们一手买保险，一手买彩票，同一个人既是风险喜好者，又是风险厌恶者，传统经济学无法解释这个现象。行为经济学的解释是：彩票和保险是两个分立的“心理账户”，面对小概率的赢利，人们大多表现出风险爱好者的特征；而面对小概率的损失，人们大多表现出风险厌恶者的特征。

5.锚定效应：也称为“参照依赖”，是指当人们需要对某个事件做定量估测时，会将某些特定数值作为起始值，也就是参照点，参照点像锚一样制约着估测值，人们对得失的判断并作出的选择往往由参照点决定，也就是说在做决策的时候，会不自觉地给予最初获得的信息过多的重视。估计出来的损失和获得是相对于参照点而言的，改变人们在评价事物的观点，也就可以改变人们对风险的态度。

研究人员请两组高中生在5秒之内估计8个数字连乘之积大概是多少。

第一组学生看到的是：

1×2×3×4×5×6×7×8＝？

第二组学生看到的是：

8×7×6×5×4×3×2×1＝？

正确答案是40 320。因为时间太短，所有的学生因为时间限制来不及乘完所有的数得出正确答案，多数人的做法是先把几个数乘出来，作为“锚点”，然后估计最终答案。因为“锚点”不同，估值结果相去会甚远，而最终统计完全符合研究人员预测的结果：第一小组的平均估值为512；而第二小组的平均估值为2 250。这就是锚定效应的经典实例。

一个人住在城区三室一厅的房子里是不是一定感觉到很幸福呢？这要看他作出判断的锚点在哪了，如果原来他住的平房，比较起来他当然会觉得幸福，但如果他原来住的是豪华别墅，那他感觉到的可能更多的是失落。如果他的锚点是在其他人那里，原来和他一起住平房的邻居都住进了豪华别墅，而他住在三室一厅的房子里，他的心理也未必是“溢满了幸福”。

锚定效应在商业中常被应用：美国纽约的第五大道是纽约曼哈顿区的中央大街，是全球排名第一租金最昂贵的商业街，道路两旁是玻璃幕墙闪闪发亮的高楼大厦，这里也汇聚着施华洛世奇、LV、维多利亚的秘密等世界最著名的珠宝、皮件、服装、化妆品名牌的旗舰店和专卖店。此处也是好莱坞巨星、各国的达官富豪、社交名媛们最喜爱的购物场所，我们普通老百姓在这里看一遍，再回到自己居住的小区，发现所有东西都是便宜的，尤其是那些名牌产品，购物欲望可能就会被激发出来，因为我们已经被第五大道的高价格所“锚定”。

在第五大道的专柜里，我们会看到价格高到匪夷所思的商品，24万美元的包，16万美元的镶钻内衣，72万美元的手表，11.2万美元的黄金绒毛泰迪熊，96万美元的钻石笔记本电脑。实际这些产品并非是真正地想出售出去，它的标价无非就是个锚定，这个价格让你确定它就是顶级品牌，买同一品牌的什么价位的其他东西都不再觉得贵，反而觉得是个大便宜。

实践价值在那里，所以对锚定效应研究者众，成果众多，经济学家们给出众多类别的锚定效应，如语意锚定也称标准锚定（Standard Anchoring）、数字锚定（Numerical Anchoring）、潜意识锚定（Subliminal Anchoring）、自生锚定（Self-generated Anchoring）与实验者锚定（Experimenter-provided Anchoring）等等。

中国保险的营销人员经常跟客户讲的一句话是“拿出你年收入的10%买保险是合适的”。这句话就是对锚定效应在保险业的具体应用，就像金店的店员常给顾客的标准答案：买一个订婚钻戒至少应是你“两个月的收入”。这种标准的荒谬性在于它只强调影响顾客消费的一个因素而彻底忽略其他，而一个家庭或者个人应该拿出多少钱买保险是由风险状态、风险态度、收入结构、支出结构、家庭结构等十几个指标共同决定的，而不仅仅决定于顾客的收入，但一旦被保险公司这种标准所锚定，客户就可能会把更多的钱浪费在不合适的保险产品上。

目前对锚定效用的研究主要集中在以下几个方面：对锚的种类和结构的研究、锚定效应研究范式的创新、对锚定效应的神经心理机制的研究、对锚定效应影响因素的研究、对锚定现象对人的心理与行为的正负面影响的研究、对锚定效应与其他有关心理现象之间关系的研究。

1.2.3.2　前景理论在保险市场中的应用

整个前景理论在保险业中的应用随处可见。比如中国人寿保险分公司给某营销服务部确定月度保费任务。此时营销服务部有两种选择：

营销方案A：保费收入2 000万元，100%能完成；营销方案B：50%的概率可获得保费收入3 000万元，50%的概率可获得保费收入1 000万元。

如果分公司的保费收入目标定得比较低，比方说是1 000万元，那么方案A看起来可以稳稳地多收入保费1 000万元，已经超额完成任务，可以获得一定的奖励；而方案B则是要么刚好达到目标，要么多盈利2 000万。A和B看起来都是收益，这时候营销服务部的大多数员工可能不愿冒风险，倾向于选择方案A。

而反之，如果公司的目标定得比较高，比如说3 000万，那么采用方案A显然会确定少收入1 000万元的保险费，没有奖励还会有惩罚；而B方案则要么刚好达到目标，要么少获得2 000万保费收入，这时候两个方案都是损失，多数员工此时会抱着冒冒风险说不定可以达到目标的心理，选择有风险的投资方案B。

鼓励员工稳健，还是冒险，营销服务部行动方向的“扳机”就掌控在分公司制定保费收入计划部门的指尖上。

另一个例子则说明保险这种商业机制有着由政府部门配置资源所达不到的效率和效果：浙江台州是个风灾比较严重的地方。某年月日，台州的某个镇不幸遭到了强台风的袭击。假如这个镇上有1 000户居民，90%居民的房屋都被台风摧毁了，那么政府需要救助多少钱才能基本达到老百姓的满意呢？但假如这个镇上有10 000户居民，其中有20%居民的房子被摧毁了，政府部门又该救助多少钱才能基本达到老百姓的满意呢？

从客观的角度来讲，后面一种情况下的损失显然更大。可实验的结果显示，人们觉得在前面一种情况下，政府至少需要支援4 000万元，但在后面一种情况下，人们觉得政府只需要支援1 000万元就已经足够了。据说，这个最初以联合国救灾为蓝本的行为经济学实验的结果是：从一般的市民到政府官员，对这样的安排，都几乎是同样的态度。

反过来，如果不是政府救灾，而是利用商业保险进行保障和补偿，这个问题就比较简单了，保险公司只需要及时合理地查勘定损，然后按照保险金额和保险合同条款来赔付就是了，也不需要政府动那么多的脑筋，来决定需要救助多少钱，财政预算怎么安排、资金怎么样分配才公平，如何监督才能减少救灾中的渗漏和腐败等等。

从微观角度，保险营销中的话术很多就是利用了投保人心理上的孤立效应和锚定效应，而话术的滥用从长期来看，实际上对保险业的声誉和长远是非常不利的。从政府的宏观决策层面，长期养老保险和长期护理保险这种社保功能替代型比较强的险种应该像发达国家一样，及早出台免税和延税政策，利用保险制度广泛提高公民的效用水平，维护社会稳定，缓解贫富分化而带来的心理落差。

1.2.4　扶摇直上的宏观经济学

传统经济学崇尚的是基于精密数学模型的理性主义，而心理学则强调实验，认为人的理性是有限的。实验经济学和行为经济学的进展使微观经济学的研究指向的不再单纯是金钱和数字，而是如何最大化公民的幸福感，这和保险市场的存在价值和发展目标殊途同归。微观经济学的发展为保险市场的分析提供了新的思路和方法。

另一方面，美国次贷危机引发的金融危机特别是后来的欧债危机和欧元危机则使原来不成体系颇受冷落的宏观经济学得到了高度重视。2011年10月10日，瑞典皇家科学院公布2011年诺贝尔经济学奖授予普林斯顿大学的克里斯托弗·西姆斯（Christopher Sims）以及纽约大学的托马斯·萨金特（Thomas J.Sargent）。

西姆斯在时间序列计量经济学和应用宏观经济学领域中是一位非常有影响的经济学家。瑞典皇家科学院发表声明说，西姆斯研究出了一套基于VAR模型的方法，以研究短期的政策调整，比如利率调整如何影响实体经济，两位学者解释了是什么让世界经济形势至此，下一步全球宏观经济可能发生的变化，政策将作何改变。

萨金特是理性预期学派的领袖人物，对政府政策效果的研究有着广泛而深远的影响。萨金特认为：对任何一项政策，理性经济人都会调整自己的博弈策略，即所谓的“上有政策，下有对策”，人们理性地应对政策并作出调整的结果是使政策失效，所以其研究成果的一个核心思想是政府最佳政策是少出政策，实现无为而治。

经济危机之后，一些国家和地区的政府部门借机加强对资源、市场和权力的控制，2011年的颁奖实际上也是经济学界对这种倾向的提醒。以此来对照中国的保险市场，监管部门对市场的控制力量在逐渐增强，监管部门“引领保险市场发展”的思路已经引起人们的反思。

2010年的诺贝尔经济学奖则颁发给了研究劳动力市场的美国经济学家彼得·戴蒙德（Peter A.Diamond）、戴尔·莫特森（Dale T.Mortensen）和英裔、塞浦路斯籍经济学家克里斯托弗·皮萨里德斯（Christopher A.Pissarides）。戴蒙德是世代交叠模型的提出者，社会保障、养老金和税收问题专家。莫特森的研究领域集中在劳动经济学、宏观经济学和经济理论，尤其是在工作搜寻和失业理论方面颇有造诣，并且将其扩展于劳动调整、研发、个人关联以及劳动再分配等方面的研究。

2009年诺贝尔经济学奖由制度经济学的代表人物美国印第安纳州大学政治学教授艾利诺·奥斯特姆（Elinor Ostrom）和加州大学伯克利分校经济学家奥利弗·威廉姆森（Oliver E.Williamson）。奥斯特姆在公共选择方面的研究和威廉姆森在制度经济学的研究促使经济管理从经济学边缘研究成为前沿研究课题。

2008年诺贝尔经济学奖得主是国际贸易理论方面的保罗·克鲁格曼（Paul R.Krugman）；2007年诺贝尔经济学奖得主是研究机制设计理论的莱昂尼德·赫维奇（Leonid Hurwicz）、埃里克－马斯金（Eric S.Maskin）以及罗杰·迈尔森（Roger B.Myerson）；2006年的诺贝尔经济学奖颁发给了现代宏观经济学的缔造者埃德蒙·费尔普斯（Edmund Phelps）；2005年的获奖者制度研究博弈论的罗伯特·奥曼（Robert J.Aumann）和托玛斯·谢林（ThomasC.Schelling）；2004年诺贝尔经济学奖给了动态宏观经济学领域的挪威经济学家芬恩·基德兰德（Finn Kydland）和美国经济家爱德华·普雷斯科特（Edward Prescott）。

从经济学的主流发展倾向来看，宏观经济学引起了人们越来越多的研究兴趣。不少经济学家预测，在全球经济没有彻底摆脱困境之前，宏观经济学热度会与日俱增。因为很明显的是，当今世界，某些金融集团控制了金融市场，然后通过金融市场控制了某些国家、地区和乃至整个世界的经济命脉。人们发现成千上万人辛辛苦苦兢兢业业的劳动成果被一些金融大鳄在极短的时间内就可以洗劫一空。亚洲金融危机、日本经济衰退、美国次贷危机，新兴国家几十年的资源损耗环境破坏和对劳动力的剥削所换回来的竟然是那些发达国家永远也偿还不了的债券和日渐贬值的货币，在一些金融机构的操作下，一些国家的经济顷刻之间就可以濒于崩溃，这些无疑都是宏观经济和世界经济的问题。是谁在用现在的国际经济制度掠夺财富，国民的财富保卫战该如何打，这些都是经济学界需要回答的问题。

商业保险作为现代市场经济和金融体系的重要组成部分，并通过国际再保险体系将整个世界的风险链接在一起，一旦一个国家或地区巨型的自然灾害和意外事故发生（比如数倍于美国“9·11”的灾难），将对整个世界的经济安全构成威胁，所以无论是作为一个产业，还是宏观经济学中对风险和保险市场的分析，保险经济学都从未缺席。