静止人口与稳定人口

4.2　静止人口与稳定人口

这一节将考察人口描述模型的两种重要的特殊情形。

4.2.1　静止人口模型

当l（x，u）与u无关时，相应的模型称为静止人口模型。此时

其中b是常数出生密度，s（x）是不依赖于出生时间的生存函数。

可以将（4.8）改写为

这里b等同于l₀。

对于静止人口，（4.5）成为

即静止人口在时间t₀介于年龄x₀与x₁之间的人数可用函数T_x表示。

Tx表示初始l₀个成员的生存组在年龄x以后生存总年数的期望值。

由图4.4给出的l_xμ_x解释可以得到

可作为在年龄x₀与x₁之间的死亡在任何时间t的密度。

以上这些特征可以清楚表明静止人口这一概念。

4.2.2　稳定人口模型

当人口密度函数具有以下形式：时，相应的模型称为稳定人口模型，这里b＞0及R是常数，s（x）是不依赖于出生时间的生存函数。如R＝0，则稳定人口成为静止人口。在稳定人口中，在时间u的出生密度为e^Rub＝e^Rul₀。

稳定人口在时间t的总人口为

由此可见，当R＞0时人口呈指数式增长，而当R＜0时人口呈指数式递减。

稳定人口中在时间t时介于年龄x₀与x₁之间的人数占总人口的比例为

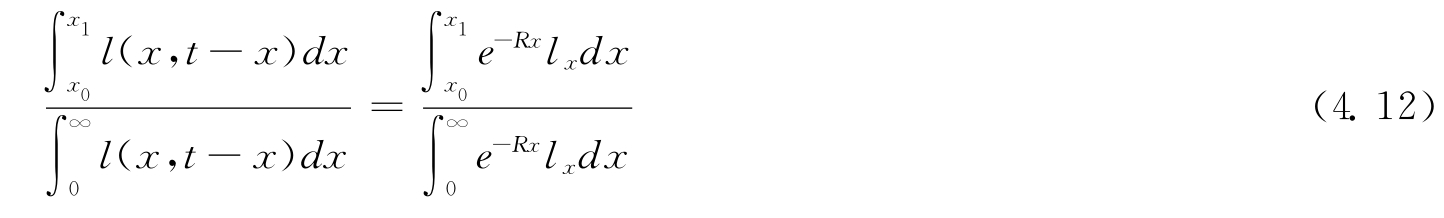
与时间t无关。因此，尽管稳定人口的总规模可随时间改变，但相对的年龄分布保持不变。

稳定人口在时间t时介于x₀与x₁岁之间的人数可用计算基数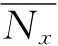来表示：

这里及以下记号中的一撇表示计算时使用的利息效力等于稳定人口的（瞬时）变化率R。

根据（4.7），稳定人口的死亡效力为：

它与出生时间无关。年龄介于x₀与x₁之间的人在时间t的死亡密度为：

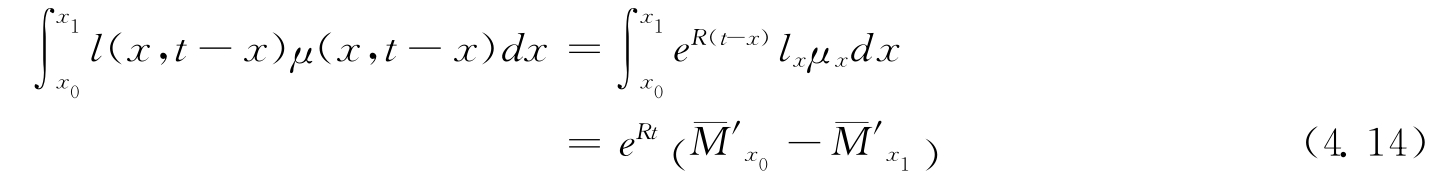
4.2.3　新出生人口模型

在建立出生函数的数学模型过程中，需要引入生育力函数，记为β（x，u）。β（x，t－x）dt表示x岁妇女在时间t与t＋dt之间生育的女孩数，x岁妇女自己是在时间t－x出生的。生育力函数是各年龄及各代妇女生育的女婴瞬时出生率。

在时间t与t＋dt之间出生的女孩总数为：

在（4.15）中的下标f表示有关函数与女性生命相联系。总的出生数（包括男孩）可通过乘一个常数获得，该常数为女孩出生数与总出生数之比，在大多数人口中稍稍比2大些。

在（4.15）两端除以dt，并以（4.1）取代l_f（x，t－x），我们可看出女性出生密度函数满足积分方程

在已知函数s_f（x，t－x）与β（x，t－x）时求解b_f（t）。在（4.16）中，乘积函数s_f（x，t－x）β（x，t－x）称为净孕产函数，记为φ（x，t－x）。

我们假定净孕产妇函数不依赖于母亲的出生年代，即s_f（x，t－x）β（x，t－x）＝φ（x），则积分方程（4.16）成为

在考虑b_f（t）＝be^Rt的特殊情况下，代入方程（4.17）得：

通过方程（4.18）可以求得R。