【摘要】：飞行器的姿态运动学方程有多种描述形式，常用的有采用欧拉角描述的姿态运动学方程和以四元数描述的姿态运动方程。这两种描述方法各有优缺点：欧拉角描述的运动学方程在大角度姿态机动时有可能出现奇异，而且运动学方程是非线性的，不易求解。为此，假定分别为fI变换到fC的四元数和系数阵，C的姿态运动学方程表示为：其中QC为四元数初值。
的姿态动力学和运动学方程_交会对接制导与控
C的旋转动力学方程为
其中ωC=［ωcx，ωcy，ωcz］T、TC=［Tcx，Tcy，Tcz］T、TCd=［Tcdx，Tcdy，Tcdz］T、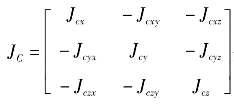
分别为C的旋转角速度、控制力矩、干扰力矩和C的转动惯量，ωC（t0）为角速度初值。
当C为关于xc zc面对称的刚体结构时，Jcxy=Jcyz=0，式（2.23）可展开为
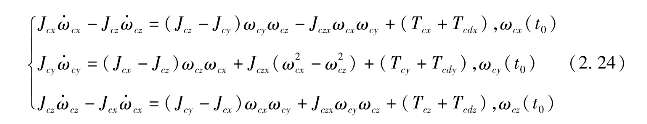
其中，ωcx（t0），ωcy（t0），ωcz（t0）为转动角速度初值。
飞行器的姿态运动学方程有多种描述形式，常用的有采用欧拉角描述的姿态运动学方程和以四元数描述的姿态运动方程。这两种描述方法各有优缺点：欧拉角描述的运动学方程在大角度姿态机动时有可能出现奇异，而且运动学方程是非线性的，不易求解。四元数描述的运动方程避免了奇异现象，而且系统的运动学方程是线性的，易求解。但是，欧拉角相比于四元数具有明显的物理意义，方便直接应用于控制系统。
采用欧拉角描述的C姿态运动学方程为
其中øc，θc，φc分别为C相对于fI的滚转角、俯仰角和偏航角，ø·c，θ·c，φ·c为姿态角变化率。根据式（2.25），由角速度ωcx，ωcy，ωcz可进一步计算得到øc，θc，φc。但是，当θc=90°时，方程会出现奇异，给解算造成不便。
如果采用四元数描述C的姿态运动学方程，可避免发生奇异现象。为此，假定分别为fI变换到fC的四元数和系数阵，C的姿态运动学方程表示为：
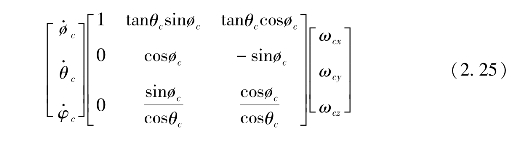
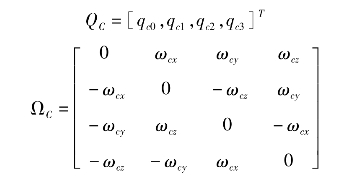
其中QC（t0）为四元数初值。假设fI到fC的转序和转角为zI（φc）→y′I（θc）→xI（øc），则
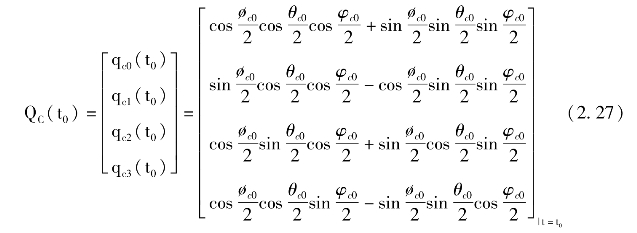
其中øc0，θc0，φc0为姿态角初值。由此得fI到fC的正交变换阵为
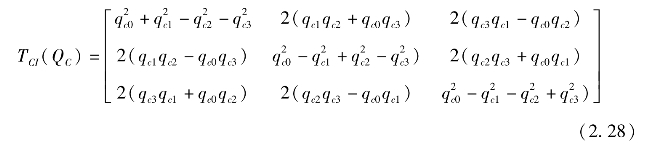
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
