【摘要】:建立C相对T的姿态相对运动模型有两种方法:一种是分别建立C和T的姿态动力学方程,获得ωC及ωT后,再建立C相对T的姿态运动学模型;另外一种是直接建立C相对T的姿态动力学方程,解出相对姿态角速度ωr,再建立C相对T的姿态运动学方程。在上述建立相对姿态运动学方程过程中,姿态运动学方程以四元数描述。同样可以以欧拉角描述相对姿态运动方程,这里不再给出结果。
相对姿态运动模型的建立方法_交会对接制导与控
建立C相对T的姿态相对运动模型有两种方法:一种是分别建立C和T的姿态动力学方程,获得ωC及ωT后,再建立C相对T的姿态运动学模型;另外一种是直接建立C相对T的姿态动力学方程,解出相对姿态角速度ωr,再建立C相对T的姿态运动学方程。
第一种方法,令ωr=[ωrx ωry ωrz]T,ζr=[ør θr φr]T分别为C相对T的转动角速度和姿态角向量,根据式(2.24)、(2.29)分别得到ωC,ωT。
根据fI与fC、fT间的变换关系,有
其中,TCI(QC)、TTI(QT)分别为fI与fC、fT之间的转换矩阵,如式(2.28)、(2.33)所示。
令Qr=[qr0,qr1,qr2,qr3]T为fT到fC的四元数,则C相对T的姿态运动学方程为
![]()

其中,Qr(t0)为四元数初值,
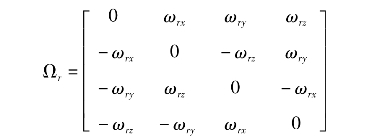
假设fT到fC的转序和转角为zT(φr)→y′T(θr)→xT(ør),则
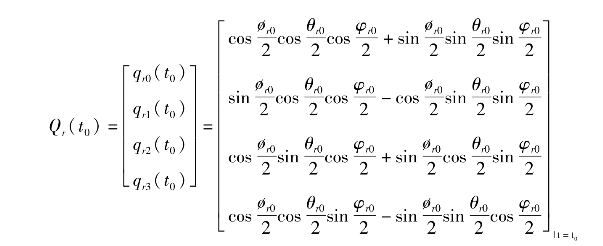
fT到fC的正交变换矩阵可用四元数表示为
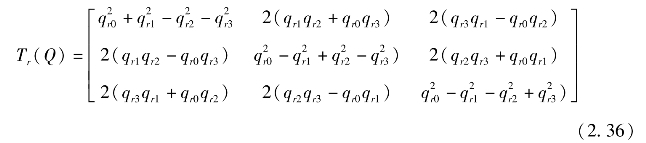
由于四元数没有实际的物理意义,在实际使用中需要将四元数转化为欧拉角,转换关系为[101]:
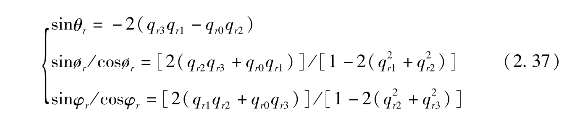
如果θr,ør,φr较小,则qr0≈1,qr1≈ør/2,qr2≈θr/2,qr3≈φr/2。
在上述建立相对姿态运动学方程过程中,姿态运动学方程以四元数描述。同样可以以欧拉角描述相对姿态运动方程,这里不再给出结果。

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
















