单向收敛区域确定

滑动模态的吸引区域实质是保证到达条件成立的区域。对于确定性系统可以采用前述方法确定系统的吸引区域。对于含有不确定性的系统，需要对滑动模态的吸引区域进行估计［106，130～132］。同理，为了保证单向收敛条件的成立，可以对系统初始状态的范围进行限定，即确定系统的单向收敛区域。

1.重新确定吸引区域

在控制受限情况下，由传统到达条件可以确定系统的吸引区域，但是出发于该吸引区域的系统状态未必能到达滑动模态。为此，文献［133］针对式（5.1）～（5.2）组成的系统，提出了一种新的到达条件，重新确定了系统的吸引区域Ω。

根据上述介绍，系统的滑动模态在滑模面上的边界点为A（－k／w，ck／w），B（k／w，－ck／w），其中w=a1－a2 c－c2。

新的到达条件为

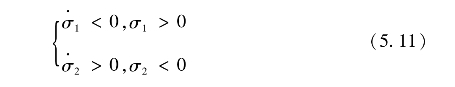
其中，

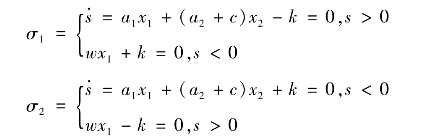
对于式（5.1）～（5.3）组成的系统，由式（5.11）确定的吸引区域Ω如图36所示。若式（5.2）中c=1时，系统的滑动模态存在区域为AB，吸引区域为ACEBDF，上述各点的坐标分别为（－1，1），（－1，0），（0.5，－1.5），（1，－1），（1，0），（－0.5，1.5）。若式（5.2）中c=0.5时，系统的滑动模态存在区域为A’B’，吸引区域为A’C’E’B’D’F’，各点坐标分别为（－1.6，0.8），（－1.6，0），（1.28，－1.44），（1.6，－0.8），（1.6，0），（－1.28，1. 44）。对于上述5.2节例1，data1与data2两种初始状态均位于ACEBDF内。但从仿真结果可知，出发于式（5.11）所确定的吸引区域的状态轨线，其收敛过程未必单向收敛。

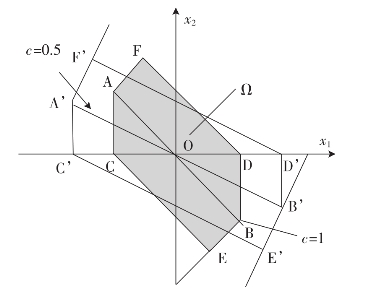
图36　新吸引区域Ω

2.单向收敛区域确定

因为Δd=d－c，根据式（5.1）得

式（5.8）可分段描述为：

当Δd＞0时，要求d·＜0，所以

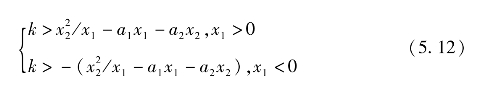
当Δd＜0时，要求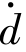＞0，所以

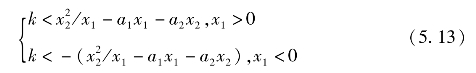
式（5.12），（5.13）所描述的区域可表示为Ω1，该区域能保证d单调收敛到滑模面。对于上述例子，即a1=－1，a2=0，k=2，式（5.12）、（5.13）可分别表示为：

当Δd＞0时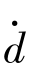，＜0，所以

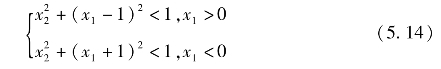
当Δd＜0时，·d＞0，所以

给定任意c，式（5.14），（5.15）所表示的区域Ω1如图37所示，深色阴影区代表Δd＞0的情况，浅色阴影区域代表Δd＜0的情况。

式（5.11）确定的滑动模态吸引区域Ω可保证系统状态到达滑模，但不能保证单向收敛。由式（5.12），（5.13）确定的区域Ω1可保证d单调收敛到c，但到达滑模面上的区域未必是滑动模态。所以，单向收敛区域Ωs为Ω与Ω1的交集，即Ωs=Ω∩Ω{} 1。对于上述例子，图36和图37的交集即为单向收敛区域，如图38所示。当c=1时，单向收敛区域为ACO（x1＜0）+BDO（x1＞0）。当c=0.5时，单向收敛区域为A’C’O（x1＜0）+B’D’O（x1＞0）。

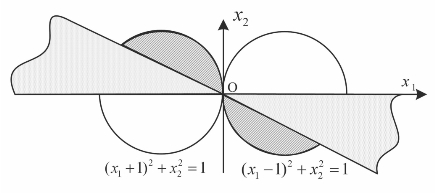
图37　由单向收敛条件确定区域Ω1

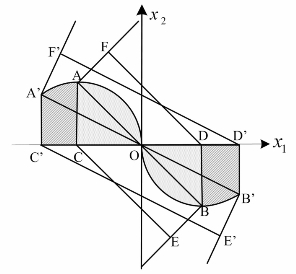
图38　单向收敛区域Ωs

单向收敛区域提供了一个保证x1单向收敛到滑动模态的初始状态范围。若系统初始状态在该区域内，x1必定能单向收敛。若系统初始状态不在该区域内，在系统运行过程中，系统状态也可能进入单向收敛区域并实现单向收敛。所以，系统初始状态位于单向收敛区域是单向收敛的充分条件，而不是必要条件。

上述单向收敛条件和单向收敛区域仅适于系统初始状态位于相平面二、四象限的情况，当系统初始状态位于相平面一、三象限时，需要重新确定单向收敛条件和单向收敛区域。在交会对接系统中，若出现距离和速率同号的情况（位于相平面的一、三象限），控制过程总是先使速度值减小，而后再使速度变号（进入二、四象限），以实现距离减小的目的。所以，上述适于初始状态位于相平面二、四象限的研究可以满足应用需求。