非线性盈亏分析模型

第三节　非线性盈亏分析模型

一、基本思想及模型

在企业营销实践中，往往可以在销售价格上采取一些灵活的策略，如当用户购买量大时，实行优惠价格，打一定的折扣，还有灵活的工资奖励方式，如较高的加班工资等。这时销售收入、产品总成本随产量不呈线性变化，而呈非线性变化。在这种情况下，确定合理的生产规模就比销售收入、产品总成本随产量呈线性变化时要复杂些，如图5－9所示。

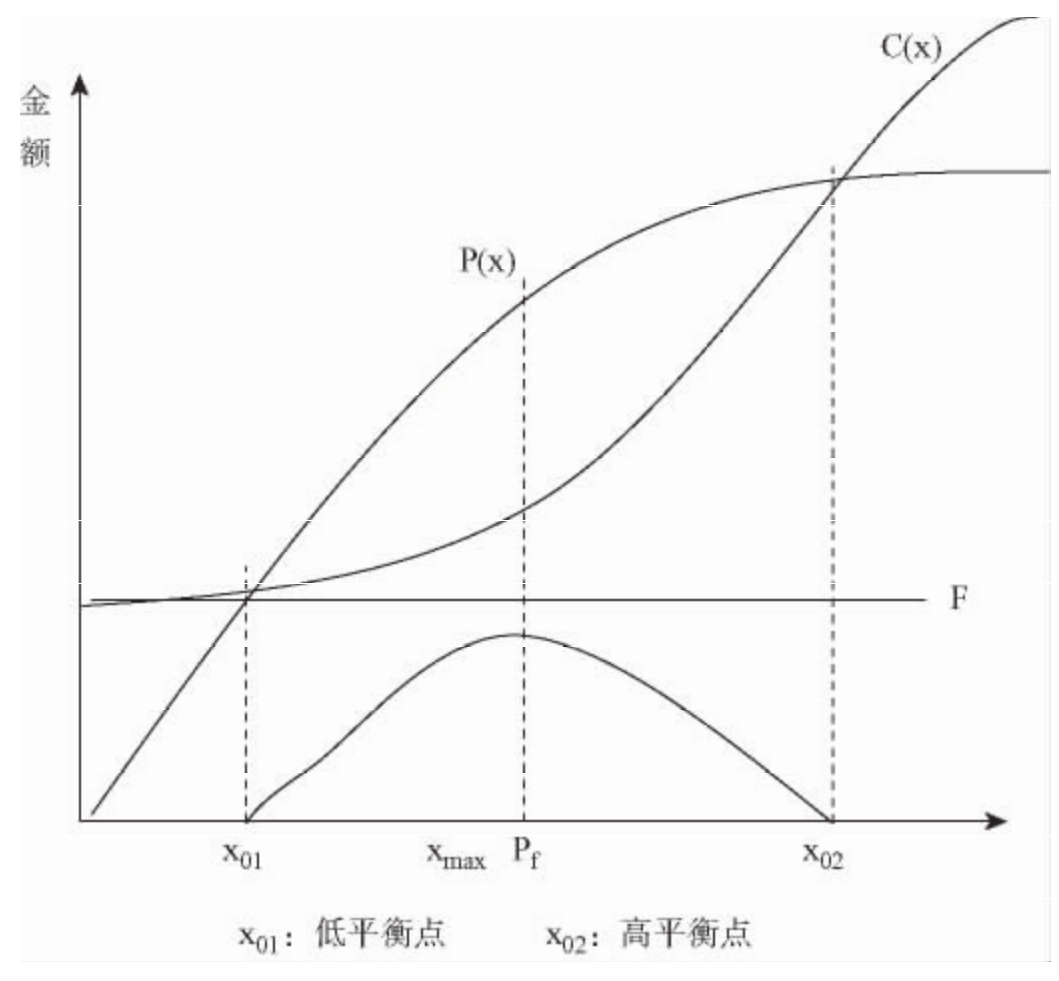
图5－9　非线性盈亏平衡图

从图5－9中可以看出:总成本是产量的非线性函数，用C(x)表示;销售收入也是产量的非线性函数，用P(x)表示。这两个函数的曲线相交于x₀₁、x₀₂两点。x₀₁是第一盈亏平衡点，即最小产量;x₀₂是第二个盈亏平衡点，即最大产量。说明企业要获取利润，其产品产量应确定在x₀₁与x₀₂之间，即x₀₁≤x≤x₀₂。

当利润最大时，利润函数对产量的一阶导数为0，而这时的二阶导数小于零(有极大值)，求出的这个产量就是利润值为最大时的产量。具体计算如下:

E(x)=P(x)－C(x)　　　　　　［E(x)代表利润函数］

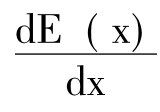=P'(x)－C'(x)

令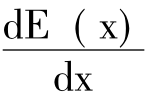=0，求出极值点:

如果＜0

此时的产量为利润最大时的产量。

用同样的办法可以求出单位成本最低时的产量。具体算法为:

平均单位成本C₀=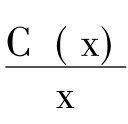==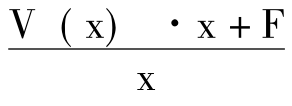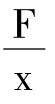+V(x)

令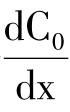=0解出X值，若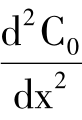＞0时，此时产量为单位成本最低时的产量。

在一定条件下，也可通过P(x)=C(x)，求出x₀₁、x₀₂，则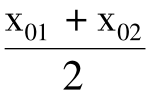为利润最大时的产量。一般地，非线性条件下的盈亏分析技巧多采用方程ax²+bx+c=0，如此求解较为简便。

二、应用实例

例1:已知甲、乙两种产品预测数据如表5－9所示。已知材料费用由于大量采购可以得到折扣的优惠:材料费－0.001x(x为采购量)，购买产品的单位售价也可因购买量增大给予折扣:P－0.0035x(x为购买量)，试求各方案的经济临界产量。

表5－9　甲、乙两种产品预测数据表　　单位:元

解:

(1)由题中所涉及的价格、变动费为两个变量而非一个定常数，故采用非线性盈亏分析模型，而不能用线性形态下保本点的计算公式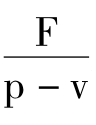(x=或x=)。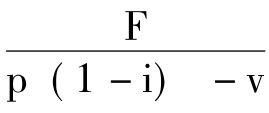

(2)求解这一问题采用的公式为:

销售收入函数=总成本函数

即P(x)=C(x)

(3)设X为经济临界点产量或销量，则:

甲产品:

销售收入函数P_甲(x)=50x－0.0035x·x

0.0035x为折扣掉的部分，也即企业少收入的部分，单价随购买量的变化而变化，故应视为一个不定常数。

总成本函数C_甲(x)=60000+［10x+(15x－0.001x·x)］

若令P_甲(x)=C_甲(x)，则有如下方程:

50x－0.0035x²=60000+(25x－0.001x²)

25x－0.0025x²－60000=0

0.0025x²－25x+60000=0

解此方程得:

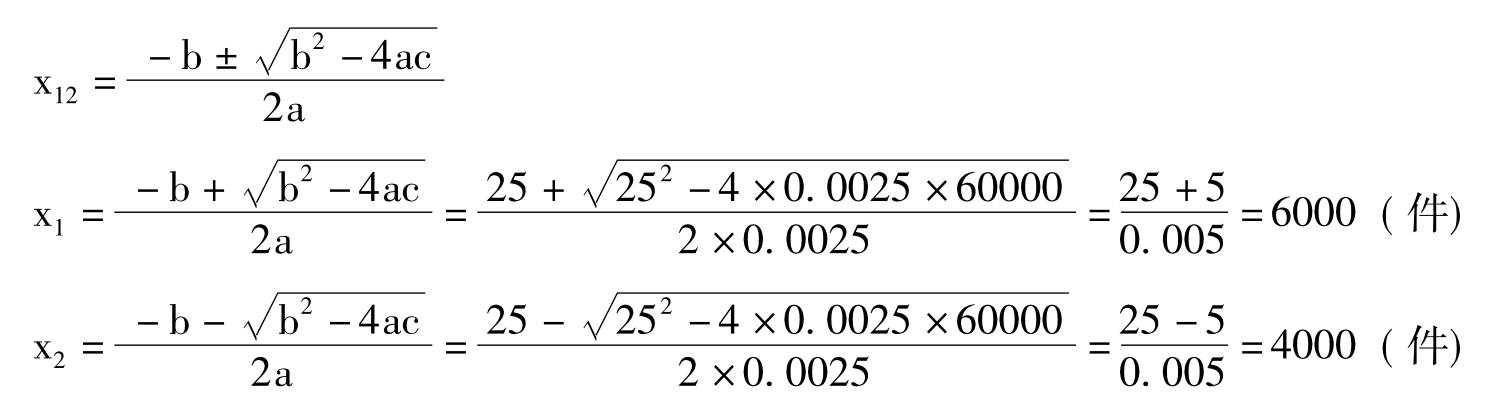
则:甲产品经济临界产量分别为6000件和4000件，即低平衡点:4000件，高平衡点:6000件。

乙产品:

销售收入函数P_乙(x)=55x－0.0035x·x

总成本函数C(x)=69300+［10x+(18x－0.001x²)］_乙

若令P_乙(x)=C_乙(x)

则55x－0.0035x²=69300+(28x－0.001x²)

整理后:0.0025x²－27x+69300=0

Δ=b²－4ac=(－27)²－4×0.0025×69300=729－693=36＞0

故方程有两个不相等的实数根:

则乙产品的临界点产量分别为4200件和6600件。

例2:已知某产品固定成本F=10000元，单位可变成本V=40元/件，售价P=60元/件。当销量x增加，售价按(60－0.001x)元/件下降，试求利润最大时的销售量x_A。

解:

∵利润P_f(x)=P(x)－C(x)

　　　　　 =(60－0.001x)·x－(10000+40x)

　　　　　 =－0.001x²+20x－10000

一次求导: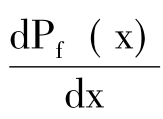=－0.002x+20=0

则

x=10000(件)

二次求导: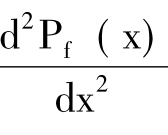=－0.002＜0，有极大值

∴x=x_A=10000件

此时最大利润P_f(x)=－0.001×(10000)²+20×10000－10000

　　　　　　　　 =90000(元)

例3:某企业的总销售额与生产成本均是产量的函数，已知其非线性方程为:S= 100Q－0.001Q²;C=200000+4Q+0.005Q²。试求该企业的盈亏平衡点的产量和最大利润时的产量。

解:

(1)求盈亏平衡点的产量。

S－C=(－0.001－0.005)Q²+(100－4)Q－200000=0

－0.006Q²+96Q－200000=0

解二次方程得:Q₁=2477Q₂=13533

(2)最大利润时的产量Q_max

2×(－0.001－0.005)Q+100－4=0(求导)

－0.012Q+96=0

故Q_max=8000元