股价特质风险的分解及统计特征

第四章　股价特质风险的分解及统计特征

在许多关于风险和收益的理论研究中，总体波动无疑都是很重要的研究内容，因为它反映了市场的整体风险。但是市场总体波动只构成了股票资产波动来源的一部分，行业水平波动、企业特质水平波动也是股票波动成分的另外两个组成部分。为了研究清楚股票的波动现象，有理由也有必要去关注这些不同层面波动成分的风险变化规律。

然而比较遗憾的是，涉及行业波动和特质风险的经验研究在已有文献中仍相对缺乏，本书对股价特质风险的实证分析将从对股票波动成分的分解开始。在股票各波动成分的基础上，本章将展开对股价特质风险的趋势分析以及实证研究股票资产（组合）各波动成分（尤其是特质风险）具有的风险波动特征。

第一节　股票资产波动成分的趋势变动分析

本章首先为市场、行业和企业层面的波动计算获取时序数据，计算的波动分解方法在本书第三章做了仔细阐述。相比已有文献有所改进的是，本书并不需要对行业或企业涉及的协方差、β系数进行估算。而且出于简化的目的，本章计算依旧遵循Merton（1980）、Poterba and Summers （1986）、French，Schwert and Stambaugh（1987）、Schwert（1989）以及Schwert and Seguin（1990）等的方法，使用1个月内的日度数据来计算该月的样本方差，这种方法的简化之处在于并不涉及参数模型的估计和使用。容易看到这种方法的优越之处，因为多变量波动模型不仅非常复杂，难于估计，而且参数模型的长处在于进行波动预测，而对波动的历史运动过程则较难做出精确和具体的描述。本书所使用的方法计算得出的方差值是对已实现波动过程的较准确数值的刻画，这种方法的计算思路首先被Merton（1980）提出，经过Nelson（1992）和Clmx（2001）的认真改进，使得方法的计算精度在原始思路上获得很大提高。

一、股票资产组合的选取与相关数据说明

根据数据的可获得性，并参考论述的针对性、有效性，本书以中国股票市场作为问题论述的主要研究对象。依据我国股市自身的行业特点，结合CRSP及CSMAR等数据库划分行业属性的习惯，本书将我国股市分成：农、林、牧、渔业，采掘业，制造业，电力、煤气及水的生产和供应业，建筑业，交通运输、仓储业，信息技术业，批发与零售贸易业，金融、保险业，房地产业，社会服务业，传播与文化产业及综合类共13个大类行业。为了分离出较显著的股价特质风险，选取的资产组合不需要也不用将这13个大类的所有股票纳入考虑的范围。具体到本章，样本选取将在制造业，建筑业，交通运输、仓储业，信息技术业以及金融、保险业内进行资产组合。为了检验实证结果的稳健性，本书会在这13个行业类别中对资产组合进行个股数量及所涉行业的调整。

我国上海证券交易所和深圳证券交易所功能作用基本相同，其中的股价走势也具有较强的趋同性，但由于上海证券交易所在投资交易和学术研究等方面受到越来越多的关注，同时也是为了减少问题论述时其他因素对主题的过多干扰，因此本书将主要以上海证券交易所的上市股票作为考察研究的标的对象。

（一）股票资产组合的选取

从前文对股价特质风险的种种理论分析可以知道，股价特质风险主要是针对股票资产组合而言的。因此对股价特质风险的实证研究理所当然首先需要选取股票资产组合作为分析、研究的对象。为了突出特质风险，本书不能采取风险分散化的资产选取。遵循随机原则，并考虑一定对我国经济发展的代表性，本章以这样5个行业的股票资产作为资产组合的来源，即制造业，建筑业，交通运输、仓储业，信息技术业以及金融、保险业。本书还针对样本选取做了稳健性检验，检验发现本书的样本选取不会对本书的研究目的及研究结果产生显著影响。

样本股的选取基本遵循随机原则，但为了保持数据一定的持久性，因此未将最近几年上市的股票纳入资产组合的范围。本章基准的股票资产组合具体包括：

制造业选取的个股包括武钢股份（600005）（股票代码，下同）、东风汽车（600006）、青山纸业（600103）；

建筑业选取的个股包括葛洲坝（600068）、北京城建（600266）、隧道股份（600820）；

交通运输、仓储业选取的股票包括上海机场（600009）、天津港（600717）、中储股份（600787）；

信息技术业选取的个股包括百科集团（曾用名：国能集团等）（600077）、方正科技（600601）、同方股份（600100）；

金融、保险业选取的个股包括浦发银行（600000）、国金证券（600109）、安信信托（600816）。

在资产组合中每个单只个股的份额数相同，因此本书在计算个股的权重系数时可以直接以股票本身的市价总值进行对比计算，不用再考虑个股投资份额不同所形成的影响。

（二）相关数据说明

考虑各样本股票上市时间先后有别，为保证资产组合的一致性，本章将研究的样本区间确定为2001年1月1日到2010年3月31日。

资产收益率的确定方法为：收益率＝（本期价格－上期价格）／上期价格。市价总值本来是指已发行全部普通股按市场价格计算的价值总额，由于我国股市长期以来存在大量非流通的股票份额，而且即使是在股权分置改革之后，上市公司的股票要真正实现全流通也存在一个逐步推进的过程。鉴于我国股市的实际情况，本书将市价总值的计算调整为：市价总值＝股价收盘价×个股的流通股数。这样可以保证利用市价总值计算出来的加权平均系数具有更强的实际约束作用。另外，由于个股停牌的原因，会造成个股在部分月份成交数量减少，这时以个股停牌前最后一个交易日的收盘价计算出来的价值总额作为该个股在停牌期间每天的市价总值，以避免因个股停牌造成个股当月计算出的加权平均系数下降。

本章的数据来源为国泰安研究服务中心研发提供的CSMAR中国股票市场交易数据库、中国股票市场衍生指标数据库和中国债券市场研究数据库、中国国家统计局网站以及中国人民银行网站等。

（三）数据计算的结果

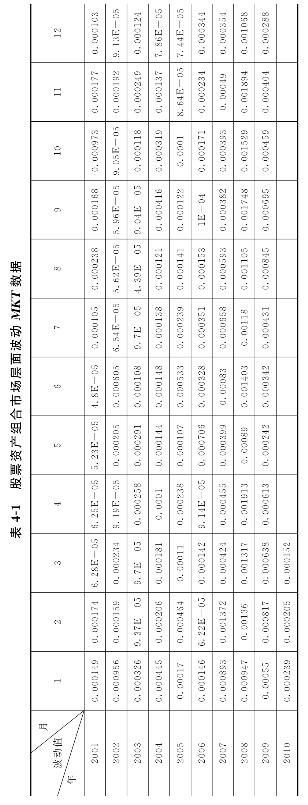
按照上文阐述的计算方法，利用式（3－17）股票资产组合计算出的市场层面波动MKT数据，如表4－1所示：

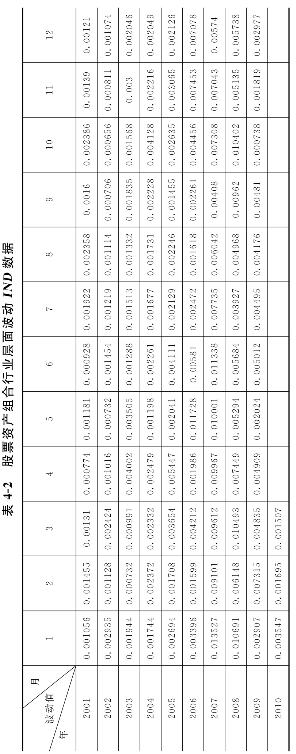
利用式（3－18）和（3－19）计算出行业层面波动IND数据，如表4－2所示：

利用式（3－20）和（3－22）计算出特质风险FIRM（即股价特质风险）数据，如表4－3所示：

以上所有数据均为月度数据，各数据的样本个数均为111个。限于篇幅，本书并未将计算中的日度数据、中间数据和其他变量数据等都一一列出，只是重点将主要分析对象的最终计算结果——各层面的波动数值，用数据表格表示出来。

二、股票资产波动成分的统计描述

接下来本书首先对计算出来的各不同层面的波动成分进行统计性描述，观察它们具有的直观的统计数量特征。

（一）股票资产组合各层面波动成分的图形分析

在资本市场上人们通常会认为市场波动随着时间推移和市场发展波动会越来越剧烈，这种认识并不尽然。市场层面的波动并不会表现出随时间增长而出现的系统性趋势。即使在某些时间段，特别是在受到金融危机影响的条件下市场层面波动可能会呈现波动幅度增加的现象，如图4－1所示的图形描述中可以看到，这种波动幅度增大并不会持续很长时间。市场层面波动的这一波动特性在一定程度上也验证了Schwert（1989）针对这一问题所做的专门阐述。

图4-1　股票资产组合市场波动 MKT

图4－1中描绘了股票资产组合市场层面波动的图形。图4－1（a）是用式（3－17）计算出的市场波动值，图4－1（b）是滞后12期经过指数平滑后的市场波动曲线。从市场层面波动的图形特点可以看出，市场层面的波动确实会受到较大金融风波的冲击。如2008年9月起由于美国次贷危机的影响，我国股票市场也迅速受到金融危机的冲击，市场层面波动幅度在继2008年上半年发生历史性最大波幅^[1]之后又接着发生了幅度明显的增大，最大波动幅度再次接近前期最高波幅。随着国家干预经济发展的各项政策措施的出台，以及经济环境的逐步稳定，市场层面波动又逐步趋于稳定。从样本期的全时期过程来看，股票市场层面的波动虽然说也会受到经济发展基本面的冲击及影响，但市场层面波动也确实没有呈现出某种长时期的趋势特点。从2001年1月到2010年3月，股票资产组合市场波动的波动平均值只有0．04%，远小于行业波动的10．56%和个股特质风险波动的15．66%。而通过（a）、（b）图之间的对比可以看到，市场波动拥有一个移动较慢的成分，但同时也具有很清楚的高频波动噪声。

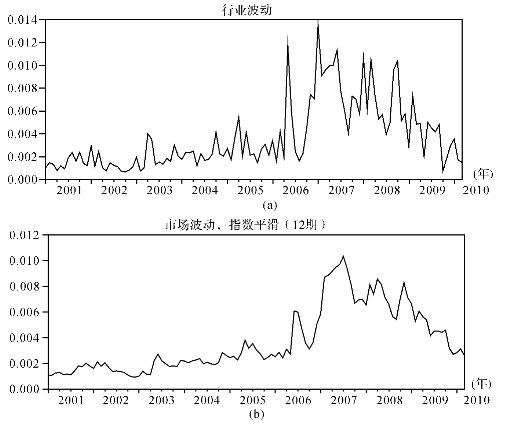
图4－2　股票资产组合行业波动IND

图4－2考察了行业波动IND的变动规律。

图4－2（a）是利用式（3－18）和（3－19）计算出来的股票行业波动，表现的是每日行业收益相对市场收益而计算出来的每月波动方差大小值。图4－2 （b）是经过12期指数平滑后行业波动的曲线。

相比市场波动，行业波动在平均幅度上要比市场波动高出许多。这与资本资产定价模型CAPM对于相关问题的认识与解答是一致的。和市场波动MKT相似的是，行业波动也拥有一个移动较慢成分及相对高频的噪声。行业波动幅度的变化基本和市场波动具有相同的变化时刻，其变化轨迹也具有一定的相似性。但仔细观察图4－2及参考图4－3也可以发现，行业波动的波动增加及减小相较市场波动而言要提前稍许时间，这可以在一定程度上说明行业波动比市场波动更具有信息变化的敏感反应特性。从行业波动与市场波动存在的不完全一致的波动形状里，能够判断出市场波动反映出更多的市场基本面变动的信息；而行业波动则更像企业波动，反映出更多的企业经营发展及未来预期现金流的变化信息。

图4－3　股票资产组合企业波动FIRM

图4－3描绘的是企业层面波动（FIRM），即股价特质风险波动。

图4－3（a）是利用式（3－20）—（3－22）计算出来的股票企业波动，表现的是每日企业收益相对企业所处行业收益而计算出来的每月波动方差大小值。图4－3（b）是经过12期指数平滑后企业波动的曲线。

特质风险表现出的最突出特征就是它比市场波动（MKT）和行业波动（IND）平均波动幅度都要大。这一特征意味着股票总体波动风险中特质（企业）风险是占据了最大成分及比例的波动风险成分。特质风险的第二个重要特征是特质风险在样本期内表现出较明显的趋势变动，这和市场波动的随机漫步特点具有很大区别，图形上的这些区别为我们更形象地展示了股价特质风险是股票资产风险因素主要来源的这一理论事实。股价特质风险在很大程度上内在主导了股票总体风险趋势的变化。同时与市场波动及行业波动相比较还可看到，特质风险的波动变化与行业波动更为相似，这既可以从资本资产定价的角度进行理解、分析，同时也可佐证股价特质风险到底源自何处。

将3个层面的波动放在一起再做比较，比较清楚的是低频数据，即经过指数平滑后的波动变化三者基本趋于一致运动，这从图4－1、图4－2和图4－3（b）都可以很清楚地看出。但是加入包含各自波动信息的高频部分后，3个波动成分就表现出其具有不同运动变化规律。如在2001年至2002年间，市场波动波幅增大约为该时间段前后波幅的3倍；行业和企业波动（尤其是行业波动）则相对增加得并不很多。这一差异更能充分表明市场波动容易反映出宏观经济基本面的变化，特别是资本市场由此受到的冲击与影响。如我国在2001年受国际环境的影响，经济增长率逐季下滑，物价在2001年底再次出现负增长。与此同时广义货币M2与GDP的比率却还在不断上升，2000年这一比率为1．5，2001年达到了1．65，2002年又进一步上升为1．97。最终中国人民银行于2002年2月21日连续第8次下调利率，如表4－4所示，促使储蓄分流，这一时段全国股民开户数不断增加，形成了一场股票市场发展的高峰。而从2003年开始，我国股市基本已进入熊市阶段，市场波动幅度小而且基本平稳，但行业及企业波动则是一路走高，呈现清晰的上升趋势。并且行业及企业波动比市场波动于2007年提前达到波动的最高值，此后虽然仍受到了国际金融危机的冲击，但行业及企业波动的总体水平却又比市场波动更早进入图形的下降通道之中。从3种波动成分的变动差异中可初步总结出这样一些规律：如果说市场波动更容易反映资本市场受到宏观经济基本面影响而产生变动的一些信息，那么行业和企业波动则更能反映上市公司受到经营环境制约而形成的对未来经营结果的诸多预期。因此3种波动成分波动的步调并不会一致，行业和企业波动除在波动幅度上较市场波动为大之外，前两者由于自身包含了更多的预期信息，因而在波动变化的时间上还要明显领先于市场波动。

表4－4　2002年中国人民银行连续第8次降息情况表

注：“－”号意味着利率水平下调或利差减少。
资料来源：中国人民银行统计司：《中国人民银行年报2002》。

（二）变动样本资产组合各波动成分的描述性统计及其对比

表4－5给出了市场、行业和企业3个层面波动成分的描述性统计值，从图形分析中观察得出的结论也得到了具体统计数据的再次印证。从平均值和标准差来看，行业和企业（特质风险）波动要明显大于市场波动。行业波动在波动幅度和波动的剧烈程度上接近企业波动，但从偏度和峰度值的大小看行业波动并没有完全包含企业波动的所有信息，相反行业波动将特质风险信息保留在了企业波动当中，其自身波动的随机性要比企业波动更强。因此基于这样的原因，对于股价特质风险的把握和进一步研究也将是以企业波动作为主要的研究对象。

表4－5　波动成分的描述性统计值

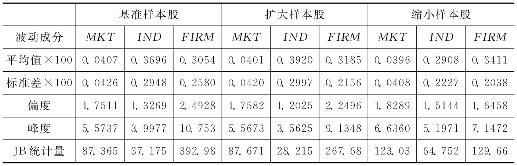
注：本表列出的是股票各波动成分的描述性统计值。MKT是市场波动，通过式（3－17）计算得出；IND是行业波动，通过式（3－18）和（3－19）计算得出；FIRM是企业波动，通过式（3－20）—（3－22）计算得出。表中的平均值与标准差均在原值的基础上乘以100。

另外，为了检验之前选取的基准样本股所得有关结论的准确性以及稳健性，样本股选取可将基准样本股进行两个方向的调整。即扩大样本股以获得更大范围的股票资产组合，和缩小样本股减少股票资产组合的规模。扩大样本股增加了房地产业和社会服务业两个行业，增加的个股包括属于房地产业的浙江广厦（600052）、浦东金桥（600639）、陆家嘴（600663），和属于社会服务业的中国国贸（600007）、黄山旅游（600054）、中青旅（600138）。缩小样本股去掉了两个占比相对大的行业即金融、保险业和建筑业，去掉的个股包括属于金融、保险业的浦发银行（600000）、国金证券（600109）、安信信托（600816），以及属于建筑业的葛洲坝（600068）、北京城建（600266）、隧道股份（600820）。在对样本股进行调整后，依然采用基准样本股的计算方法，计算得出了扩大样本股和缩小样本股的描述性统计量^[2]。通过表4－5的数据对比可以发现，改变样本股的构成及其大小范围，并不会改变此前对各波动成分所做的分析结论，计算结果再次支持了前文做出的有关论述及判断。同时各样本股之间相同统计量间的大小变化并不明显，这说明在我国资本市场分散投资，至少在股市内部效果并不明显。其中尤其是股价特质风险，从表4－5中的数据对比变化结果显示，企业波动并不随样本股所含行业及个股数量的增减而发生相反变化，即分散投资并不能降低或减小股价特质风险的总体水平。本书通过计算过程可以判断，企业波动也即股价特质风险的大小变化和加入股票资产组合的具体行业乃至具体个股密切相关，这说明企业层面上的风险水平与企业自身特点包括经营效果有着紧密的内在联系，特质风险是通过企业层面反映出来的信息不确定性，它用传统的CAPM系列及APT定价模型较难进行合理解释。本书认为，股价特质风险需要将其纳入新的股票资产定价模型之中，股价特质风险的变化机制需要学者们利用新的方法和采用新的视角来对其做深入研究。

（三）股票资产波动成分的趋势分析

波动成分的统计描述已阐述了市场波动的随机性和行业、企业波动的趋势变化特征。由于这一问题关系到对特质风险波动特征的实证分析，因此这里对其再做进一步的讨论。

表4－6给出了各层面波动的自相关系数表。从表4－6中的数据能够看到，各波动成分均表现出了很强的序列自相关性。这也说明各波动成分存在非平稳时间序列及含有单位根的可能性很大。本书首先对市场波动MKT进行具体考察。

表4－6　波动成分自相关系数表

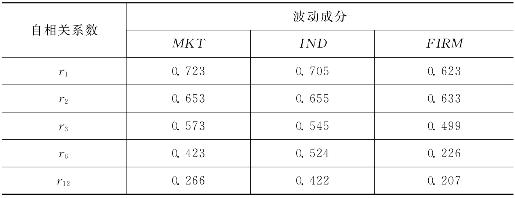
注：本表列示的是各波动成分的自相关系数。MKT是市场波动，通过式（3－17）计算得出；IND是行业波动，通过式（3－18）和（3－19）计算得出；FIRM是企业波动，通过式（3－20）—（3－22）计算得出。ri代表第i月的自相关系数。

1．市场波动MKT的平稳性及其AR（2）模型描述

市场波动自相关和偏自相关分析图如图4－4所示。

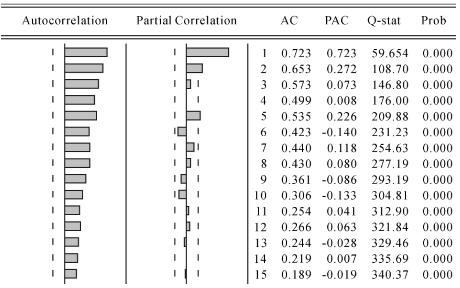
图4－4　市场波动MKT自相关与偏自相关分析图

从图4－4中可以看到市场波动MKT的自相关系数在各阶间呈现出拖尾现象，而偏自相关系数在二阶处截尾。因为对于AR（p）模型其偏自相关系数φk，k的最高阶数为p，也即AR（p）模型的偏自相关系数为p阶截尾。因而可以判断市场波动MKT满足一个AR（2）过程。对其进行建模，其模型等式为：

MKTt＝0．000411＋0．525（MKTt－1－0．000411）

R2＝0．5616　D．W．＝2．041

注：＊＊，＊＊＊分别表示在5%和1%的显著性水平下通过检验。

市场波动MKT的拟合值与模型回归残差的序列图如图4－5所示：

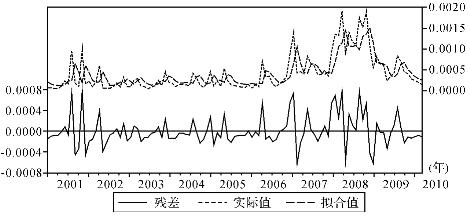
图4－5　市场波动MKT和残差序列图

图4－5清楚表明AR（2）模型较好地拟合了市场波动MKT的变化，模型回归的残差序列从图形上看基本也是围绕零均值随机上下波动的平稳时间序列。如图4－6所示的χ2检验结果可以直观看出市场波动AR（2）模型的残差序列其自相关系数和偏自相关系数已不存在序列相关。进一步，由于残差序列样本量n为109，最大滞后期m可以取作［109／10］或者，取m为11。从滞后期11这一行可以看到，检验统计量Q值等于14．140，其相伴概率的值为0．117，不能拒绝原假设。通过χ2检验的检验值大小，同样可以表明市场波动AR（2）模型残差序列相互独立，模型较好地拟合了市场波动MKT的变动规律。

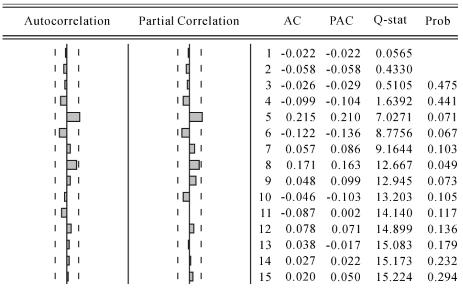
图4－6　市场波动（MKT）AR（2）模型残差序列相关图

2．行业波动IND和企业波动FIRM的平稳性检验及其趋势变动分析

接下来再对3层面波动的平稳性进行综合检验。尤其是要看看行业波动IND和企业波动FIRM作为时间序列其是否也属平稳时间序列的范畴，若不是，那么它们会具有怎样的趋势变化特征？

（1）平稳性检验。

为检验各波动序列的平稳性，采用Augmented　Dickey and Fuller （1979）检验法来对各波动序列进行单位根检验。表4－7列出了ADF单位根检验的结果。

表4－7　各波动成分单位根检验

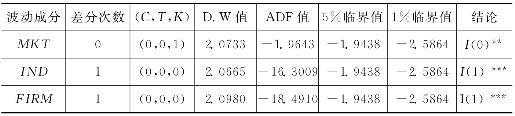
注：（C，T，K）代表ADF检验式的常数项、时间趋势项以及滞后期数；＊＊、＊＊＊分别表示在5%和1%的显著性水平上通过检验。

表4－7中各波动成分的单位根检验结果表明确如上文推断和模型描述的，市场波动MKT是零阶单整时间序列，即股票资产组合市场层面的波动在样本期内基本属于平稳时间序列，并不具有明显的趋势变化特点。而行业波动IND及企业波动FIRM均是一阶单整时间序列，其原序列即水平数据在5%的显著性水平之内均存在单位根^[3]。这一单位根的检验结论说明，在我国股市范围内股票资产组合的行业波动以及股价特质风险具有较明显的趋势变化特征。这种趋势变动规律表明，股价特质风险波动具有波动变化的持续性，这种持续性已大大超出了传统金融（以EMH理论为代表）对股价变化规律给出的解释能力，而和投资者行为对股价影响的表现有很大的相似性（Hirshleifer，2001）。关于波动趋势变动的问题Vogelsang （1998）提出过一种Wald类型的趋势回归模型：

式中v∈｛MKT，IND，FIRM｝；μ是截距项；g是线性趋势系数；ut是误差项；d（L）是无限移动平均系数，大小等于，L是滞后算子；et是白噪声信息。这一检验方法对判断I（1）序列的线性时间趋势具有较强的稳健性。但缺点也较明显，Vogel　sang的方法对于具有一定周期特点，呈现非线性随机趋势变化的时间序列其检验的办法偏于单一。本书借鉴Vogel　sang的回归模型思路，但采用去除趋势法的方法对行业和企业波动做趋势变化的分析。

（2）趋势变动成分分解。

利用计量经济学软件Eviews　6．0先对本书的行业波动和企业波动进行Census×12的季节调整，剔出其中包含的季节和不规则因素。在季节调整的基础上，利用HP滤波分离出行业、企业波动的趋势变动成分

，行业、企业波动的循环（随机）变动成分可以由式（4－3）求出。行业和企业波动的HP滤波分析结果如图4－7和图4－8所示。

图4－7、图4－8的上半部分显示的是行业与企业波动趋势变动的成分，即和，下半部分显示的是两个原序列循环（随机）变动的成分，即和。

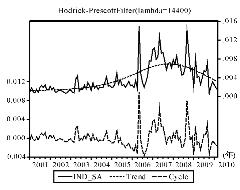
图4－7　行业波动趋势分解结果

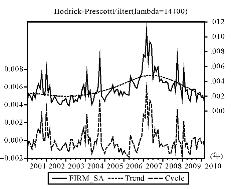
图4－8　企业波动趋势分解结果

图4－7和图4－8显示的是波动水平值（经季节调整）与趋势成分值之间形成的差额变化。在宏观经济的经济周期研究里也将其称作绝对量产出缺口。由于相对值便于不同数据间的比较，因此也可将相对量的差额变化计算出来并绘成图形。相对差额变化可用来表示，计算公式为：

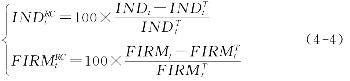
而相对差额变化的图形如图4－9和图4－10所示：

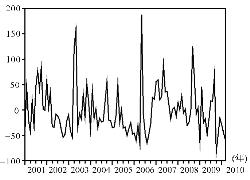
图4－9　行业波动相对差额变化

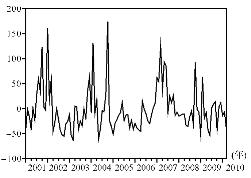
图4－10　企业波动相对差额变化

（3）行业波动IND和企业波动FIRM的趋势变动分析。

和市场波动MKT属于平稳时间序列不一样的是，行业波动IND和企业波动FIRM的单位根检验证明它们的数据水平值存在单位根，只有通过一阶差分之后它们的单位根检验才能获得通过。因此，我们基本可以判断在我国股票市场上，股票资产行业波动以及企业波动的时序数据是一种非平稳的时间序列。这意味着在行业和企业层面的股价波动变化中存在持续性特点，有着区别于市场随机变化的趋势变动过程。这一发现不仅验证了本书在前面理论分析章节中的有关理论背景分析，而且对于股票行业波动及企业波动趋势变动规律的总结为本书后续研究分析的展开铺垫了实证基础。

行业波动与企业波动趋势变动具有相同或相似的地方是：

首先，从HP滤波的分解结果来看，行业与企业波动都存在明显的趋势变动过程，并且这一趋势变动过程基本与我国宏观经济环境的总体变化较为一致。见图4－7和图4－8，从2001年到2007年的大部分时间里行业与企业波动基本都呈现波动幅度不断增大的变化趋势。^[4]而从2007年底开始我国股票资产行业波动与特质风险在先后达到波动最大值后，均早于美国次贷危机的全面爆发提前进入趋势下降的变化过程当中。

其次，假如排除掉美国次贷危机的影响，即如果只将考察的期限限定在2008年以前，那么趋势分析能够发现行业与企业层面的波动基本会受到经济发展（包括资本市场的不断改革和发展）的影响表现出趋向增大的变动趋势。

最后，在利用HP滤波去除趋势成分后，行业与企业波动的随机波动成分能初步表明，在随机波动循环变化的背后，行业与企业层面的股价波动都受到我国股票市场多层面来源信息不确定性的影响与冲击。^[5]

行业波动与企业波动趋势变动存在的区别与不同是：

第一，行业波动与企业波动的波动幅度存在差别。企业波动在波动幅度上平均起来要比行业波动高；

第二，企业波动发生大幅度波动的次数及频率相比行业波动要多出许多；

第三，从两波动值相对差额变化的图形对比来看，行业波动多发生正向的偏离（指偏离趋势值），差额值较大；而企业波动多存在负向的偏离，差额值较小。

可以看到，行业波动在包含许多市场层面波动信息的同时，也吸收了很多来源于企业层面的不确定信息，行业波动介于两层面波动的当中，其波动特点兼而有之。那么行业波动还体现了哪些自身特点？本章下一节通过不同行业及企业之间的比较，获取有关结论。

第二节　股票资产行业内波动成分的比较分析

上一节研究了跨行业的各层面波动成分的一些波动规律，这些各层面的波动成分实际上是各行业间平均计算的波动水平。尽管这些平均波动包含了跨行业各层面的波动信息，但其存在的明显缺点是不能通过平均水平的波动来具体反映股票资产中各单一行业的风险波动情况。因此，本节将通过计算各单个行业的行业波动与企业波动，来对行业特点对波动成分形成的影响进行比较和分析。同时通过了解特质风险在各行业和各企业间的变化差异，更为全面地把握特质风险变化、波动的影响机制。

本节将上文的样本股扩大至7个行业作为这里的研究对象，即分别是制造业，建筑业，交通运输、仓储业，信息技术业，金融、保险业，房地产业和社会服务业。

一、单个行业内各波动成分的方差计算

（一）数据与计算说明

为简化计算，也为方便比较，本节计算采用的数据与本章第一节扩大样本股的来源数据一致。

按照计算方法的先后顺序，本书将各波动成分的数据计算过程说明如下：

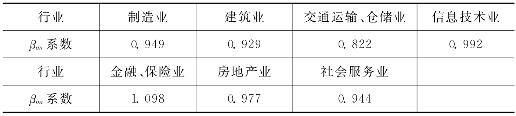
第一，根据式（3－26）分别对各行业的超额收益Rit做回归分析，可计算获得各行业的βim风险系数，结果如表4－8所示：

表4－8　各行业βim风险系数表

在计算各行业βim风险系数的过程中，实际上在各方程的回归结果里也同时获取了式（3－26）的残差序列）数据；

第二，将获得的残差数据按照式（3－18）的方法计算的方差值；

第三，通过式（3－26）和（3－27）的比较，计算出单个行业中企业超额收益的值；

第四，将获得的序列值同样按照式（3－20）和（3－21）的方法计算的方差值；

第五，按照式（3－28）将以上计算出来的结果进行相应代数运算，运算结果即为各单个行业的行业层面波动数值；

第六，按照式（3－29）将上述有关的计算结果进行相应计算，结果即为各单个行业企业层面的波动数值（各行业内平均水平的）。

（二）波动成分的计算结果

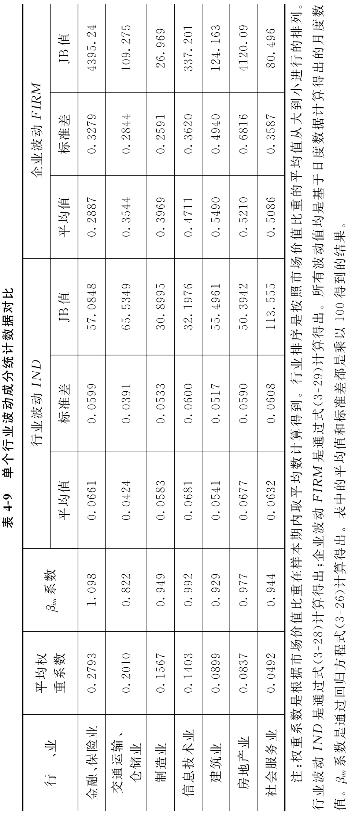
限于篇幅，单个行业内各波动成分的计算结果在正文中未予列示，但作为参考，本书仍把行业及企业的波动原始数据结果列在了本书附录中。如表4－9所示直接给出各波动成分的统计性数据，以此进行对比分析。

二、行业内各波动成分的比较分析

表4－9中各行业是按照平均权重系数从大到小进行的排列，在样本组合中比重最大的要数金融、保险行业，这与我国股市上普遍的投资常识相一致。我国股市上金融股的走势很多时候往往引领了市场的整体走向，金融股往往是大盘股，常常也是各种投资基金的重仓股之一。排在金融、保险行业之后的依次是交通运输、仓储业，制造业，信息技术业，建筑业，房地产业和社会服务业。从表4－9所列数据间的对比，本书分析归纳出如下结论。

（一）行业内企业波动仍比行业波动明显

通过表4－9中行业波动与企业波动平均值与标准差的数据对比，能清楚地看到各行业的特质风险明显要比行业层面波动大许多。企业波动在波动水平（以平均值为代表）和波动幅度（以标准差为代表）两方面均高出行业波动近10倍左右。企业波动明显较大的JB值还表明企业波动数值远不具有正态分布的特性，它代表的股价特质风险变动范围较宽。这一实证结果也再次从行业本身的角度证明了股价特质风险确是股票资产价格非随机、非理性波动的最重要来源之一。

（二）企业波动与行业市场价值权重呈反向变动关系

对比各行业企业波动数值与行业市场价值权重系数之间的变动关系，能够发现权重系数大的行业其特质风险相比较而言幅度更小，而随着权重系数的减小，权重小的行业所包含的特质风险平均而言反而会倾向于逐渐增大。这一规律比较易于用一般的投资直觉进行理解，并且也和成熟资本市场国家获得的发现结果基本一致。企业波动体现出的这一行业性特点具有这样的启示：关注股票资产组合的特质风险波动（变动）需要更关注市值比重较低的个股。这些个股常带有中、小企业和新上市的特点，所属的行业或是基础性行业，或是新兴发展行业。研究这些行业及其个股面临的诸多信息不确定性，是把握特质风险波动的关键环节。

（三）行业波动未表现出明显的行业特点

再观察各行业的行业层面波动。从比较中可以看到，行业波动不仅波动幅度较小，还未表现出较明显的行业特点。行业波动由于系统性风险βim系数差别不大，更多受到股市总体市场风险的影响。同时行业波动差别不大这一特点也可佐证，在我国股票市场上至少在行业层面上显示出，我国股市价格存在市场行情轮动和基于“羊群效应”的股价趋同变化规律（史永东，2003）。

（四）行业系统性风险βim显示出各自的行业差别特点

各行业的βim系数表示各行业的超额收益相对于市场层面超额收益的对比大小，βim系数是各行业系统性风险的反映。从表4－9的数据中可以看到，通过回归方程计算得出的βim系数都较清楚地体现了各自行业收益数据的行业特点。比如，金融、保险行业是各行业中收益最高，因此金融业拥有超过1的βim风险系数；而交通运输、仓储业由于技术进步和市场竞争的不断加强，行业收益相对较低，所以在样本分析期内交通业的系统性风险系数βim最小，其值只有0．822。

另外，经过适当计量检验，本书发现行业内各波动成分还具有这样两方面事实：

（五）行业内企业波动与行业波动更具相关性

各行业内企业波动与行业波动，企业波动与行业权重系数的相关系数，计算结果都汇总如表4－10所示。

表4－10　行业内企业波动相关系数表

注：表中的交通业指交通运输、仓储业；信息业指信息技术业；金融业指金融、保险业；房产业指房地产业；服务业指社会服务业。

从表4－10的各相关系数能明显看到，各行业的企业波动与自身行业波动具有较强的相关性，相关系数从最低0．4749到最高0．7648。这说明在各行业内企业波动始终受到行业波动较大程度的影响，这种影响是与行业收益的变动紧密联系的。行业的市值权重系数虽然与企业波动呈现反向变动的关系，但其相关程度并非很大。

同时值得指出的是，虽然企业波动与行业波动具有较高程度的相关关系，并且行业波动往往显示出领先于企业波动的变化，但两者经检验却并不存在显著性明显的Granger因果关系。行业权重系数的检验结果也同样表明，行业权重系数并不是（不具普遍性的）企业波动的Granger原因。

（六）行业内企业波动的平稳性也与行业的特点有关

本章第二节对基准样本股的企业波动进行了平稳性检验，证明我国股票市场特质风险是非平稳的时间序列变量，有着较显著的趋势性变动规律。本节对单个行业内的特质风险同样进行单位根检验，检验的结果表明，单个行业的企业波动平稳性与行业本身的特点有着重要联系。表4－11、表4－12显示了对建筑业和交通运输、仓储业企业波动数据的ADF单位根检验结果。这两个行业的特质风险都是一阶单整的时间序列变量，原序列在5%的显著性水平下均不平稳。这里没有表示出来的其他行业的企业波动序列基本属于平稳时间序列。可以看到，平稳性检验的结果表明，企业波动数据的平稳性与股票资产涉及的行业相联系，那么这潜在说明企业波动与所涉行业的发展、变化等情况有关，进而单行业的企业波动还与证券市场给该行业赋予的外部投资环境密切相关。特质风险具有明确的行业特点，这是对单个行业的企业波动进行对比分析后得出的又一结论。

表4－11　建筑业企业波动一阶差分后ADF单位根检验结果

注：检验结果不具有截距项和趋势项。

表4－12　交通运输、仓储业企业波动一阶差分后ADF单位根检验结果

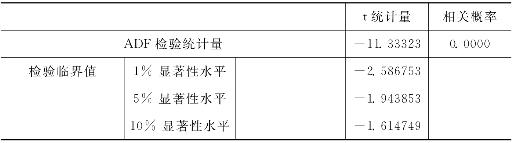
注：检验结果不具有截距项和趋势项。

第三节　股价特质风险的模型描述与波动特征分析

在对股价特质风险进行趋势变动和行业间的对比分析之后，本节对股价特质风险进行适合的模型描述，并针对它所具有的波动特征进行专门的建模分析。

一、股价特质风险变动特征的ARIMA模型描述

本节利用上文已计算得出的基准样本股的特质风险数据进行接下来的实证检验和实证分析。

（一）建立特质风险的ARIMA模型

参考本章第一节（股票资产波动成分的趋势分析）对市场层面波动进行AR（2）模型的建模结果，对特质风险（即分离计算出来的特质风险）可建立ARIMA的回归模型。

本章第一节（股票资产波动成分的趋势分析）对股价特质风险的单位根检验显示FIRM在5%显著性水平下存在单位根，因此需对FIRM进行一阶差分，化为平稳时间序列。令ILFIRM为FIRM的一阶对数差分值，即：

ILFIRMt＝log（FIRMt）－log（FIRMt－1）　　　　　（4－5）

ILFIRM表示了股价特质风险的变化率。再对其进行单位根检验可知，ILFIRM是无趋势项和截距项的零阶单整序列。其偏自相关分析图如图4－11所示。

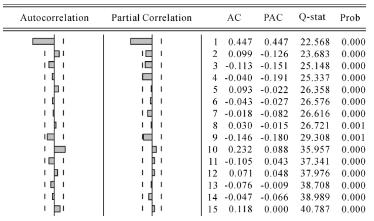
图4－11　序列ILFIRM的自相关—偏自相关分析图

图4－11显示，偏自相关系数和自相关系数在k＝4和k＝1后都很快趋向于0。因此，ARIMA模型可取p＝4或p＝1，q＝1。序列ILFIRM的样本平均数为－0．000992，均值标准误为：

式中为样本方差；n为样本观察值；＾ρk为样本自相关系数；M表示M个显著不为零的样本自相关系数，本书其值为1。根据式（4－6），均值标准误差s计算得到为0．01556。因为样本平均数在±2s的范围内，所以不能拒绝序列ILFIRM均值为零的原假设，不必再对其进行变换。

（二）特质风险ARIMA模型的选择与估计

如果选取ARIMA（4，1，1）作为估计模型，利用EViews6．0计量经济学软件将得到如表4－13所示的方程估计结果。

表4－13　特质风险ARIMA（4，1，1）模型的参数估计与相关检验结果

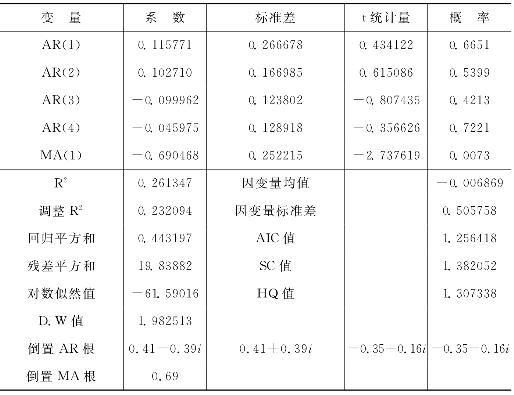
表4－13最下部分的数据表明，回归模型各滞后多项式的倒数根都落在单位圆内，说明ARIMA（4，1，1）模型既平稳，又可逆。

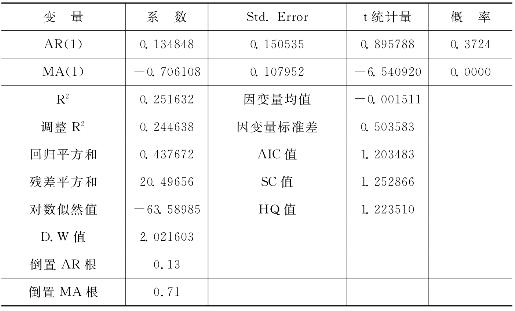
而如果选取ARIMA（1，1，1）作为特质风险的估计模型，同样方法做回归，结果如表4－14所示。

表4－14　特质风险ARIMA（1，1，1）模型的参数估计与相关检验结果

两个不同形式模型的参数估计与相关检验结果分别如表4－15和表4－16所示。

表4－15　两模型的参数估计结果

表4－16　两模型的相关检验结果

从表4－13、表4－14的结果及其对比中，可以看到两种模型均满足ARIMA（p，d，q）过程的平稳条件以及可逆的条件。表4－15、表4－16的结果显示，残差序列相关检验的相伴概率（p－Q）^[6]也都满足了独立性的假定，模型能较好地拟合特质风险原序列。但比较两模型，第二个模型即ARIMA（1，1，1），其AIC和SC标准值都相对来说更小；模型调整后的决定系数（Adjusted　R2）和模型预测的MAIPE值也显示出来，ARIMA（1，1，1）模型的拟合、预测效果更好。因此，从简洁、有效的角度考虑，对特质风险建立的ARIMA（p，d，q）模型应选择ARMA（1，1，1）这种形式。最终股价特质风险ARIMA（1，1，1）模型如图4－12所示，式中B是滞后算子，ut代表模型回归的随机扰动项。方程为：

（1－0．134848B）（1－B）log（FIRMt）＝（1＋0．706108B）ut 　　　　　（4－7）

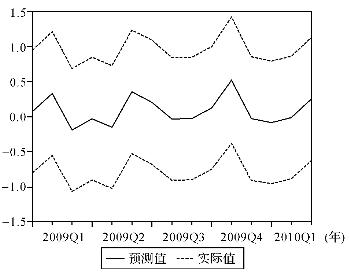
图4－12　特质风险ARIMA（1，1，1）模型预测图

（三）特质风险模型的预测

利用式（4－7）结果，使用特质风险ARIMA（1，1，1）模型可对股价特质风险进行预测效果检验。在将预测期设定为2009年1月至2010年3月后，利用模型回归可得到特质风险的预测图（图4－12）和预测数据如表4－17所示。

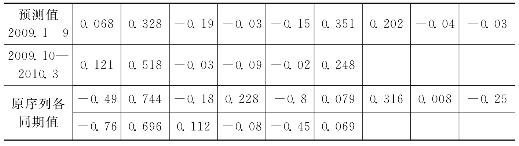
表4－17　特质风险ARIMA（1，1，1）模型预测值结果

从特质风险预测图和预测表的结果来看，ARIMA（1，1，1）模型的预测效果较好，模型实现了较好地拟合股价特质风险的目的。对特质风险的建模结果，其结构与特征也都反映出我国股价特质风险发生波动变化的一些内在规律。

二、股价特质风险的波动特征分析

本章未寻求股价特质风险的解释变量，因此对股价特质风险波动特征的分析是基于特质风险的随机游走（Random　Walk）模型^[7]展开。随机游走模型是股价序列常用的一种特殊单位根过程，最早被K．Pearson和L．Rayleigh于1905年在自然（Nature）杂志第72卷上首次使用。股价特质风险随机游走模型的形式为：

FIRMt＝FIRMt－1＋ut　　　　　（4－8）

（一）特质风险波动的ARCH效应检验

对股价特质风险的随机游走模型进行回归，在回归结果的基础上对模型残差进行基于LM检验的ARCH效应检验。直到q值取9时，χ2检验的相伴概率值为0．0463。如表4－18所示，小于显著性水平5%，拒绝辅助回归方程所有回归系数同时为零的原假设，残差序列存在ARCH效应。而当q值取大于等于10的数时，ARCH效应检验又均不显著，因此综合判断可以认为，特质风险随机游走模型残差序列存在高阶的ARCH效应，即GARCH效应。针对股价特质风险的原序列，可以建立GARCH模型对波动集群性（volatility　clustering）进行描述和分析。

表4－18　特质风险ARCH效应检验结果

（二）特质风险GARCH模型的选择与建立

由于股价特质风险的波动反映了股票资产收益风险的一般特征，即风险越大，预期收益越高，股价波动水平也相应越高。因此对其应采用能利用条件方差反映预期风险的ARCH均值（或称ARCH－M）模型（Engle and Lilien，Robins，1987）。本书经过多轮比较发现如果将条件方差换成对数形式ln），则模型的回归效果会更理想。因此特质风险GARCH模型的均值方程设定为：

另一方面为了表现股票市场对风险冲击具有的非对称反应现象，在GARCH模型的方差等式中加入能反映“杠杆效应”的成分。在诸多描述非对称冲击的GARCH模型中，本书经过反复试验和比较，选择用TARCH模型（Zakoian，1990；Glosten，Jagannathan and Runkle，1993）来设定特质风险的条件方差。本书方差等式的形式为：

式中dt－1是虚拟变量，当ut－1＜0时，dt－1＝1；反之则dt－1＝0。dt－1即是非对称效应项，也称TARCH项。从等式中可以看到，条件方差除由前期的残差平方和条件方差所决定外，不同的消息还会对条件方差造成不同的影响。如当好消息在市场上传播时（ut－1＞0），好消息形成的冲击为α倍的冲击（因为这时dt－1＝0，而dt－1项为零）；而当坏消息传到股票市场中来时，此时形成的冲击为（α＋γ）倍的，很显然这时的冲击和好消息传播时是不对称的。通常认为，只要γ≠0，冲击就一定会形成非对称的冲击效应。而如果γ＞0，坏消息会促使波动程度加大；当γ＜0好消息的传播会更容易引致波动幅度增加。

（三）特质风险的GARCH模型估计及其结果分析

1．股价特质风险TARCH（1，1）－M模型估计结果

利用基于GARCH－M和TARCH模型的GARCH（1，1）模型对股价特质风险进行建模，模型回归的结果如表4－19所示：

表4－19　特质风险TARCH（1，1）－M模型参数估计及检验结果

同时通过对模型回归的残差序列进行ARCH效应的LM检验，可以判定表4－19得到的模型回归结果的残差序列已不存在ARCH效应，特质风险的GARCH（1，1）模型消除了式（4－8）残差序列的条件异方差性。

特质风险GARCH（1，1）模型残差序列的自相关和偏自相关系数已近似为零，相应的Q统计量也不显著，模型回归的效果较为理想。

2．对特质风险GARCH模型的结果分析

以上估计出的结果用方程形式表示为：

均值方程：

条件方差方程：

对数似然值＝575．6445，AIC值＝－10．35717，SC值＝－10．20987。

均值方程中log（GARCH）项的存在，说明我国股价特质风险具有典型的金融资产收益风险特征，这实际上也为资本市场资产定价理论的理论研究提供了实证依据。值得注意的是，与通常金融资产的收益—风险关系不同，股价特质风险的波动与风险因素log（GARCH）之间的变动关系是负向相关的。这说明其中存在的影响机制不再只限定于金融资产风险、收益间的风险溢酬关系（这之间通常具有的是正向变动的关系），隐含地体现出特质风险与信息不确定性、投资者行为效应所可能存在的内在联系。log（GARCH）的风险系数显示出了在它们之间具有的互动影响关系。

在条件方差等式中，系数C（4）＋C（6）＝0．928416＜1，满足GARCH模型参数约束的条件。由于这个ARCH项和GARCH项的系数之和已较为接近于1，这也说明了特质风险波动具有的集群性以及特质风险波动的持续性，这一特性除了符合一般高频金融时间序列的一般特征外，它的变动特点也非常符合投资者行为对股价波动形成的作用影响。

最后，特质风险GARCH（1，1）模型呈现出来的非对称效应也具有很大的启示特征。由于非对称项系数γ＝－0．656＜0，因此特质风险GARCH模型的非对称效应表现出：当好消息在市场上传播时，它形成的冲击是α倍的，比坏消息传播形成的（α＋γ）倍的冲击要来得大。这意味着股价特质风险波动在市场转暖和市场过热时，表现出波动幅度增大；而当市场趋于平淡和趋向“熊市”的时候，又表现出波动平稳的现象。特质风险GARCH模型的这一非对称效应显然要区别于一般股价收益率表现出的“杠杆”非对称效应^[8]。其实正如本书在前面章节做理论分析时获得的结论，股价特质风险促成的股价偏差现象和我国股票市场较强的投机行为密切相关。而从GARCH模型的模型回归中正好能够看到，股票市场上特质风险的波动变化除了具有通常金融时间序列波动集群的特点外，特质风险的变化还受到较明显的投资者行为效应影响。特质风险反向的非对称效应正是自身受到投资者行为效应影响而表现出的综合结果（因为投资者行为效应超过了股价变动的“杠杆效应”，即股票市场的投机效应强过股票市场的投资效应）。

第四节　本章小结

本章通过对股票资产总体波动水平的分解和计算出了3个层面的收益波动成分。使用我国股票市场的数据，对包括股价特质风险在内的3层面波动成分进行了多角度的实证研究。总结这些特质风险的实证分析，可得出这样一些结论。

一、本章的基本结论

第一，在我国股票市场上，股票资产的市场层面波动时间序列表现平稳，呈现出随机波动的特征，并且可以使用一个均值不为零的AR（2）自回归模型描述其波动变化规律。同时，股票资产行业层面波动和特质风险表现为是非平稳时间序列，在行业和企业层面的股价波动变化中存在有趋势变动、波动持续性等特点。

第二，股票资产特质风险是各波动成分中波动幅度最大的风险变化因素，企业层面波动代表的股价特质风险是股票资产价格非随机、非理性波动的主要风险来源。股价特质风险波动与股票资产市场价值及其权重系数表现出反向变动的关系。股价特质风险及其变动还体现出了股票资产所处行业和所属企业的自身特点以及它们产生发展变化的诸多信息。

第三，股价特质风险具有明显的一般金融资产波动集群的特点。股价特质风险与风险因素（如波动特征的条件方差、股市信息等）呈现负向变动的关系。这种负向变动的关系说明了股价特质风险一贯受到股市投机性交易行为的影响，在特质风险与信息不确定性、投资者行为效应之间存在着确实的内在联系。

第四，通过对我国股票市场数据的实证分析，本书发现通过增加持有股票资产数量进行的分散投资并不能明显有效地降低股价特质风险的波动水平。这一现象用传统的CAPM系列模型难以做出合理解释。基于APT模型的思想，本书认为对股票资产企业层面的波动成分（股价特质风险）必须为其寻找新的^[9]、具有解释能力的风险因素。

二、进一步的讨论

依据基础—衍生定价维度的股票资产定价模型，能够促成股价异常波动的因素，要么来自企业未来现金流的变动（可用方差值表示），要么源于资本市场折现率的变动（方差值），再或者是这两者协同变动（两者的协方差）而造成的影响。在这3种风险因素的来源中，无疑尤以企业未来（预期）现金流的变动最能形成股价大幅波动。比如Vuolteenaho（1999）就反对Campbell（1991）提出的是折现率的改变导致了股市波动的观点，Vuolteenaho认为未来（预期）现金流的方差值至少要两倍于折现率的方差值。基于股票上市公司未来现金流的信息不确定性是促成股票资产价格非理性波动，特质风险大幅增加的基本原因。对于信息不确定性，本书认为有如下这样一些影响变量。

第一，股票市场的发展，股票发行的增加，特别是风险投资板块，中小企业板块，投资创业板块等的规模增大会增加股票资产的特质风险波动性。^[10]

第二，股票上市企业杠杆率经营的增加，企业债券市场的相关发展在一定程度上也会增加上市企业发行股票的信息不确定性。^[11]

第三，股票市场信息环境的改善，以及金融创新（特别是金融衍生品市场）的发展能在较大程度上改善股票市场上市公司的信息质量，强化股票市场的市场功能作用（周丹、郭万山，2010），从而能在一定程度上减小股价特质风险的波动水平。^[12]

另外，股票市场的系统性风险以及股票市场的投资者行为构成了股价特质风险动态变化的重要决定因素。

第四，按照CAPM定价模型的框架，股票资产系统性风险性（β值）的变化能够改变资本市场折现率，进而改变股票资产价格。如果系统性风险波动性增强，那么股价资产特质风险的波动性也必然随之增强。Cho and Engle（1999）针对美国市值最大的9只股票组成的资产组合研究得到了这方面的支持证据。

第五，经过本章针对股价特质风险的计算和实证研究，本书认为在我国股票市场上能够体现和显著改变市场投机氛围的恰恰只能够是股票市场的投资者行为。不论是机构投资者数量的增加，还是中小投资者大量的噪声交易，投资者行为在我国股票市场上形成的股价波动影响是显而易见的。Malkiel and Xu（1999）认为机构投资者容易通过“羊群效应”影响股票市场价格波动；Gompers and Metrick（1999）也通过研究发现，机构投资者倾向于保持流动性（相对真正企业股东来说），倾向于大规模交易，这些都较容易增强股票资产的波动性。中小投资者虽然投资额度相对较小，但作为一个投资群体来讲，中小投资者大规模的群体性投机行为，以及他们灵活、频繁的交投方法，仍然对股票资产尤其是股票资产的特质风险造成效果明显的冲击与影响。行为金融理论已从股价异动的角度对投资者行为展开了不断深入的研究，如果转换研究范式，人们将发现甚至是投资者群体的异质性也会通过投资者之间的相互作用影响金融市场的诸多变量（如资本市场折现率、股价特质风险等）。本书第五章将展开对特质风险的投资者行为效应的实证分析。

【注释】

[1]我国股市在2007年10月16日达到历史最高点6124点后，转而迅速步入下行通道，在2008年的大半年时间内股市一路下滑，最终于该年10月28日上证综指跌到1664点，这一点位接近前期历史最低点。这一段股市的大涨、大跌衔接非常紧密，因而形成了我国股市截至日前波幅最为巨大的一波股市震荡，其在理论与实践领域均引起人们不断关注，并产生热议。

[2]扩大样本股和缩小样本股的具体数据计算结果见本书附录。

[3]如果放大置信范围，如将置信范围扩大到10%，行业波动及企业波动也会显示出不存在单位根的结果。但本书为严谨和准确的考虑，因此将置信度限制在较为严格的5%以内。这是鉴于5%以内的置信区间是国内外学术界较常采用的可靠度限定范围。

[4]这其中只是企业波动在2002年到2003年期间波动幅度略有下降，不久在2003年下半年企业波动的变化即完全转入持续上行的通道。

[5]对照趋势分解结果的图形，我们可以发现有多个时间点的股票市场事件能够向我们表明，信息不确定性对行业与企业波动造成的影响。如2005年到2006年初的大牛市；2006年6月7日的股市暴跌；2007年底前的单边上涨行情乃至包括2008年美国次贷危机带给我国股市的冲击等，这些信息不确定性形成的影响都能在波动值分解出的随机变动成分中发现它们的痕迹。

[6]有关残差序列的相关性检验和相伴概率（p－Q）数值的获取，可参见第三章第二节对MKTt进行建模时所作的有关论述。

[7]参看本章第一节对市场波动MKT建立AR（2）模型的对比分析。

[8]金融理论研究发现股票价格变动的特点是：负面冲击往往会比正面影响造成股票价格更大的波动。这当中解释的原因之一是，较低的股价会减少股东的所有者权益，股价大幅下跌就增大了公司经营的杠杆作用，这样必然提高了持有对应股票资产所面临的风险。

[9]除去超额市场收益、规模因子和B／M比值之外的有关解释因素，如本书认为的信息不确定性、投资者行为效应等。

[10]具体相关方面的研究可参看Gertner，Scharfstein and Stein（1994）、Stein（1997）、Morck，Yeung and Yu（2000）等的论述。

[11]可参见Black（1976）、Christie（1981）对企业杠杆经营及其对股票收益影响的论证。

[12]Shiller（1981）、LeRoy and Porter（1981）、West（1988）、Conrad（1989）、Skinner（1989）、Kumar，Sarin and Shastri（1998）在市场信息质量和金融衍生市场对股票市场功能影响这些方面做了有代表性的研究。