单因子校准模型

六、单因子校准模型

单因子的均衡模型中,短期利率具有单一随机变量,而收益曲线是单一变量的函数,当用二叉树进行数值计算时比较简单,因此,得到广泛的应用。但是均衡模型并不能与实际的收益曲线相吻合,影响了固定收益证券定价的有效性。通过在模型中引入时间依赖的参数,使模型与收益曲线相吻合。这里以带时间依赖漂移项的Vasiek模型为例。

(一)带时间依赖漂移项的Vasiek模型

Vasicek(1977)模型中的短期利率满足下列方程:

Wt为自然测度下的维纳过程,在风险中性测度Q条件下,Vasicek(1977)模型中的短期利率满足下列方程:

W_tQ风险中性测度Q下的维纳过程,λ是风险的市场价格,θ=μ-λσ/k是风险中性均值,固定收益证券的价格只依赖于Q测度下r_t的分布,因此下面我们不关心在自然概率下短期利率的过程。

一般情况下,(3.2)式中的短期利率过程并不能与实际的收益曲线相吻合,这里用时间依赖均值θ(t)扩展该模型:

随机微分方程(3.2)式的解可表示为:

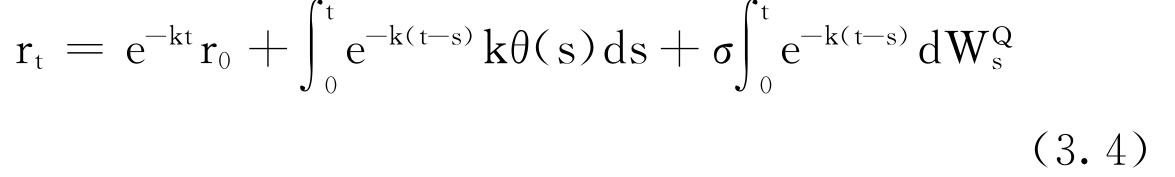
定义m(t)和x_t以下:

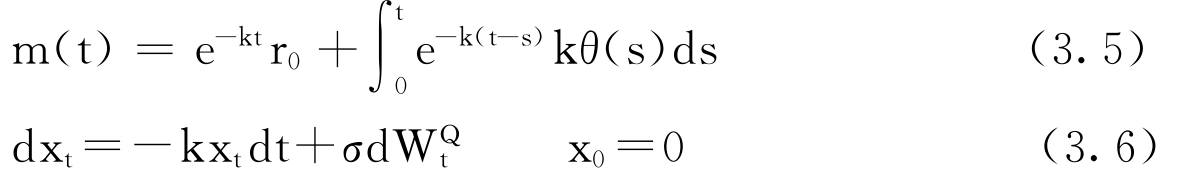
可以把r_t重写为:

(3.3)式与(3.6)式是等价的,无套利机会暗示T时到期的零息债券在t时的价格由风险中性概率的期望值给出:

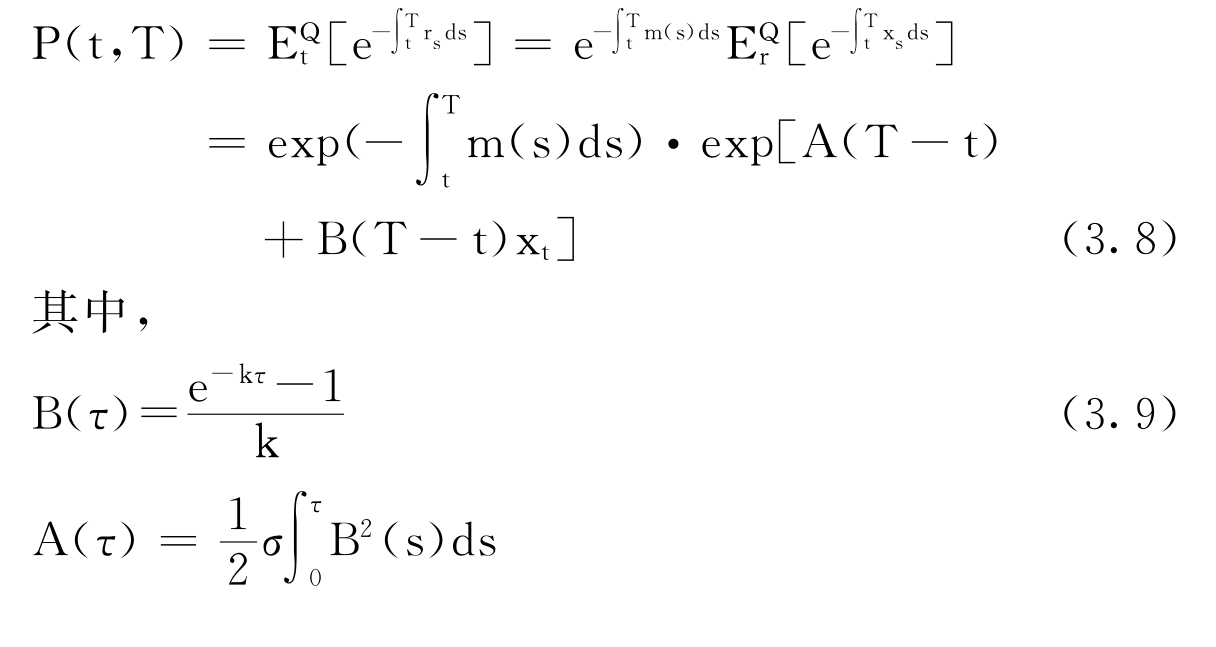
注意(3.8)式中的P(t,T)表示为一个决定性要素和Q测度下具有零均值的普通Vasicek模型的债券价格的乘积。

(二)带时间依赖参数的校准

为了使利率过程与收益曲线相吻合,把贴现函数表示如下:

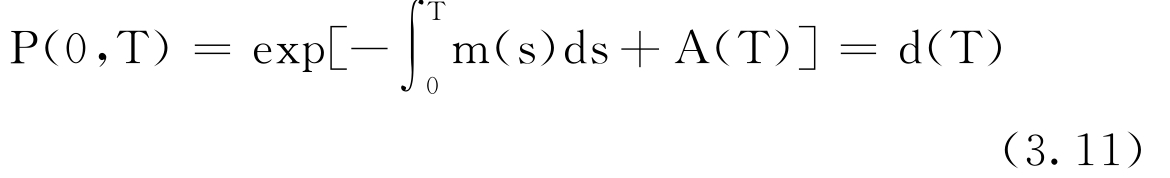
由上式有:两边分别对T求导,得

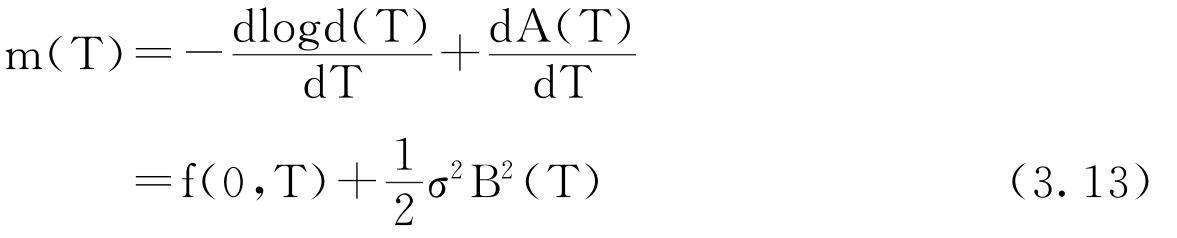
这意味着m(T)可以由初始的远期利率曲线f(0,T)得到,而参数k和σ,在计算之前必须先确定,原则上可以用市场价格(例如利率上限)反推出。

为了求出θ(t)的表达式,(3.5)式对t求导得:

　　　　　　　=kθ(t)-km(t)　　　　　　　　　　　(3.14)

利用这个结果,和(3.13)式中定义的m(t)得到:

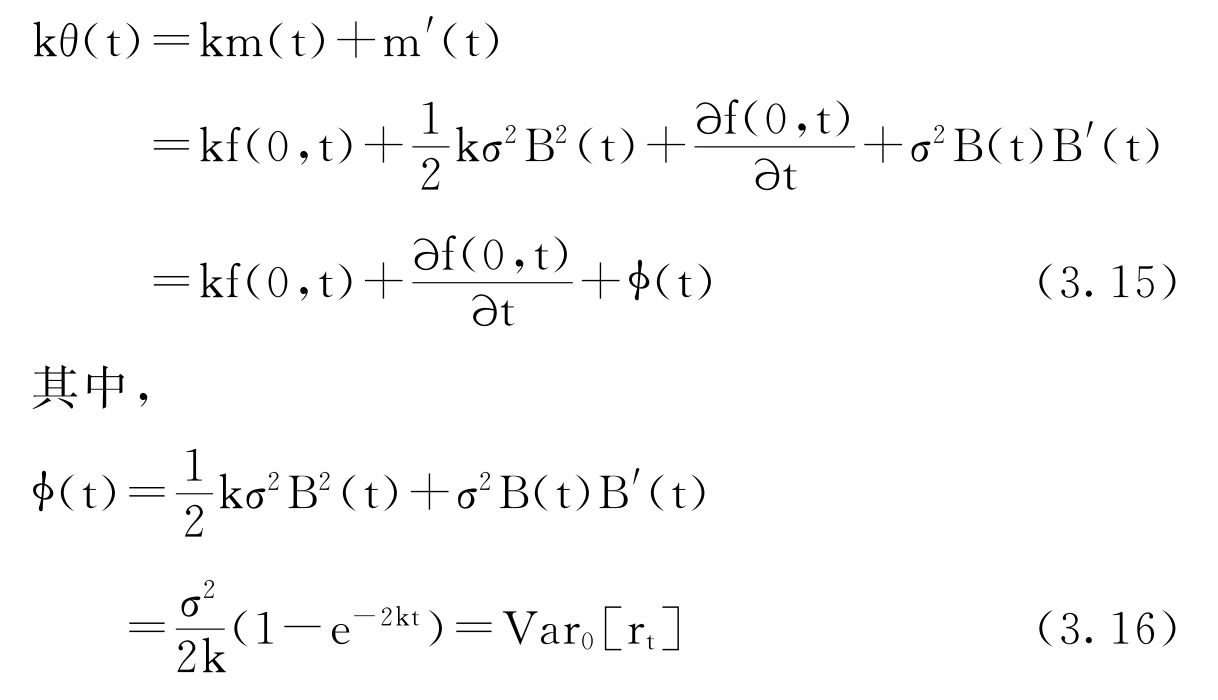
是给定r₀下的条件方差,有了上面的分析,可以把r_t的随机微分方程重新写为:

　　　　　　　　　　　　　　　　　　　　　　　(3.17)

这说明时间依赖参数由初始收益曲线得到,或者更准确地说,是由远期利率曲线f(0,t)得到。

(三)零息债券的价格

由(3.8)式,t时债券价格为:

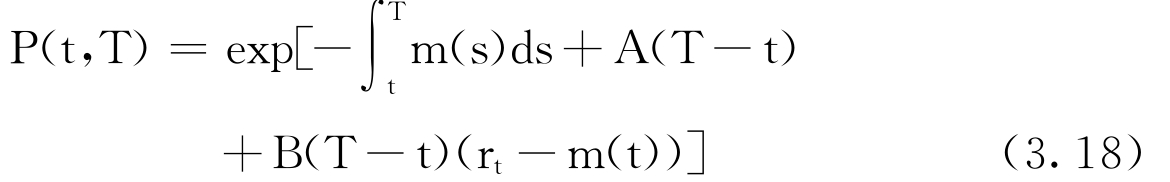
这里m(s),t≤s≤T,由初始的期限结构校准得到,下面通过整理使(3.18)式更容易理解,注意到T时到期债券的远期价格:

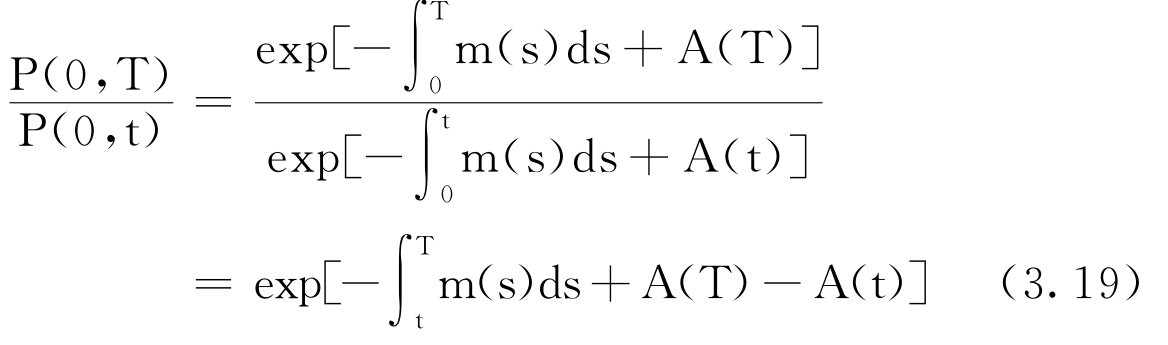
结合(3.18)和(3.19)式,得到

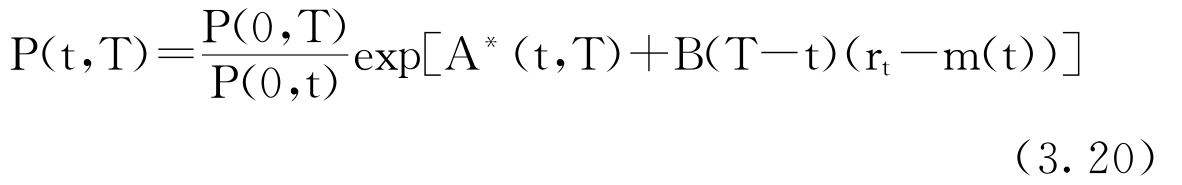
这里A^∗(t,T)=A(T-t)+A(t)-A(T),整理得到A^∗(t,T)的公式:

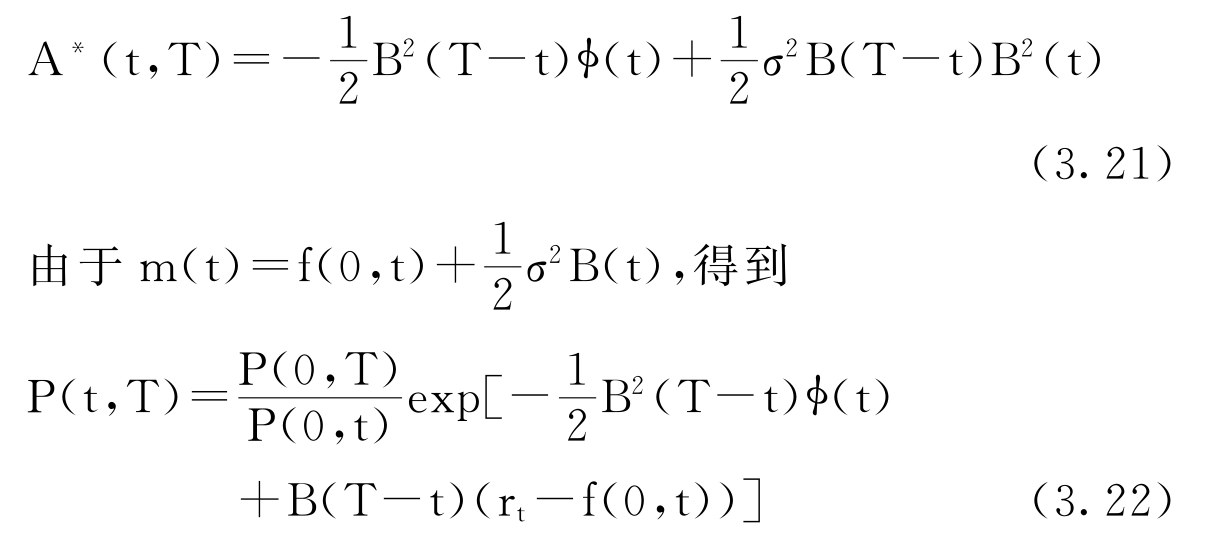
这说明P(t,T)只与远期利率曲线f(0,t)有关,实际上,校准模型可以通过二叉数或三叉数进行数值计算。