【摘要】：令由式定义的P(t,T)为T时到期的无违约风险零息债券在t时的价格,选择P(t,T)为计价单位,以P(t,T)定义的公司资产名义价值为:根据Gemam的结论,必然存在远期中性测度QT,使得AT过程为鞅过程,则公司资产名义价值在QT测度下可表示为以下偏微分方程:其中zt1和zt2为满足关系式dzt1dzt2=ρdt的标准维纳过程,NT为具有强度为h的泊松过程,Y为QT测度下的跳跃幅度。强度h和平均跳跃幅度k可通过市场数据估计。②强度函数h通过牛顿方法应用信用差价数据估计。
三、公司债务定价
假设公司发行两种权益,单一公司债券与股票。下面在该假设条件下,得到公司债券定价的封闭解表达式。
令由(1)式定义的P(t,T)为T时到期的无违约风险零息债券在t时的价格,选择P(t,T)为计价单位,以P(t,T)定义的公司资产名义价值为:
根据Gemam(1995)的结论,必然存在远期中性测度QT,使得AT(t)过程为鞅过程,则公司资产名义价值在QT(t)测度下可表示为以下偏微分方程:
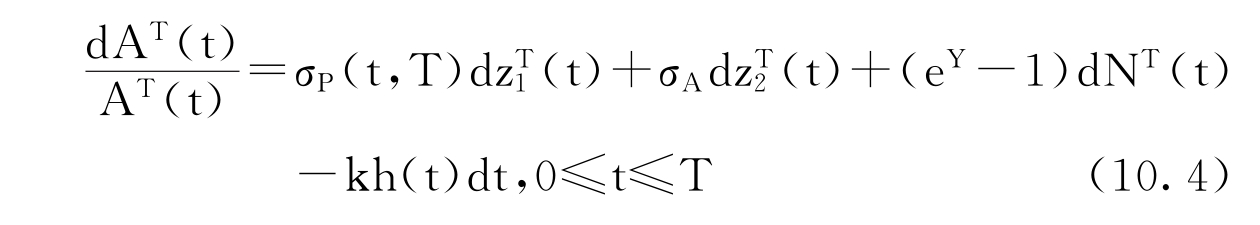
其中zt1(t)和zt2(t)为满足关系式dzt1(t)dzt2(t)=ρdt的标准维纳过程,NT(t)为具有强度为h(t)的泊松过程,Y为QT测度下的跳跃幅度。强度h(t)和平均跳跃幅度k可通过市场数据估计。
令zT(t)为QT测度下的另一标准维纳过程,并且定义:
这里Yi为相互独立,且与Y具有相同的分布。
在NT(t)=n条件下,long{AT(t)/AT(0)}为正态分布,具有均值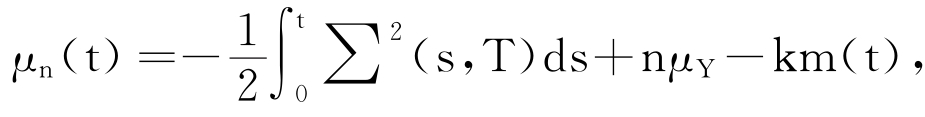
,方差
NT(t)的累积强度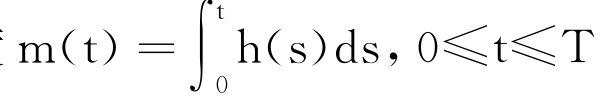
,表示直到t时在QT测度下的跳跃次数,即m(t)=ET[NT(t)]。
假设到期日时,当公司不能支付承诺本金F时,违约发生,此时,债券持有者立即接管公司资产,而股票持有者什么也得不到,股票持有者在到期日的支付函数为:
根据Geman(1995),T时到期的公司贴现债券在t时的价格为:
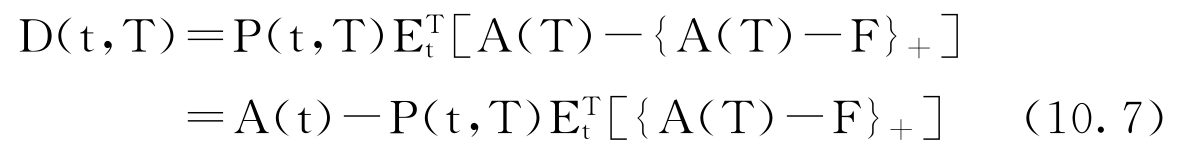
扩展Zhou(1997)跳—扩散过程中的结论,得到下面的引理。
引理
1公司贴现债券的价值
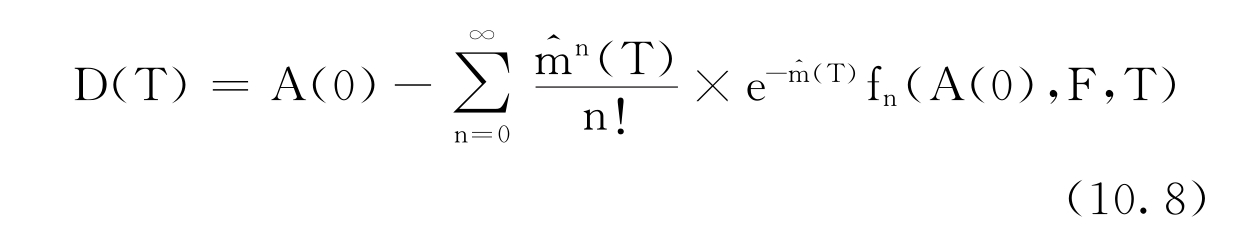
信用差价的期限结构
Φ(·)表示标准正态分布函数。
参数估计分两部分:①扩散波动率σA和跳跃幅度波动率σY通过一般的似然方法由股票收益率的历史数据得到。②强度函数h(t)通过牛顿方法应用信用差价数据估计。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
