5 我国股票市场相依性的实证研究
20世纪80年代以来,交易技术的提高使得市场信息可以短时间内在不同股票市场之间迅速传递,不同资本市场之间报酬与风险等因素相互交织,全球资本市场一体化过程呈现不可阻挡之势。全球资本市场一体化背景下,中国股市开放度日益加强,与世界资本市场越来越紧密。此时研究中国股票市场与其他股票市场的联动性就具有非常现实的意义。
股票市场的联动性可以分为两大类,一是全球股票市场的联动性,以美国股票市场对全球股市的影响最为典型,如2007年美国次贷危机所导致的全球股市暴跌。二是某个区域内股票市场之间的联动性,可以香港股市和中国内地股市的联动性为例。自从亚洲金融危机后,Hyuk Choe等(1998)等发现是韩国本地的投资者在金融危机前先抽出资金(在外国投资者出手之前)。韩国的投资者比外国投资者可能知道更多的当地信息,他们能够对点滴的信息反应相当敏感。该研究因此认为韩国金融危机的真实起源在于国内。该研究开创了股市联动的先例。
学术界对于股市联动内在机制的讨论,从概念上可分为两类。第一类侧重于将股市关联性归因于实体经济的联系,Calvo,Reinhart(1996)称其为“经济基础说”。经济全球化使各国在实体经济层面更依赖于其他国家,金融全球化减少了跨国套利的成本(例如法律约束及交易成本)。这些原因将各国股市紧密地联系在一起。例如,国际利率提高、国际资本供应的紧缩以及国际商品需求的减少会同时拖累数个国家的发展,这些国家的资产价格也因此表现出相同的运动趋势。第二类被称为“市场传染假说”,认为股市关联性不能完全由可观察的宏观经济联系解释,而应该从投资者心理行为上寻找原因。当一国股市受到负面冲击时,负面影响会如疾病传染一样扩散到国际市场,导致危机时期各国股市关联性的增强。Rigobon(1998)根据学习模型提出市场冲击的传导源于投资者对市场的再评估。例如,当一国银行受到金融危机的冲击后,投资者会重新评估其他国家银行的稳定性,修正他们对于其他国家发生危机的概率判断并调整对该国市场的估值。
在金融市场上,金融风险是由金融资产价格的波动引起的,价格的变动反映了市场对新信息的反应;成交量作为市场交易中供需情况的具体表现,反映了投资者对新信息认同的差异程度;波动性则反映了价格变动的剧烈程度。对股票市场收益、收益波动以及成交量之间关系的研究是了解金融市场微观结构的一个途径,也是研究套利机会或者说市场有效性、揭示价格波动产生的根源的重要手段。因此,本书拟采用以Copula为主的研究方法,通过对不同市场之间的交易量、价格和波动性的关系来实证研究我国股票市场的相关性问题。
5. 1 我国股票市场信息传递的非线性G r anger检验
5.1.1 引言
市场一体化是指打破市场之间的壁垒,建立统一经济空间,以实现资源在整个市场范围内的最优配置。其最终表现为同质的市场交易品种的价格在不同市场间是均衡的,同一市场交易品种的价格或者通过风险调整后的收益在不同市场中是相同的,不存在跨市套利机会。相对于市场一体化而言,股票市场分割是指市场间交易机制、投资者构成的差异导致同质的股票在价格、收益率、风险等方面呈现出较大的差异。2001年2月19日前中国A股、B股市场的投资者限制,就是一种壁垒。尽管两个市场存在非常大的价差,但由于两个市场的分割而无法实施套利行为。
股票市场分割是很多国家都存在的现象,所以国外从20世纪70年代就开始了市场分割的研究。对于市场分割的界定,最初的方法是通过分析不同市场的股价收益率是否受到相同的因素驱动来进行论证。如果两个市场资产的定价基于统一的因素,如CAPM模型的系统风险因素或多因素资产定价模型的各风险因素,则认为市场是一体化的。否则,就认为两个市场是分割的。邹功达、陈浪南(2002)也基于CAPM模型验证了上海和深圳的A股和B股市场截至2000年6月具有较强的一体化程度。然而,由于许多市场不只受到一个风险因素的驱动,近年来大量文献的研究如Kandel与Stambaugh(1989)和Shanken(1996)都支持CAPM模型不成立的结论。而多因素模型中的因素选取又有主观性的缺陷,所以基于资产定价模型的市场分割的界定在实证分析中存在一定的局限性。
正是由于上述方法的局限性,出现了从两个市场之间的信息流动来间接研究市场分割的另一种方法。信息流动情况可以更直观地反应市场分割的效果。如果两个市场是完全一体化的,那么市场之间的信息流动将不存在壁垒,表现为两个市场价格的互动,两个市场之间不存在套利机会。当市场为局部分割时,信息则从一个市场流向另一个市场,表现为一个市场的价格引导另一市场的价格,投资者可能从中获取套利。市场分割的极端情况是两个市场之间的信息互不流动,表现为两个市场价格的相对独立,不存在一个市场的价格引导另一市场价格的情形,投资者无法兑现明显存在的套利机会。
从2001年2月19日证监会宣布B股向境内居民开放,2003年5月23日证监会批准第一家合格境外机构投资者(QFII)瑞士银行(UBSAG),到2008年6月底,证监会共批准了58只QFII,合格境内机构投资者(QDII)基金发行数量也增加至九只,解决A、B股市场的分割,实现两个市场的一体化已成为发展和规范我国证券市场的一个重要课题。中国股票市场A股和B股之间的信息流动问题,已有许多学者做了一些研究,其中Chakravarty,Sarkar 和Wu(1998)发现A股收益引导B股收益,而不是相反。但是Chui和Kwok(1998)发现完全相反的结果。其研究结论是B股市场的收益率对A股收益率有先导作用,即信息是从B股市场流向A股市场。他们同时指出这种现象的原因是B股市场的大机构投资者所具有的专业经验优势使得其比A股投资者获取新信息的速度更快。Sjoo和Zhang(2000)通过对1993年6月到1997年6月同时发行A股和B股的41家股票收益率的引导关系的研究,其结论表明:在规模更大、流动性也更好的上海证券交易所,信息的流动是从B股市场流向A股市场,而深圳证券交易所的结论比较模糊。Fung等(2000)利用1993年至1997年样本的实证研究认为,中国A、B股两个市场间并不存在较强的相关性,而是相对分割和独立的。Chen,Lee和Rui(2001)的结论也表明两个市场之间基本上不存在信息流动,两个市场的分割程度比较严重。由此可见,这些研究结果存在很大的差别,许多甚至是矛盾的。这一方面是由于采用的数据样本区间或实证方法不同,另一方面更深层次的原因可能是这些研究都是基于日度收益数据进行。如果股价对信息的调整速度极为迅速,那么不同市场之间的动态关系就不能通过日度数据检测。因此非常有必要采用高频数据进行分析。另外,基于日度收益数据进行研究也忽略了顺序流的信息内容,而Hasbrouck(1991)已经显示该信息对后续收益有显著的预测能力。因此本书拟根据信息经济学理论,采用高频数据建立相应的模型对我国A、B股市场之间的量价信息传递特征进行全面的研究。
5.1.2 线性和非线性Granger因果检验
价格和交易量是证券市场的基础变量,研究价格和交易量之间的关系也一直是诸多研究人员的兴趣所在。长期的研究发现用以解释股价和交易量之间正向关系的理论模型有四大类,分别为信息理论模型、交易理论模型、信息非对称模型和理念分散模型,其中信息理论模型得到国外市场研究更多地支持。信息理论模型具体又主要包括三类:混合分布假设模型、信息顺序到达模型和噪声交易模型。
在实证研究方面,由于Granger(1980)认为真实世界几乎可以肯定地是非线性的,单变量和多变量非线性模型才是拟合和建模的正确方法。由此Hiemstra和Jones(1994)利用非线性Granger因果检验的非参数方法,得到NYSE的交易量和市场收益之间存在双向的非线性因果关系。正如赵留彦、王一鸣(2003)指出,由于信息传递速度很快,使用日内高频数据考察价量关系可能会另外得出有益的结论。因此本节拟采用高频数据全面考察我国股票市场中交易量和价格之间的动态关系,并对检验的结果进行分析。本节的研究方法是研究量价引导关系常用的线性和非线性Granger因果检验方法,但是由于对高频数据的波动率建模一直存在异议,所以本节不以张永东、黎荣舟(2003)采用的波动率和交易量变化率为研究变量而是以日内收益和交易量为研究变量,研究的市场对象包括上海和深圳A、B股市场,也比该文更为全面。
1)数据选取和分析。本节的样本期是2006年5月19日到2007年9月28日,选取的数据包括上证A股综合指数、上证B股综合指数、深圳A股综合指数、深圳B股综合指数在样本期交易日的每5分钟指数价格序列以及对应的交易量序列。本书的数据来源是从交易所取得。价格和交易量序列分别用P和V表示,其中V为取对数后的交易量。由于股票市场高频数据分布在日内呈现典型的W形状,所以舍去每天上下午开盘和收盘时的15分钟数据,即每天每个序列由48个数据舍为36个数据,另舍去极少数缺失的数据,实际样本数为13968组。
由于对非平稳时间序列数据进行回归分析可能产生伪回归,Granger因果检验要求时间序列是平稳的,因此在设定模型形式之前,首先应对各序列进行平稳性检验。通过公式Rt= 100×ln(Pt/ Pt-1)可得到收益序列R。ADF检验表明:序列P存在单位根,序列R和V都是平稳序列。
2)线性Granger因果检验。Granger(1969)提出了因果关系检验的基本框架。设{ xt}和{ yt}是两个平稳的时间序列,![]() = (xt-lx,xt-lx+1,…xt-1)为xt的lx阶滞后向量,
= (xt-lx,xt-lx+1,…xt-1)为xt的lx阶滞后向量,![]() =(yt-ly,yt-ly+1,…yt-1)为yt的ly阶滞后向量,则xt的条件概率分布可表示为
=(yt-ly,yt-ly+1,…yt-1)为yt的ly阶滞后向量,则xt的条件概率分布可表示为![]() 。当滞后阶数lx和ly给定时,如果
。当滞后阶数lx和ly给定时,如果![]() ,=
,=![]() ,则称变量y严格地不能Granger引起x。如果等式不成立,则意味着过去的y值有助于预测现在的x值,那么就称y严格地是x的Granger原因。
,则称变量y严格地不能Granger引起x。如果等式不成立,则意味着过去的y值有助于预测现在的x值,那么就称y严格地是x的Granger原因。
根据Granger因果关系的定义,两个变量之间的线性Granger因果检验模型可通过如下VAR模型给出:
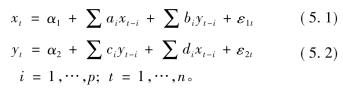
其中:α1、α2分别为x、y的截距项,ai、bi、ci和di为各滞后项相应的系数,ε1t和ε2t为白噪声且相互独立。
通过检验系数是否显著异于零可以考察某一变量对另一变量是否有显著的线性预测能力。若bi显著异于0,认为存在y到x的单向引导关系。同理若di显著异于0,则认为存在x到y的单向引导关系。若bi和di均显著异于0,则存在双向的引导关系。检验之前需先通过AIC法则确定VAR模型的滞后阶。检验结果如表5-1。
表5-1 中国股市量价线性Granger因果关系检验
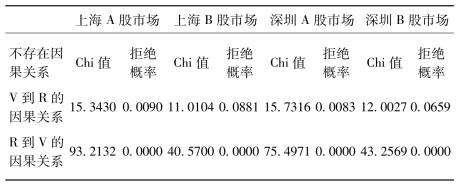
由表5-1可知,在10%的显著性水平下,上海A股市场、上海B股市场、深圳A股市场和深圳B股市场既存在交易量到收益的线性引导关系,又存在收益到交易量的线性引导关系。也就是说各市场量价之间均有双向的线性Granger因果关系;但是将显著性水平限制为5%时,上海A股市场、深圳A股市场量价之间仍有双向的线性Granger因果关系,而上海B股市场、深圳B股市场只有收益到交易量的单向线性Granger因果关系,并不存在交易量到收益的线性Granger因果关系。
3)非线性Granger因果检验。线性Granger因果检验的前提是变量之间是线性函数关系,此时才能用最小均方误差作为评价新增预测能力的标准。该检验发现线性因果关系的能力很强,但是发现非线性因果的能力非常弱。如果变量之间是非线性相关关系,应该在剔除变量之间可能存在的线性因果关系的影响之后,采用Baek和Brock(1992)方法来检验给定时序之间的非线性动态相关的存在性。该方法是基于时序短期相关关系的非参数估计。其基本原理可表述为:
设{ xt}和{ yt}是两个严格平稳、弱依赖的时间序列,xt和yt的滞后向量表示同前![]() 是xt和yt的m阶超前向量。对给定的m,lx,ly≥1和e>0,若
是xt和yt的m阶超前向量。对给定的m,lx,ly≥1和e>0,若

则说y不是x的(严格的)Granger非线性原因。其中的Pr表示概率,‖‖表示最大范数。上述等式的含义是,设定条件一为xt相应的lx阶滞后向量和yt相应的ly阶滞后向量都在距离e内;条件二为xt相应的lx阶滞后向量的距离小于e。在这两种条件下,xt的任意两个m阶超前向量的距离小于e的概率相等。
以上检验要求方程(5.1)、(5.2)的标准化残差为iid。Hiemstra和Jones(1994)指出此条件很难满足,因此提出修正检验,其特点是放松了检验序列为iid的假设,允许VAR模型的残差序列有较弱的或短期的相关。此时上(5.3)式也可以具体的表示为:
![]()
其中C1、C2、C3和C4分别为联合概率的卷积分估计量:
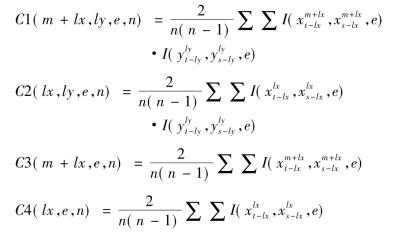
其中t<s,t,s=max(lx,ly)+ 1,…,T-m+ 1,n= T+ 1-mmax(lx,ly)。I(Z1,Z2,e)表示核,当Z1和Z2因子在极大范数距离内时为1,其他时候均为0。在上述假定下,如果y不能严格非线性Granger引起x,则有下式:
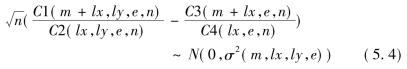
根据Hiemstra和Jones的建议,对于各种情形,参数分别选定m=1,lx= ly,滞后阶为从1至6。所有的检验都应用于标准化序列,标准化序列的标准差σ都等于1,从而也就可以采用一个共同的标度参数e,通常选定e=1.5σ。检验结果见表5-2。
表5-2 中国股市量价非线性Granger因果关系检验
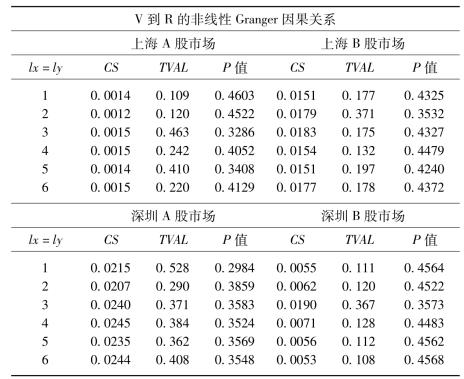
续表
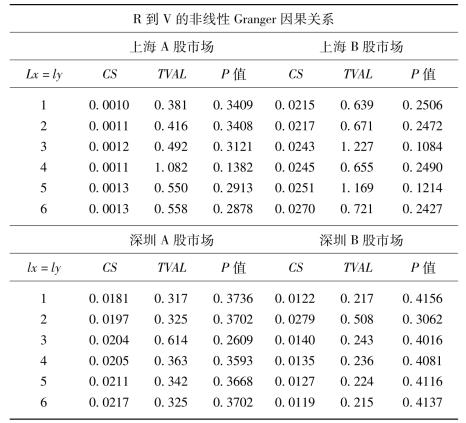
注:CS表示式(5.3)的两个条件概率之差,TVAL为标准化的统计量,P值表示该统计量的右侧单边概率。
对VAR过滤后的残差进行非线性Granger因果关系检验发现各市场的检验结果比较统一。在10%的显著性水平下,上海A股市场、上海B股市场、深圳A股市场和深圳B股市场既不存在交易量到收益的非线性引导关系,也不存在收益到交易量的非线性引导关系。也就是说各市场量价之间均不存在非线性Granger因果关系。因此采用高频数据的研究结果表明在10%的显著性水平下,各市场量价之间仅存在双向的线性Granger因果关系。这个结论和张永东、黎荣舟(2003)相同。
由上可知,采用高频数据与采用每日、每周的数据进行量价关系研究的结果完全不同。采用日度、周度数据的研究得到的结果有些是矛盾的,一个可能的原因是这些研究都是基于日度、周度数据而进行。如果股价对信息的调整速度极为迅速,那么不同变量之间的动态关系就不能通过日度、周度数据检测,此时采用高频数据进行动态关系的研究很可能是一个正确的选择。
5.1.3 基于高频数据的我国股市信息传递研究
1)数据处理和模型设计。
(1)样本数据的选取、说明和分析。为了检查A、B股市场之间的交易量和价格变化之间的动态关系,一个理想的办法是考察同时在A、B股市场上市的单个公司的A、B股收益和交易量之间的关系,然而由于B股市场交易不活跃,个股在许多交易日里价格不变或者没有交易,而且个股价格含有过多的噪音成分。而采用A股和B股市场的指数收益是一种简便易行的办法,由于绝大多数B股公司同时发行A股,这种方法不甚精确的可能性降低,因此本书采用指数收益来代替个股收益来考察A、B股市场之间的量价信息传递特征。需要说明的是,本书没有将两个市场的波动率纳入模型,一是因为高频数据的波动率建模(拟合和预测)非常复杂,二是因为诸多研究证明波动率和交易量之间是比较明显的非线性关系。
本节的样本期、选取的数据和5.1.2节完全相同,仅交易量序列改为LNV表示,LNV为取对数后的交易量。由于对非平稳时间序列数据进行回归分析可能产生伪回归,因此在设定模型形式和对模型进行估计之前,首先应对各序列进行平稳性检验。通过公式Rt= 100×ln(Pt/Pt-1)可得到收益序列R。ADF检验表明:序列P存在单位根,序列R和LNV都是平稳序列。
(2)方法与模型。对相互联系的多变量进行预测和分析随机扰动对变量系统的动态冲击,常用的模型是VAR模型,但是VAR模型没有给出变量之间当期相关关系的确切形式。而SVAR模型则在模型中包含了变量之间的当期关系,根据经济理论对参数空间施加一定的约束以使得当期新息冲击可以传递并影响其他变量的当期和未来变化。因此本书根据上一小节的结论建立SVAR模型,通过脉冲响应函数检查变量之间的动态关系,并由此探讨我国在采取对国内投资者开放B股市场以及实施QFII制度后A、B股市场分割或一体化的程度。
与一个包含m个内生变量的p阶VAR模型对应的SVAR模型为:
![]()
本书的Y为一个四维向量,各变量依次为A股市场的收益率、成交量和B股市场的收益率、成交量,分别用RA、LNVA、RB 和LNVB表示。其中B矩阵体现了变量之间当期的作用和反馈关系。B矩阵的主对角线上的元素为1,非主对角线上的元素bij表示第j个变量变化第i个变量的当期直接影响。根据金融理论,对A、B股市场的量价当期相互关系做出如下假设:1)一般来说,在某一个市场中,成交量是价格趋势的先行指标,是股价变化的原动力。由此根据Hasbrouck(1991)假设交易量到收益有同期和滞后的因果关系,反过来收益到交易量只有滞后的因果关系。所以b21=0,b43=0。2)跨市场同种变量之间关系尤其是同期关系和不同种变量之间相比通常来说要强许多。所以可以认为跨市场同种变量之间有同期影响关系,跨市场且变量为不同种变量之间的同期影响为0。举例来说,A股市场的收益只会对B股市场的同期收益产生影响,而不会对B股市场的同期交易量产生影响,反之亦然。所以b41=0,b32=0,b23= 0,b14= 0。基于以上6个合理的假设,本书设定的B矩阵为:

2)模型的估计及结果分析。
(1)SVAR模型中当期相关矩阵的估计及结果分析。分别对上海深圳A、B股市场的量价关系建立SVAR模型,通过AIC准则确定模型的滞后阶为5,矩阵B的估计结果见表5-3。由于对上海和深圳两地进行研究的结论非常相似,所以下面只以上海A、B股市场的估计结果进行详细的分析。该市场的估计B矩阵列于设定B矩阵的右侧。可以肯定的是,本书的结果和唐齐鸣、刘亚清(2007)由于采用的数据频率不同而明显有所不同。
表5-3 上海深圳A、B股市场量价关系的SVAR模型估计结果

首先考虑单个的A股市场或B股市场的同期量价关系。在5%的显著性水平下,b12、b34显著异于零,这说明A股(B股)市场的量价之间有交易量到收益的当期因果关系,该市场交易量对当期收益的有明显的信息传递,成交量新息的冲击会对该市场的当期收益产生影响。不同的是,A股市场交易量对当期收益的信息传递为正,而B股市场相应的信息传递为负。这也证明了成交量是股价趋势的先行指标。这个结果和Darrat等(2003)一样,验证了信息顺序到达模型。
然后考虑A、B股市场之间的当期量价信息传递。①由于b13,b31的高度显著,说明A股市场和B股市场之间收益有明显的同期相关关系,A股市场的收益的信息会有效的传递到B股市场,反之亦然。同时,b31(3.121791)的绝对值明显大于b13(-1.478373)的绝对值,说明A股市场对B股市场的同期收益信息传递效应显著强于相反的方向。②b24,b42的高度显著,说明A、B股市场之间的交易量信息也同期有效在两个市场之间传递。b42(5.557262)的绝对值明显大于b24(-3.065331)的绝对值,说明A股市场对B股市场的同期交易量信息传递效应明显强于相反的方向。总体来说,可以确定A、B市场之间同期信息流是双向传导的,但是同期信息传递占优的方向仍然是从A股市场到B股市场。这也符合我国B股市场功能缺失的现实。在2001年以后,中国B股市场已经基本没有新的筹资活动,中国设立B股市场最基础也是最重要的筹资功能基本上丧失殆尽,B股市场陷入了功能缺失的困境。B股的涨跌完全随同于A股市场的涨跌,B股市场已经边缘化。
(2)脉冲响应函数。除了分析变量之间的同期因果关系之外,SVAR模型还可以分析当一个误差项发生变化或者说模型受到某种冲击对系统的动态影响,即采用脉冲响应函数方法发现A、B股市场信息的传递途径和特点,尤其是收益、成交量之间相互因果关系。
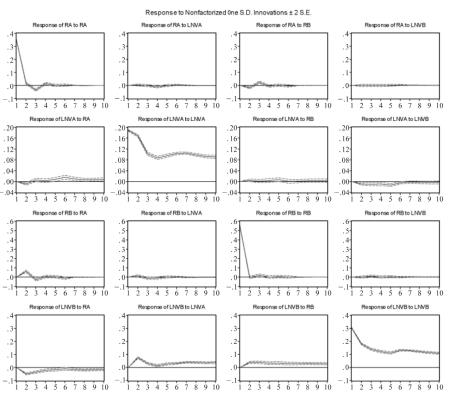
图5-1 上海A、B股市场量价关系的脉冲响应函数图
同样只以上海A、B股市场的脉冲响应函数进行详细的分析。图5-1的16个小图分别代表上海A、B股市场量价之间给一个变量一个单位标准偏差的正冲击,得到其他变量的脉冲响应函数图。反应也用标准偏差单位衡量。图中实线表示对相应冲击的脉冲响应函数,虚线表示正负两倍标准差偏离带。为分析方便,本书将16个图以类似矩阵的形式从左至右、从上到下依次称为图11,图12,…图44。
首先考虑单个的A股市场或B股市场的脉冲响应函数。①从图11可以看出A股市场的收益新息对该市场收益冲击持续的时间较短。在5分钟之内首先引起的同市场收益冲击效应是明显的正效应,然后在15分钟之内迅速波动衰减为接近于0。说明这一冲击具有明显的正向促进作用。从图33看出B股市场的情况与此非常相似。②从图22可以看出,A股市场的交易量新息对该市场交易量冲击持续的时间较长。在15分钟之内引起的同市场交易量冲击效应是明显的正效应,但在15分钟以后基本稳定为0.08,说明这一冲击具有显著的正向促进作用和较长的持续效应。从图44看出B股市场也是如此。因此可以说,不管是A股市场还是B股市场,相对收益的短期自相关来说,交易量则是长期自相关的。③从图12和图21可以看出,A市场的交易量新息对该市场的收益的冲击很小、几乎为零,成交量的冲击几乎不对该市场的收益产生影响。A市场的收益新息对A市场的交易量的冲击也较小(0.01),但是有比较明显的正影响。从图34和图43看出B股市场也是如此,并且B股市场的收益新息对该市场交易量的冲击明显为正(0.03),说明该市场价量反应要强烈的多。本书通过检验得到两个市场均只有收益到交易量的Granger引导关系而没有反向的因果关系(因节省篇幅未列出),在这里也得到了证明。
然后考虑A、B股市场之间的脉冲信息传递。①从图31和图13可以看出,A股市场的收益新息对B股市场的收益有明显的冲击效应,进一步说明A股市场的收益的信息会有效的传递到B股市场然。反之,B股市场的收益新息对A股市场的收益冲击相对来说非常微弱。这个从累计冲击反应看得更加明显。②从图42和图24可以看出,A股市场的交易量新息对B股市场的交易量有明显为正的冲击效应,而B股市场的交易量新息对A股市场的交易量的脉冲反应比较微弱。这再一次说明不管是从收益的信息传递,还是从交易量的信息传递来说,虽然A、B市场之间有双向传递的信息流,但是信息传递的途径仍然是主要从A股市场到B股市场,信息主要是在A股市场发现。
5.1.4 结论
本书首先采用高频数据检验了上海和深圳各股市价格和交易量之间的线性和非线性Granger因果关系,结果表明在10%的显著性水平下,各市场量价之间仅存在双向的线性Granger引导关系。这说明过去的日内交易量对现在的日内收益的预测有显著的作用,反之亦然。同时更重要的应用是可以建立日内收益和交易量的线性模型来进行拟合和预测。然后,根据信息经济学理论,采用高频数据建立SVAR模型对我国A、B股市场之间的量价信息传递特征进行了全面的研究。基本结论如下:
1)在单个的A股或B股市场内部,收益的自相关是短期的,而交易量的自相关则是长期的。两个市场均只有收益到交易量的Granger引导关系而没有反向的因果关系。
2)A股或B股市场的量价之间有交易量到收益的当期因果关系,该市场交易量对当期收益的有明显的信息传递,证明了成交量是股价趋势的先行指标。同Darrat等(2003)一样支持序贯信息到达假设。
3)A、B股市场之间的信息流是双向传导的,相对于2001年2月之前A、B股市场完全分割的历史,随着B股市场对国内投资者开放和A股QFII、QDII政策的实施,两个市场的分割得到很大改善,信息在两个市场之间可以顺畅的传递。但是,两个市场间的信息传递占优的方向仍然是从A股市场到B股市场,信息主要是在A股市场发现,B股市场陷入功能缺失的困境,这是一个亟待解决的问题。
本书的不足之处是由于数据稀缺,没有足够的高频数据将B股对国内投资者开放事件对A、B股市场量价信息传递变化进行对比。而本书要研究沪港股市的信息传递的初衷更是由于数据不可获得无法实现,极大影响了本章的完整性。
5. 2 我国股票市场的波动溢出检验
5.2.1 引言
全球资本市场一体化背景下,金融市场的放宽和交易技术的提高使得信息在不同市场之间的传导速度大大加快、传导渠道日渐增多,金融市场之间的相互依赖、相互影响也与日俱增,金融时间序列间的相关性如相关程度、协同运动、波动的传导和溢出等问题的研究也因此成为一个热点。香港回归祖国10多年了,中国加入WTO也有多年了,这些年来,沪市与港市之间是否存在波动溢出效应?波动溢出的方向如何?从较长的时段看,两市之间的关联程度发生怎样的变化,并呈现出哪些新的特征?这些问题的研究对于投资者判断股市走势、预测和分散投资风险和政策制定者防范金融危机等都有非常重要的意义。
由于1987年的股市大崩盘事件,Eun和Shim(1989)和Becker等(1990)开始研究国际股票市场之间相互依存的特性,这是研究波动溢出的第一批文献,但当时前者采用的方法是VAR模型,后者则是基于单方程的线性回归。由于资本市场波动往往表现出典型的非正态分布特征,采用这些传统回归方法很容易得出“有偏”和“非一致”的估计结果,而GARCH类模型因为可以刻画时间序列呈现的波动聚类现象,成为波动建模的有力工具。第二代研究如Hamao等(1990),Lin et al.(1994)正是采用GARCH框架来考虑金融序列内在的条件异方差性。这些研究仔细考虑了不同国家股票交易(trading segments)时间的顺序、恰当定义了日度收益和日内收益。但是这些研究一般局限于一个市场对另一市场的外生冲击,单向考察波动溢出不一定准确。为避免变量“内外生性”判断的武断性,第三代研究将GARCH类模型从单变量扩展为多变量,提出了多元广义自回归条件异方差模型(MGARCH),从而提供了多元波动分析的一般框架。由于该模型既能捕捉金融时间序列尖峰厚尾、波动丛集的特性,又能反映不同序列之间相关的时变特征,MGARCH模型此后获得了迅速的发展,常见的有BEKK、CCC以及Engle(2002)的DCC。
从统计学意义上讲,检验波动溢出就是检验条件方差序列之间是否存在Granger因果关系。事实上,目前几乎所有研究波动溢出的实证文献采用的方法更像是Granger(1969)型(type)检验,即在MGARCH模型的框架下以一个变量的残差平方对自身和其他变量的残差平方滞后项做回归。Cheung和Ng(1996)提出采用经其条件方差估计量标准化后的两残差平方之间的样本交叉相关函数(cross correlation function,CCF)来检验波动溢出,统计量服从高阶卡方分布。这种检验相对比较简单且可以为MGARCH建模提供有价值的信息,但本质上仍然属于Granger(1969)型检验。而Hong(2001)对此方法进行了改进,引入核权函数对低阶时滞赋予较大的权重,刻画近期的波动比远期的波动对当前的波动影响会更大的特点,同时允许使用的样本交叉相关系数个数M随着样本规模T的增加而增加,即可以使用所有的滞后信息,从而确保该法在较长的滞后阶数下仍保持较强的检验功效。
中国股市正处于发展阶段,近年来经常出现大幅波动,但是对股市间收益、波动关系比较系统性的研究却较少。上证指数和深证指数的相关性极强,不同板块间也明显存在着不同程度的相关性,这在众多文献如刘金全和崔畅(2002)、赵留彦和王一鸣(2003)已有证明。谷耀和陆丽娜(2006)采用了复杂的DCC-(BV)EGARCH-VAR模型检验了沪、深、港股市信息溢出效应与动态相关性,该模型选择香港为影响内地股市的“世界因素”并作为外生变量引入还值得商议,同时该文仍然只研究了沪深股市的相关性.本书拟采用Hong(2001)的方法检验沪、港股市之间信息的传播方向.本书的研究方法逻辑清楚,得到的结论也更为可靠.
5.2.2 波动溢出检验(Hongtest)
1)统计量的构建.Hong(2001)首先通过GARCH建模得到各市场的标准残差平方,然后利用基于加权CCF的方差间Granger因果检验来检验波动溢出.单一市场的模型形式采用实证研究中比较流行的GARCH(1,1)模型,模型参数采用准极大似然法(QMLE)估计.
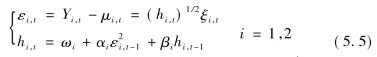
其中Yi,t表示i市场t时刻的收益率,ui,t=E(Yi,tIi,t-1),为i市场t时刻的条件均值,Ii,t-1为i市场t-1时刻的信息集.hi,t为i市场t时刻的条件方差,ξi,t为满足E(ξi,tI1,t-1)=0,Var (ξi,tI1,t-1)=1的独立白噪声过程.
现对H0∶![]() 进行检验(其中It-1 =(I1,t-1,I2,t-1)).如果H0成立,则说明Y2,t-1不是Y1,t的方差Granger原因.Hong通过检验标准残差平方μt=
进行检验(其中It-1 =(I1,t-1,I2,t-1)).如果H0成立,则说明Y2,t-1不是Y1,t的方差Granger原因.Hong通过检验标准残差平方μt=![]() 与νt=
与νt=![]() 间滞后j阶的交叉相关函数ρuv(j)是否为0来检验H0.令T为样本容量,按如下(5.6)式可得μt与νt间的样本交叉相关函数.
间滞后j阶的交叉相关函数ρuv(j)是否为0来检验H0.令T为样本容量,按如下(5.6)式可得μt与νt间的样本交叉相关函数.
![]()
其中样本交叉协方差函数![]() 1),样本方差分别为
1),样本方差分别为![]()
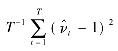 .
.
Hong(2001)证明了k(z)= sin(πz)/πz为最优的核权函数,并以此为核权函数构造Q1统计量如式(5.7):
![]()
其中C1T(k)=![]() (1-j/T)k2(j/M),D1T(k)=
(1-j/T)k2(j/M),D1T(k)=![]() (1-j/T)(1-(j+ 1)/T)k4(j/M)。
(1-j/T)(1-(j+ 1)/T)k4(j/M)。
在H0成立的条件下,Q1在大样本条件下服从渐近的N(0,1)分布,依此统计量可检验2市场是否对1市场产生了单向波动溢出。值得一提的是,通过检验标准残差ξ1,t和ξ2,t的j阶交叉相关函数ρ(j)是否为0,Hong(2001)可直接延伸用于检验均值Granger因果关系。
2)数据基本分析。本书采用上证指数和恒生指数的每日收盘价{Pt}为样本。考虑到1997年香港股市因为亚洲金融危机出现异常的波动,选取样本时间段为1999年1月04日至2006年9 月1日,排除仅有单一市场交易的天数,共1841组有效数据。所有数据来源于Wind数据库。收益率序列{Yt}为: Yt= ln Ptln Pt-1,分别以Y1和Y2表示,即上海股市和香港股市分别用1市场和2市场表示。表5-4给出了样本区间内Y1和Y2的基本描述统计量。
表5-4 Y1和Y2的基本描述统计量

可见,Y1的标准差相比较大,反映出其波动性较大的特征。Y1与Y2的分布呈现出不同的特征,Y1为右偏,Y2为左偏。Y1与 Y2的峰度均大于3,说明两序列相对正态分布而言呈现明显的尖峰特征,JB统计量也表明Y1、Y2的分布均呈现显著的非正态性。两序列滞后5阶自相关检验的Q统计量(用Q(5)表示)以及相应的p值在5%的检验水平上Y1不显著,表明Y1、Y2没有明显的自相关特征,这说明模型中均值方程的设定充分。收益平方序列的滞后5阶自相关系数的Q统计量(用Q2(5)表示)均在1%的检验水平上显著,表明收益序列存在明显的ARCH效应,因此应用GARCH类模型对Y1与Y2进行描述。
3)实证结果及分析。在检验方差Granger因果关系时必须过滤掉均值Granger因果关系的影响,否则均值Granger因果关系的存在将会夸大甚至产生虚假的方差Granger因果关系。因此研究两市场间的波动溢出时应首先剔除能够用本市场的收益滞后项和它市场的收益滞后项预测到的条件均值部分,而仅取不能预期的收益成分来分析。为此首先对条件均值方程引入AR模型来消除这种自相关。就本研究而言,数据基本分析已显示Y1、Y2各自没有明显的自相关,同时若设定为滞后阶p>0时AR(p)-GARCH模型,AR项的系数估计值均不显著,A IC值并没有减少,这也说明p= 0。
第二步考虑两市场间收益的跨期互相关关系,如果这种相关性不显著,则用单变量AR模型来刻画条件均值就是充分的。如前所述,通过检验标准残差ξ1,t和ξ2,t的j阶交叉相关函数ρ(j)是否为0,Hong(2001)可直接用于检验均值Granger因果关系。检验结果见表5-5,表明港市不是沪市的收益Granger原因,沪市也不是港市的收益Granger原因,因此在估计1(2)市场的条件均值时,不必加入2(1)市场收益的滞后项,上一步的模型设定充分。
采用准最大似然法对两市场的GARCH模型估计结果如表5-6所示,两个模型条件方差方程所有变量均在5%的水平下显著。标准残差的Q(5)和Q2(5)统计量的p值均大于10%,说明经GARCH建模后序列不再存在自相关现象和波动聚类现象。
表5-5 两市场间的均值Granger因果关系检验
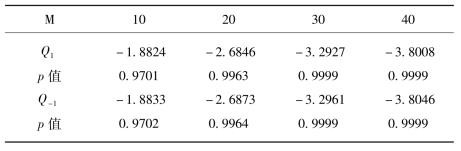
表5-6 沪、港股市的GARCH(1,1)模型估计

沪市的α+β≌0.97,这意味着波动冲击衰减很慢,波动聚类现象严重。港市的参数α+β≌1,表示该市场近似为IGARCH过程。图5-2是序列Y1与Y2的条件方差时变特征图,显示出两市场波动水平差别很大,沪市收益的波动曲线大部分时间都在港市波动曲线的上方,说明上海市场的波动水平要高于香港市场。具体来说,1999年的“5.19行情”明显对应沪市波动的最大值点。2001年的国有股减持到减持方案暂停,沪市的波动连续出现了几轮巨大的峰值,一直持续到了2002年。之后沪市持续低迷,波动水平也一直维持在一个较低的幅度上。而港市在2001年之前因受金融危机和国际金融市场动荡的影响波动略为偏大一些,之后就一直非常平稳。可见,沪市多次剧烈波动,投机气氛十分浓重;而港市则表现出其成熟股市的特征。

图5-2 Y1与Y2的条件方差时变特征图
通过估计GARCH模型得到两个市场标准残差平方的估计量![]() 和
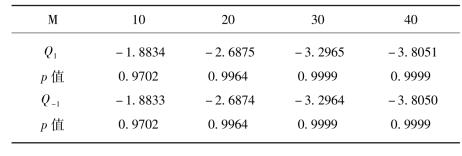
和![]() ,并用(5.7)式构造统计量Q1来检验港市是否对沪市产生了单向波动溢出,同理也可构造Q-1统计量来检验沪市是否对对港市产生了单向波动溢出。计算过程通过Matlab6.5编程实现。遵循Hong(2001),其中M= 10,20,30,40。由表5-7可以看出,Q1、Q-1统计量p值均大于0.95,表明港市未对沪市产生波动溢出,沪市也未对港市产生波动溢出。此检验结果对两市场的条件方差建模提供了非常有益的信息,1(2)市场的条件方差方程不必加入2(1)的滞后收益平方项作为解释变量。波动溢出效应的不存在性表明:沪市面临的冲击源主要是沪市证券特有或市场特有的要素的变化,而港市证券或市场的变化并不明显对沪市产生冲击。反之亦然。象收益信息一样,波动信息也没有明显的、流畅地在两市场之间传递。
,并用(5.7)式构造统计量Q1来检验港市是否对沪市产生了单向波动溢出,同理也可构造Q-1统计量来检验沪市是否对对港市产生了单向波动溢出。计算过程通过Matlab6.5编程实现。遵循Hong(2001),其中M= 10,20,30,40。由表5-7可以看出,Q1、Q-1统计量p值均大于0.95,表明港市未对沪市产生波动溢出,沪市也未对港市产生波动溢出。此检验结果对两市场的条件方差建模提供了非常有益的信息,1(2)市场的条件方差方程不必加入2(1)的滞后收益平方项作为解释变量。波动溢出效应的不存在性表明:沪市面临的冲击源主要是沪市证券特有或市场特有的要素的变化,而港市证券或市场的变化并不明显对沪市产生冲击。反之亦然。象收益信息一样,波动信息也没有明显的、流畅地在两市场之间传递。
表5-7 两市场条件方差间的因果关系检验
5.2.3 结论
本书采用基于加权CCF的方差Granger因果检验方法,分析了上证指数、恒生指数收益序列的波动溢出效应,并以此信息为依据建立BEKK模型对两序列的时变波动相关性进行了实证,结果表明:①相对香港股市收益稳定、波动小的时变特征而言,上海股市具有收益不稳定、风险高等新兴市场特点;②两市场之间的收益信息传递并不明显,同时波动溢出也不显著,任一市场的冲击对另一市场的波动产生的传导性影响不明显,上海股市与香港等成熟股市的即时联动性较小。
5. 3 基于时变Copula的我国股票市场相依性研究
5.3.1 引言
金融市场风险分析一直是国内外关注的课题,对资产收益的相关性研究在风险分析中尤为重要。传统的相关性假设资产收益服从多元高斯分布,此时相关系数即可度量金融资产的相关程度,在这种假设下相关性较弱的两种或多种资产收益同时取尾部极值的可能性非常小。而事实上1997年的亚洲金融危机,1998年的俄罗斯和巴西的金融危机都说明,金融市场风险可能同时发生在不同国家,甚至发生在相关程度很低的一些国家。原来线性相关系数可直接用来度量相关性的条件是相当苛刻的:首先,相关系数要求变量间的关系是线性且其方差为有限,否则就没有定义,但是金融市场中出现的不少数据往往是厚尾分布,其方差有时并不存在,此时就不能用线性相关系数来反映相关性;另外,线性相关系数无法捕捉变量间非线性的相关关系,而在椭圆分布之外的相关结构往往是非线性的,此时再用线性相关系数作为相关性的测度极有可能导致错误的结论。因此更多的时候我们必须选用其它相关性指标才能得到变量间真实的相关关系。
在不能确定线性相关系数能否正确度量相关关系时,有一种更灵活稳健、更为可靠的分析变量间相关结构的相关性分析工具——Copula技术。由于金融风险中各类风险之间的关系常常是非线性的,而Copula函数能较好地捕获非线性相依关系。同时由于相关性会随着市场的波动性而发生变化,具有条件时变特性,尤其是在市场发生重大冲击时,更要采用时变相关模式来描述。中国股市现在处在发展阶段,近年来经常出现大幅波动,因此本书重点讨论上证指数和香港恒生指数的时变和尾部相关性关系。
5.3.2 Copula-GARCH模型的构建
基于Copula方法度量金融市场的相关性有三个关键环节。①要选择合适的边缘分布及相关结构。②采用两阶段极大似然估计法对模型中的参数进行估计。③对模型的拟合优度进行检验。也就是说第一步是确定随机变量的边缘分布,然后选用适当的Copula函数,以便能很好地描述出边缘分布的相依结构。
Copula-GARCH模型是将GARCH模型和Copula函数有机地结合在一起用来分析多个金融时间序列的分布特性和相关关系。首先采用GARCH模型描述不同金融时间序列的条件边缘分布,根据条件边缘分布函数对各序列进行概率积分变换,得到的新序列可以通过一个Copula函数来连接,此Copula函数可完全刻画各序列间的相关结构。Copula-GARCH模型不仅可体现出金融时间序列的条件异方差特性,又可从概率的角度反映序列间非线性的相关关系,非常适合于分析金融市场的相关性。所以本书首先结合t-GARCH模型和二元正态Copula函数来构建Copula-GARCH模型:
1)确定边缘分布模型。Copula方法的特点是,如果边缘函数正确则结果非常可靠,而如果边缘函数错误则之后的分析没有意义,所以边缘分布的拟合非常重要。由于t分布可以很好地描述金融时间序列的条件分布多呈现的时变、偏斜、高峰、厚尾等特性,而GARCH模型又能很好地描述金融时间序列的波动特性,因此t-GARCH模型可以更好地描述金融时间序列的波动聚类和高峰、厚尾现象。一般采用t-GARCH(1,1)模型就可以较好地描述各收益序列的波动,该模型的表达式为:

其中,收益率rt是εt的函数,容易证明rt与εt同分布,因此式(5.8)可用来刻画收益序列的边缘分布。
如果要重点对两变量的尾部即极值相关性进行建模,通常选择分布的尾部两端用广义Parato分布(GPD)、中间部分用经验分布来描述变量的边缘分布。GPD的含义是指超过一定阈值的随机变量近似地服从广义Parato分布。其边缘分布定义中有两个重要的指标分别代表上尾阈值和下尾阈值。阈值的选择对于边缘分布的参数估计非常关键。阈值过大,超过阈值的量就会太少,用这些较少数据估计出的模型偏差可能过大;而阈值过小,数据特征不明显,不能准确地刻画变量的尾部特征。一般采用Stuart(2001)介绍的方法选取阈值。实际应用中还可根据研究对象的不同采用GARCH类或SV类模型来描述相应收益序列的边缘分布。事实上,边缘分布的建模已经相当成熟。
2)确定Copula函数。由于相关性会随着市场的波动性而发生变化,具有条件时变特性,尤其是在市场发生重大危机和异常波动时,更要采用可以描述尾部相关的时变相关模式来描述,所以下面介绍几种动态Copula。
(1)时变相关的二元normal Copula模型。常用来描述通常情况下两个变量相关结构的二元正态Copula函数分布函数如前公式(4.3)。其静态Copula形式中相关参数ρ为常数,此时ρ就是Φ-1(u)和Φ-1(v)的线性相关系数,而在动态Copula形式中ρ就是时变的。为了研究变量间相关关系随时间变化的这种特性,Patton经研究提出此时的ρ可以由一个类似于ARMA(1,10)的过程来描述:
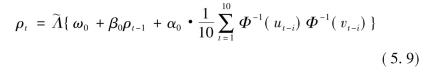
其中![]() ,引入该函数是为了确保ρt始终处于(-1,1)区间内。由于回归变量ρt-1可以捕捉到相关性参数的持续性,而滞后10阶的观测值的转换变量Φ-1(ut-i))与Φ-1(vt-i)乘积之和的均值可以捕捉到相关性的变化,因此式(5.9)可以用于捕捉序列间时变的条件相关关系。
,引入该函数是为了确保ρt始终处于(-1,1)区间内。由于回归变量ρt-1可以捕捉到相关性参数的持续性,而滞后10阶的观测值的转换变量Φ-1(ut-i))与Φ-1(vt-i)乘积之和的均值可以捕捉到相关性的变化,因此式(5.9)可以用于捕捉序列间时变的条件相关关系。
(2)时变相关的二元Joe-Clayton Copula模型。二元正态Copula函数的分布具有对称性和尾部渐进独立性,因此无法捕捉到变量间的非对称相关和尾部相关,而Joe-Clayton Copula函数则可以很好地描述变量间的非对称相关和尾部相关特性。因此在实际应用中,Joe-Clayton Copula函数常是一种更好的选择。
Joe-Clayton Copula函数的参数与尾部相关系数有一一对应的关系,其非条件形式为:
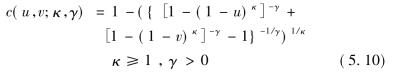
对应的尾部相关系数分别为:τU= 2-2-1/κ,τL= 2-1/γ。公式特点是上尾相关系数完全由参数κ确定,而下尾相关系数则完全由参数γ确定。由于确定参数时变过程的主要困难在于定义演变方程的外生变量,通常只有知道参数的某些含义才能知道影响参数变化的因素。而利用上述这种一一对应的关系,Patton定义了Joe-Clayton Copula函数中参数的动态演化过程。
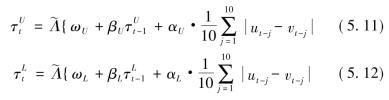
其中函数Λ()为logistic转换函数,定义为:![]() ,其运用同样是为了确保上尾和下尾相关系数始终处于(0,1)区间内。演化方程(5.11)、(5.12)和(5.9)一样,也是类似于一个ARMA(1,10)模型,方程的右边都包含一个自回归项和一个外生变量。这里选用滞后10期的ut与vt的差的绝对值的均值作为外生变量,作为度量数据与完全正相关之间距离的指标。
,其运用同样是为了确保上尾和下尾相关系数始终处于(0,1)区间内。演化方程(5.11)、(5.12)和(5.9)一样,也是类似于一个ARMA(1,10)模型,方程的右边都包含一个自回归项和一个外生变量。这里选用滞后10期的ut与vt的差的绝对值的均值作为外生变量,作为度量数据与完全正相关之间距离的指标。
由于上尾和下尾相关系数与Joe-Clayton Copula函数的两个条件参数有一一对应的关系,样本的尾部相关参数的演化过程同时确定了Copula参数的演化过程。可见用Copula函数来分析金融风险分析中资产间的尾部相关性非常方便。
5.3.3沪港两股票市场相关结构的实证分析
为了考察上海、香港两股票市场间的相关变化规律,本节采用上证指数和恒生指数的每日收盘价{Pt}为样本。考虑到1996年12月16日后开始实行涨跌停板限价交易,而1997年香港股市因为亚洲金融危机出现异常的波动,选取样本时间段为1999年1月4日至2006年9月1日,排除仅有单一市场交易的天数,共1841组有效数据。所有数据来源于Wind数据库。收益率序列{Yt} 为:Yt= ln Pt-ln Pt-1,分别以Y1和Y2表示。图5-3是上证和恒生指数对数收益序列图。

图5-3 上证和恒生指数对数收益序列图
1)边缘分布模型的估计结果与分析。分析发现,用式(5.8)所示的t-GARCH(1,1)模型就可以较好的描述上海股市和香港股市指数收益序列的边缘分布,采用极大似然估计法对各收益率序列的边缘分布进行估计,得到表5-8所示结果。
指定的边缘分布模型能否很好的拟合变量的实际分布,对Copula函数能否正确地描述变量间的相关结构至关重要,因此必须建立评价边缘分布拟合优度的方法。Dieboid等(1999)建立了基于序列概率积分变换的密度分布模型的评价方法,适用于Copula模型的评价。表5-8中的K-S统计量及其概率值就是根据估计得到的边缘分布,对原序列做概率积分变换,再运用K-S检验方法,检验变换后的序列是否服从[0,1]均匀分布所得到。
表5-8 沪、港股市的t-GARCH(1,1)模型估计
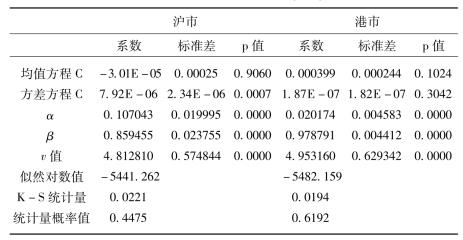
表5-8中的K-S统计量及其概率值表明,对各序列均没有充分的理由拒绝零假设:“变换后的序列服从[0,1]均匀分布”。另外,对变换后的各序列做自相关检验发现,变换后的各序列均不存在自相关,因此可认为变换后的序列均是独立的。K-S统计量和自相关检验表明,根据t-GARCH(1,1)模型估计得到的边缘分布对原序列做概率积分变换后得到的序列均服从i. i.d(0,1)均匀分布,说明用t-GARCH(1,1)模型来描述各收益序列的边缘分布是充分的。
对于t分布,自由度v的值与t分布尾部的形状是紧密相关的,自由度越小则分布的尾部越厚。从表5-8中自由度v的估计值可以看出,与香港恒生指数收益序列的分布相比,上证指数收益的分布有更厚的尾部,这说明上证指数收益出现极端值的概率较大,这与上海股票市场常常大涨大跌的实际表现是相符的。
2)Copula函数的估计结果与分析。为了对比考察沪港两指数收益序列之间的静态和动态相关关系,分别用常相关的二元正态Copula函数和时变相关的二元正态Copula函数来描述两序列的相关结构。
图5-4是采用正态Copula函数拟合得到的上海股市和香港股市的收益序列之间相关参数ρ的常数图和时变图。由常相关参数ρ的值0.1065可以看出,上海股市和香港股市的收益率序列之间呈现正相关关系,但相关的程度较弱。从投资组合的角度看,选择资产相关性小的资产进行组合,可以降低投资风险,上海股市和香港股市收益率序列之间静态的相关关系分析表明,通过组合上海股市和香港股市的方式来可以较好的降低投资风险。
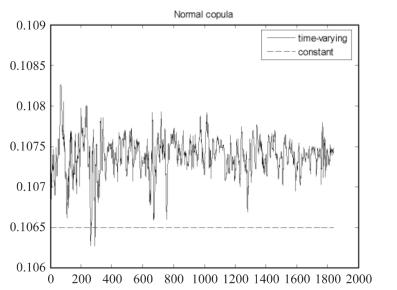
图5-4 正态Copula拟合的相关参数图
图5-4中动态Copula的时变相关系数ρt介于0.10625和0.10825之间。可见相关系数变动范围并不大,在总体值大小方面来说,动态Copula的时变相关系数的值也都比较小。这和韦艳华研究上海股市各板块之间相关系数都在0.95以上的值相比较起来,显得非常小。这再一次说明上海股市和香港股市的相关程度较小,两个市场联动性较弱。

图5-5 J-C Copula拟合的尾部相关参数图
图5-5是采用Joe-Clayton Copula函数拟合得到的上海股市和香港股市的收益序列之间尾部相关参数的常数图和时变图。通过图5-5的上下两个图的对比明显可见,上海股市和香港股市在下尾的相关性比起上尾来说要强的多,两市场的非对称性相关规律比较明显。在上尾,两个市场的相关性几乎为零,也就是说几乎没有相关性,这主要和上海股市追涨的心理非常强烈导致股市在上涨时连续暴涨的因素有关。而在下尾,也就是在两个市场都处于低迷的状态的时候,两个市场的相互影响显得要明显的多。这说明在市场低迷的时候,两个市场的投资者相对来说更加在意另一个市场的涨跌情况,跟风的趋势相对要强。
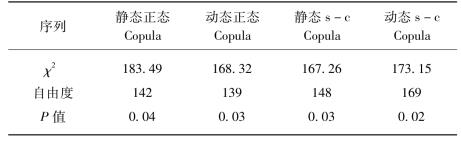
本书总共采用4种Copula:正态Copula和Joe-Clayton Copula以及各自的动态形式。各种Copula模型估计时的logl值等见表5-9。由表5-9可以发现,不管是根据极大似然值logl还是按照AIC值或SC值进行拟合优度的排序,结果都一样。一个普遍的规律是动态Copula模型的比静态的拟合效果要好,考虑尾部相关的Copula模型比没有考虑尾部相关的拟合效果要好。
表5-9 各种Copu la模型的拟合优度排序

总体来说,不管是常相关还是时变相关的Copula,考虑尾部相关的Joe-Clayton Copula比正态Copula的拟合效果都要好的多,这说明上海股市和香港股市的相关性确实具有明显的非对称性。这种非对称相关性的原因从投资者角度可以认为:人们对利空消息的敏感程度要远远大于利好消息的敏感程度。当一个市场出现暴跌情形时,人们会感到很紧张,就会立即采取行动;相反,当一个市场出现上涨趋势时,人们关心的程度并不像下跌情形时那样立刻跟进。
3)各种Copula函数的拟合优度比较。最后对构造的模型按照第1.2节拟合优度检验的基本原理,构造一个20×20个单元格的表格G。可以算得每种Copula下每个单元格内实际数据观测频数以及由模型预测的数据频数,这里把观测频数小于5的单元格合并,所以每种Copula下自由度不一定相同。由此可以算得每种Copula下的χ2统计量的观测值。从检验结果表5-10可以得到以下结论。首先,在显著性水平α= 0.05下各种Copula都通过了拟合优度检验,说明用这几种Copula函数可以较好地描述各个时期变量间的相关结构。其次,通过各检验p值的进一步比较则发现,拟合的效果排序和由AIC原则排序得到的结果相同,即都是Joe-Clayton Copula比正态Copula好,动态比静态的要好。这也再一次说明沪港两个市场的相关性具有明显的不对称性,投资者在熊市时对于可能的亏损比起在牛市时的盈利更为关心和紧张。同时也提醒政策的制定者在熊市时密切关注两个市场的动态以便进行相应的决策防止风险的蔓延。
表5-10 Copula模型的拟合优度检验
5.3.4结论
金融资产相关结构的研究是金融市场风险分析的重要内容之一。过去对风险分析的研究主要集中在金融资产收益的分布上,而忽略了市场风险与个股风险的不同作用。近几年对资产间相关结构的研究引起了人们的广泛重视。本书运用Copula技术讨论了金融市场的相关模式问题,构建了4种Copula-GARCH模型,并对沪港股市相关性进行了实证研究。结论如下:Joe-Clayton Copula比正态Copula好,动态模型比静态的要好。这表明,沪港股市确实存在非对称的相关变化规律,且下尾相关性明显高于上尾,熊市效应显著。也说明传统意义下的高斯相关结构确实不能较全面地反映金融资产间的相关关系,尤其是在刻画尾部相关性上还不够。
5. 4 QFII对A、B股市场分割的影响的实证研究
5.4.1 引言
QFII(Qualified foreign institutional investors)即合格的境外机构投资者,是指允许经批准的机构投资者,在一定规定和限制下汇入一定额度的外汇资金,并转换为当地货币,通过严格监管的专门账户投资当地证券市场,其资本利得、股息等经批准可转化为外汇汇出的一种市场开放模式。作为一种有创意的引进外资,开放资本证券市场的过渡性安排,QFII制度是那些货币还未完全自由兑换,资本项目尚未开放的新兴市场国家或地区实现有序、稳妥开放证券市场的特殊通道。
2002年11月7日,中国证监会和中国人民银行联合颁布了《合格境外机构投资者境内证券投资管理暂行办法》。随后人民银行、外汇管理局、深沪交易所和证券登记结算公司相继颁布了一系列相关规章,标志着中国合格的境外机构投资者制度的正式确立。2003年5月23日,瑞士银行有限公司被批准为境内首家QFII。随后摩根士丹利、花旗环球、高盛和汇丰等境外机构投资者相继获得进入中国股市的资格,对中国境内股、可转债和基金等证券市场产品进行投资。
QFII制度自开始实施以来,审批一直很严格,其间由于担心资金投机人民币升值,曾经几度暂停。转折发生在2005年4季度,政策面开始放宽,不仅额度从40亿美元提升到100亿美元,审批也明显加快。2006年《合格境外机构投资者境内证券投资管理办法》颁布使得QFII的申请门槛大幅降低、资金锁定期大幅缩短、额度上调,为更多机构进入中国市场创造了机会。QFII对股市场的投资热情相当高,特别是自股权分置改革以下简称“股改”以来,明显增加了对A股的投资。截至2006年末获得资格的境外机构共52家,其中44家机构获得投资额度,已批准QFII的投资额度累计达90.45亿美元,44家QFII持有A股的总市值已经达到971亿元,占沪深两市该年末流通总市值的比例达到3.88%,一跃成为A股市场仅次于基金的第二大机构投资者。
另一方面,中国A、B股市场的市场分割由来已久。其主要的制度障碍在于在2001年2月19日B股对境内投资者开放以前,国内投资者只能交易A股而国际投资者仅能交易B股,这样A、B股两个市场便被完全分割。这种分割使得实际中B股的交易远没有A股活跃,其相对于A股也存在着明显的折价。从股价变动和成交量来看,B股更是长期低迷。但由于对A、B股投资者和交易币种的硬性限制,使得此套利空间无法成为现实的获利。2001 年2月19日,中国证监会发布通知,允许境内居民以合法持有的外汇开立B股账户,交易B股股票。根据吴文锋等(2002)的研究,市场对此事件反应异常剧烈,B股投资者规模迅速扩大,B股价格迅速飙升,折价程度大幅下降。从活跃B股市场的角度看,这确实实现了管理层的初衷。但是,虽然B股对境内居民开放缩小了两个市场之间的壁垒,但是A、B股之间仍然差价巨大,B股的价格仅为A股的60%。对境内居民开放为什么没有完全消除市场分割?此次引入QFII是否进一步削弱了两个市场之间的分割而达到一体化呢?对这些问题的深入研究将有助于了解A、B股两个市场的分割状况和原因,有利于解决A、B股市场的分割,实现两个市场的一体化,而这一直也是发展和规范我国证券市场的一个重要课题。
由于目前符合条件入境交易的均为大机构投资者,通常宣扬注重基本面分析、注重长期投资的投资理念,因此在当前的中国股市,QFII被市场视为富有理性且投资经验丰富的投资者,认为其起到了稳定市场的作用。但上述认识基本建立在一种直观感觉之上,对于QFII的交易是否真如我们想象般理性、是否起到了稳定股市的作用、是否进一步削弱了两个市场之间的分割,却缺乏实证研究的支持。事实上,QFII对在我国证券市场交易行为的研究几乎是空白,其原因主要在于并不向公众披露其交易信息,外界只能从上市公司定期报告中公布的十大股东的变化来推算得到少量的交易数据。例如孙立和林丽(2006),耿志民(2006)等,均仅限于一些基本的描述统计分析,难以对的交易行为进行更深人的研究。本节采用事件分析法,通过对2004年1月至2006年3月间交易数据的研究,对QFII制度推行之初和股改期间QFII大规模实施这两个事件是否明显导致A、B股的价差和收益差的减少进行了全面的考察和分析。
5.4.2 数据和方法
1)样本数据的选取。本研究的数据样本为在上海证券交易所和深圳证券交易所同时发行A股和B股的股票,去掉在样本时期(指事件前后两期)非正常交易(指PT类股票)的股票后,上海证券交易所有38只股票,深圳证券交易所有37只。QFII自2003 年7月开始交易深市A股,但2003年获批额度的QFII家数较少,故本节从2004年开始考察其交易行为,样本数据包括2004年1月至2006年3月间合格境外投资者总体交易数据。
为了观察QFII在推行过程中产生影响的变化,我们将时间段划分为QFII制度推行之初和股改期间QFII大规模实施两个阶段,也就是股改前(2004年1月至2005年4月)和股改期间(2005 年5月至2006年3月)。另外,为了与“B股向境内居民开放”事件的影响进行比较,本节针对相同的研究对象,同时研究了“向境内居民开放B股”对A、B股市场分割的影响。
2)研究假设和方法。鉴于本节在前一节所述两种市场分割或一体化检验方法的局限性,本节的研究方法是直接从市场一体化或分割的基本定义出发,即直接考察制度变革前后同一家公司A、B股价格和收益率差异的变化趋势,来考察两大事件对A、B股市场一体化的作用程度。
根据陈小悦(2005)的观点,A、B股票收益率差异套利活动的载体是资金,尽管人民币尚未实现完全可兑换,但人民币与外币之间兑换的渠道是存在的,所以,在B股对境内开放的背景下,资金套利行为将使A、B股的收益率差异逐渐降低,直至完全消失(扣除人民币与外币兑换过程中的交易成本因素)。另外,A、B股股价差异套利活动的载体是股票,A、B股在两个市场进行交易、不能跨市场买卖,所以现阶段仍无法通过套利活动消除A、B股股价差异。B股向境内投资者开放也有助于缩小A、B股股价差异,其机理不在于资金的套利行为,而在于此项措施增加了投资B股的潜在的和现实的资金供应,由于供求关系和投资者的心理预期决定B股价格会有大幅上升,A、B股股价差异下降。因此,B股向境内投资者开放会同时缩小A、B股股价差异和股收益率差异,其不同之处在于作用机理不同。
本节的假设和陈小悦(2005)的有所同有所不同。一方面,各个事件对A、B股价差和收益差(绝对值)的下降应该有显著的作用。这一点本节同样认同。但另一方面,因为两个市场之间除了硬分割因素之外还有许多软因素,这些因素加上还没消除的硬因素,使得两个市场的价差收益差将长期存在,不可能完全消失。
本节设定两个指标Pab、Rab来衡量A、B股的价差和收益差,并通过该指标在某一事件前后期的变化来度量该事件对A、B股的价差和收益差的影响及其程度。指标定义如下:Pab= Pa-Pb,Rab=Ra-Rb,即实证检验中都是以B市场作为基准。其中Pa、Pb分别代表A、B市场的价格,Ra、Rb分别代表A、B市场的收益。
5.4.3 实证结果
1)QFII制度实施事件的影响。
(1)QFII制度推出事件的实证结果。本节首先对QFII制度推出这个事件对A、B股的价差和收益差的影响做相应检验,结果见表5-11。
表5-11 QFII制度推出事件的实证结果

从表5-11可看出,QFII制度的推出事件对A、B股的价差和收益差有明显的影响。在QFII制度推出之前A、B股的价差率平均取值为0.4901。而在QFII制度推出之后,A、B股的价差率平均取值为0.5027。通过对事前、后价差序列进行检验,发现事前后价差的变化非常显著,同期A、B股的收益差变化同样非常显著。但奇怪的是,在此事件前后,A、B股价差和收益差没有像预期的那样减少,反而是增加的.这说明QFII制度的推行对A、B股的价差的下降和收益差的绝对值的下降并没有显著的作用,原因可能是由于QFII制度的推行速度太慢,实施的规模在初期一直较小,对市场资金面的影响微不足道。至于不降反升的深层原因,下文将做进一步探究。
(2)QFII制度大规模实施事件的实证结果。为了观察QFII制度较为深入的实施事件对A、B股的价差和收益差的影响与QFII制度推出事件所产生影响的不同,本节对股改时QFII大力实施对A、B股的价差和收益差的影响也做相应检验,结果见表5-12。
表5-12 QFII制度大规模实施事件的实证结果
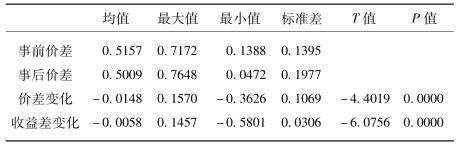
从表5-12可看出,QFII制度大力实施事件对A、B股的价差和收益差有明显的影响。在刚刚通过相关制度到2005年股改之前,A、B股的价差率平均取值为0.5157,而在股改事件后期,A、B股的价差率平均取值为0.5009。通过对事前后价差序列进行检验,发现事前后价差的降低非常显著,同期A、B股的收益差降低同样非常显著。这说明随着制度设计的不断完善以及QFII资金额度的不断扩大,对内地证券市场的影响逐渐加深,对A、B股的价差和收益差(是指的绝对值)的下降有显著的作用。这也和国际经验是一致的。
2)B股向境内居民开放事件的影响。为了探究较长时期A、B股的价差和收益差变化行为,本节还对向境内居民开放B股这个事件对A、B股的价差和收益差的影响做了相应的检验,结果见表5-13。
从表5-13可看出,在此事件前期,即B股对境内居民开放之前,A、B股的价差率平均取值为0.7996,而在事件后期,A、B股的价差率平均取值为0.4861,通过对事前后价差序列进行检验,发现事前后价差的变化非常显著,同期A、B股的收益差变化同样非常显著。这说明B股对境内居民开放对A、B股的价差和收益差绝对值的下降起了非常显著的作用,这也与陈小悦(2005)的计算的数据比较接近,结论也是一致的。
表5-13 B股向境内居民开放的实证结果

综合本节前后所有的检验可以发现:在本节所研究的整个时期,即由从2000年到2006年,A、B股的价差和收益差经历了一个先下降再上升然后又下降的过程,按照理论的预测,A、B股的价差和收益差应该一直是下降的,而中间之所以有一段时间是上升的,很可能是由于B股对境内居民开放对A、B股的价差和收益差绝对值下降的影响的市场反应明显过度。也就是说,投资者对B股对境内居民开放对A、B股的价差和收益差绝对值下降寄予的期望过高,在操作时投机性很强,使得A、B股的价差和收益差绝对值在短期内迅速下降,但是当投资者的投资激情又迅速退却之后,A、B股的价差和收益差绝对值在此后的较长一段时间内又有一段比较缓慢的回弹即上升。
5.4.4 结论
本节采用事件分析法,通过对2004年1月至2006年3月间交易数据的研究,对QFII制度推行之初和股改期间QFII大规模实施这两个事件是否明显导致A、B股的价差和收益差的减少进行了全面的考察和分析。结果显示,以2005年5月股权分置改革开始将研究样本分为两个时间段,股改前QFII制度的推行对A、B股的价差的下降和收益差的绝对值的下降并没有显著的作用,随着制度设计的不断完善以及QFII资金额度的不断扩大,QFII对内地证券市场的影响逐渐加深,对A、B股的价差和收益差(是指的绝对值)的下降有显著的作用,的确进一步削弱了两个市场之间的分割。B股对境内居民开放对A、B股的价差和收益差绝对值的下降起了非常显著的作用,但是市场投资者的对该事件的反应明显过度。
5. 5 本章小结
本章采用了以Copula为核心的多种相关性研究方法、依次从信息传导、波动溢出和相关模式的角度对我国股票市场的相关性进行了实证研究。
首先,本章按照从一般到特殊的计量建模顺序建立了合适的模型对我国股票市场的信息传导进行了实证研究。采用高频的5分钟数据检验了上海和深圳各股市价格和交易量之间的线性和非线性Granger因果关系,结果表明各市场量价之间仅存在双向的线性引导关系,并不存在非线性Granger因果关系。基于这个结论,本章根据信息经济学理论,建立SVAR模型对我国A、B股市场之间的量价信息传递特征进行了全面的研究。主要结论为:A、B市场之间的信息流是双向传递的,但是信息传递的方向主要是从A股市场到B股市场,信息主要是在A股市场发现。
其次,本章从波动溢出的角度探讨了我国沪、港股市联动性程度。即采用基于加权CCF的方差Granger因果检验方法,分析了上证指数、恒生指数收益序列的波动溢出效应,结果显示两市场之间的波动溢出并不显著,任一市场的冲击对另一市场的波动产生的传导性影响不明显。
最后,本章运用Copula技术讨论了金融市场的相关模式问题,构建了4种Copula-GARCH模型对沪港股市相关性进行了实证研究。结论表明,两股市的联系和联动性较小,上海股市的波动具有相对的独立性。沪港股市确实存在非对称的相关变化规律,且下尾相关性明显高于上尾,熊市效应显著。
“B股市场向境内居民开放”、“QFII制度的推行”以及后续的“QDII制度的推行”都是影响整个B股市场环境的几个重大事件。本章第4节从另一个侧面研究了我国A、B股市场从分割走向一体化的进程。第4节采用事件分析法对QFII制度推行之初和股改期间QFII大规模实施是否明显导致A、B股的价差和收益差的减少进行了全面的考察和分析。结果显示,股改前QFII制度的推行对A、B股的价差的下降和收益差的绝对值的下降并没有显著的作用,随着制度设计的不断完善以及QFII资金额度的不断扩大,对内地证券市场的影响逐渐加深,对A、B股的价差和收益差的绝对值的下降有显著的作用,“QFII制度的推行”尤其是大规模实施确实进一步削弱了两个市场之间的分割。
总的来说,在过去的20年间,虽然中国B股市场为中国的经济发展、金融深化以及国际化历程做出过重要的贡献,然而,在中国经济获得了快速发展、资本市场不断深化过程中,中国B股市场遭遇诸多问题并逐渐被边缘化的事实,已经引起高度的重视。早在2000年5月,当时的中国证监会首席顾问梁定邦就多次在不同场合明确表示:国内的A、B股市场,随着外资在A股市场业务的不断扩大,将会在2到3年内自然走向合并。然而,时间过去了这么久,举措也推出了不少,A、B股市场的合并还在漫漫征途当中,可见,这将是一个长期的难题。
本章的不足之处是由于数据的稀缺性,没有获得恒生指数同期的高频数据以实现研究沪、港股票市场信息传递的初衷,使得本章的体系完整性受损。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















