4.1公司外汇风险暴露模型及其向市场层次的扩展
外汇风险暴露估计模型是以资产定价模型为依托的,因此,本文在介绍外汇风险暴露估计模型之前对资产定价理论进行简要的回顾。资产定价理论是研究如何对资产进行估价的理论,是旨在研究和决定具有不确定未来收益的索偿权的价值或价格的经济学理论,与公司财务、金融市场与机构共同构成现代金融学的三大核心领域。对资产定价问题的研究起源于18世纪,Bernouli(1738)提出的边际效用递减概念为后来的经济学家发展风险决策理论奠定了基础。1952年,马柯维茨创造性地把收益率的标准差作为风险的量度,将精确的数理模型引入金融分析中,提出了资产组合理论,创立了不确定条件下的金融决策理论,标志着现代金融学的诞生。自此,现代资产组合理论、资本资产定价理论、行为资产定价理论等理论成果层出不穷,这些理论成果可以划分为传统资产定价理论阶段和行为资产定价理论阶段两个阶段。无论是传统资产定价理论还是行为资产定价理论都对金融理论和实践产生了巨大的影响。由于本文是对外汇风险暴露估计模型所依托的资产定价模型进行探讨,因此,对行为资产定价模型就不再一一列举。
4.1.1 基本的资产定价模型
4.1.1.1 现金流贴现模型

现金流贴现模型在传统金融学中是一种重要的定价方法。在加入不确定性分析后成为现代金融资产定价理论的重要组成部分。现金流贴现模型集中体现了资金的时间价值特性。任何资产的价值都是由其未来现金流的现值所确定的,以复利计算为基础的现金流贴现模型可用公式(4-1)表示:其中,P为资产现在的价格,CF为将来各时点的现金流,ρ为折现率,是该模型的关键,用无风险利率加上风险补偿来表示。无风险利率是指货币资金在不承担任何风险的情况下可以取得的收益率,通常用短期国债利率来表示;风险补偿取决于金融资产风险的大小,理性的投资者都是风险厌恶的,资产风险越大,被要求的风险补偿也就越高。现金流贴现模型十分简单方便,但是该模型并没有对风险补偿的程度进行定量分析,对该缺陷的研究,萌生了现代资产组合理论。
4.1.1.2 现代资产组合理论(Modern Portfolio Theory,MPT)
为了减少投资者总量风险,Markowiz于1952年提出现代资产组合理论。其风险分散原理是:多种证券组合的总收益等于个别证券收益的加权平均,而组合的总风险可以比个别证券的风险小。一般而言,高的收益率往往伴随着高的风险,任何一个投资者或者在一定风险承受范围内追求尽可能高的收益率,或者在保证一定收益率条件下追求风险的最小化。理性的投资者通过选择有效的投资组合,实现期望效用最大化。
Markowiz的模型以资产回报率的均值和方差作为选择的对象,而不去考虑个体的效用函数。一般来说,资产回报率的均值和方差并不能完全包含个体作选择时所需要的信息。但是,在假设效用函数为二次的或者资产回报率服从正态分布的前提下,个体的期望效用函数能够仅仅表示为资产回报率均值和方差的函数,从而,投资者可以只把资产回报率的均值和方差作为选择的目标。该模型的本质是使投资组合在给定收益率水平上实现风险最小化,并具体说明在该收益率水平上投资组合中各种风险资产的类型及权重。求解的结果是一条双曲线,其中双曲线的上半支是有效组合边界,投资者在有效组合边界上根据其风险—收益偏好选择投资组合,结果必然是投资者的效用函数与有效组合边界的切点。
由于“均值-方差模型”的灵活性以及经验上的可检验性,应用较为广泛。“均值-方差模型”自提出以后得到了长足的发展。后期,研究者在Markowitz模型框架中引入不对称信息、流动性限制、交易成本等因素来研究投资者的最优投资组合问题,并且取得了一定的成效。但是该模型在确定有效组合边界的过程中,需要确定任意两项资产的协方差,即投资组合理论考虑到了影响一项资产价格的任何一个方面,但正是这种完备性使得它要处理的数据量异常庞大,使投资组合理论在实际中不具有现实操作性。
4.1.1.3 资本资产定价模型(Capital Asset Pricing Model,CAPM)
Sharpe(1964),Lintner(1965),Mossin(1965)分别独立地提出资本资产定价理论(CAPM理论)。该模型将无风险资产引入到现代资产组合理论体系中,运用均值与方差的概念并利用求极值的简单思想,推演出一个对应于各种特定风险下投资资产组合的可行机会集合曲线(Pportfolio Opportunity Set,即资本市场供给曲线),和一个由投资者根据相应的风险资产与无风险资产构成的风险资产组合(即资本市场需求曲线),把证券的超额回报率与市场证券组合的回报率联系起来,并用β系数描述单个证券与整个市场的关系,以及β系数与证券的收益率和风险的关系。
![]()
公式(4-2)表明,在市场均衡时E(ri)等于第i项资产的市场资本化率,即第i项资产的预期收益率,β系数是一个重要概念,衡量单项风险资产与市场组合之间风险补偿变动的相关性,它是应用CAMP的关键。
资本资产定价模型是一个简洁优美的模型,将选择风险资产的复杂过程简化到了“傻瓜式”的程度,实用性很强。但是从理论角度讲,资本资产定价模型过于笼统,影响一种资产价格变动的因素很多,资本资产定价模型试图用市场这个单一因素来解释所有问题有些牵强。
此外,CAPM模型的前提假设相当苛刻,该模型要求投资者是理性的,他们遵循均值-方差效用函数,且其边际效用大于零;所有投资者面临相同的无风险利率,并可以自由地按无风险利率借入或贷出资本;证券市场是有效的,即信息是免费的并且瞬间可得;证券交易不征税,也没有交易成本,证券市场是无摩擦的;每种证券的收益率分布均服从正态分布。CAPM模型由于严格的假设条件而受到很大的限制,同时,市场资产组合的指向是模糊的,使得对其的准确的实证检验无法进行。
此外,Lucas(1978)、Merton(1990)等人指出,CAPM是一个简单的静态的投资组合优化模型,无法描述投资者的跨期投资行为,他们在静态资本资产定价模型的基础上提出了跨期的动态资本资产定价模型——ICAPM。ICAPM分为离散时间模型和连续时间模型两种。离散时间模型以Lucas的资产定价模型为代表,假设投资者在离散的时间点上进行投资和消费决策,并且各期的产出量与消费量相等。该模型以投资者的效用最大化为目标函数,导出资产价格与边际效用之间的关系,再结合产出与消费的均衡关系,得到用边际效用函数表示的资产定价方程。Cox等(1985)、Merto(1990)等人提出的连续时间模型中,假设投资者连续地进行投资和消费,推导过程的本质是在既有财富的约束下使投资者终身消费的效用达到最大,通过求解最优的消费—投资方案得到资产定价的基本方程,再结合代表投资者的间接效用函数和财富过程,解出资产的价格。
4.1.1.4 套利定价理论(Arbitrage Pricing Theory,APT)
无套利分析方法是用价格已知、并且未来的预期收益现金流与该资产完全一致的资产或资产组合对待定价的资产进行复制,构造一个不能产生无风险收益的组合,进而为该项资产定价。现代金融理论的研究取得的一系列成果都是基于这种“无套利”的分析技术形成的。Ross(1976)提出套利定价理论(APT)是建立在多因素进行个体套利行为之上的一种均衡模型。通过消除套利机会,套利者使市场更具有效率。套利定价理论认为:当多个宏观经济因素共同影响一种风险资产的预期收益时,该资产的预期收益可以表示为:
![]()
在对多因素APT模型的因素及其数目选择的研究中,比较有代表性的是,Fama和French(1993)提出的三因素模型,该模型明确指出影响股票收益的因素是市场因素(market factor)、规模因素(size factor)和净值市价比因素(book to market value ratio)。该模型强调只要在股票定价模型中考虑这三个因素,以往研究所指出的定价盲点就会消失,他们证明三因素模型能够解释80%左右的美国股票收益变化,在其他市场(包括中国在内的新兴股票市场)也发现了类似的证据。Fama和French也指出了模型的缺陷:从理论角度来看,该模型未考虑投资者预期因素。此外,三因素模型的明显缺陷是不能解释收益动能现象,在三因素模型的基础上加上动能因素,即四因素资产定价模型便能增强资产定价模型对收益变动的解释能力。
APT与CAPM的重要区别是,CAPM是均衡条件下的资产定价模型,而APT的理论基础是“不存在无风险套利机会”。因此,APT成立的前提是完全竞争和有效资本市场,其要求的条件要宽松得多,这使得它有了更为广阔的应用空间。与CAPM相比,APT在更加广泛的意义上建立了证券收益与宏观经济中其他因素的联系,将资本资产定价从单因素模式发展成为多因素模式,从模型的真实、准确度来讲,套利定价模型所得出的预期收益的数据的实用性比资本资产定价模型大大增加,更加接近市场实际,为证券走势分析提供便利。可以说,APT是复杂化、多元化了的CAPM,在内涵和实用性上更具广泛意义,既是对CAPM的肯定,更是一种补充和修正。
当然,APT模型也存在重要缺陷,一是该理论没能确定影响资产价格的因素到底有多少,分别是哪些;二是与CAPM一样,对其进行严格意义的实证检验也很困难(Shanken,1985)。
20世纪80年代中期以后的20多年里,金融学家们从不同角度对资产定价模型进行检验,新的研究从根本上否定了资产定价理论的结论,主要表现在:一是单个资产、资产组合、基金和投资策略的平均收益与其β系数不相称;二是收益并不是随机游走的,具有一定程度的可预测性;第三,股票收益表现出很强的中期动能和长期回归倾向。传统的资本资产定价模型缺乏实证证据的支持,运用心理学、社会学、行为学来研究金融活动中人们的决策行为的行为金融学便成为学界关注的焦点。
4.1.2 公司外汇风险暴露的理论模型及其扩展
4.1.2.1 现金流模型
早期大多数对外汇风险暴露的理论研究是以公司现金流为基础的。1973年布雷顿森林体系崩溃以来,汇率波动幅度日益提高。相应地,公司的当前和未来的现金流的波动幅度也随之增大。现金流的波动提高了公司利用资本市场融资的必要性,也增加了与此相关的融资成本,从而降低投资水平和公司价值。(Shapiro和Titman,1985;Froot等,1993;Minton和Schrand,1999)。Choi(1986)将外汇风险暴露定义为汇率变动对未来公司现金流量折现值的影响。Richard C.Marston(2001)在资产定价的现金流量分析法的基础上提出了外汇风险暴露的现金流模型。即
![]()
其中,V为资产现在的价格,CF为将来各时点的现金流,等于公司税后利润加上净投资,ρ为折现率,是由无风险利率表示,通常用短期国债利率来表示。如果净投资为零,且未来每年的现金流相等,税率为τ,税前利润为π,则有:
![]()
如果St为名义汇率变动率,则外汇风险暴露可以表示为V对S求导,即:
![]()
假设税率τ和折现率ρ均为常数,则外汇风险暴露取决于税前利润。
假设公司产量为X,其中X0的产量以P0的价格在国内销售,X1的产量以P1(外币价格)的价格在国外销售,由于在国内外出售的产品是无差异的,因此,其成本是总产量的函数。假定企业生产成本有两种货币形式,其中本币成本表示为CD,外币成本表示为CF,则总成本为:CD(X0+X1)+SCF(X0+X1),则反需求函数为P0=D0(X0),P1=D1(X1)
公司以本币表示的利润如下:
![]()
利润最大化的一阶条件是:
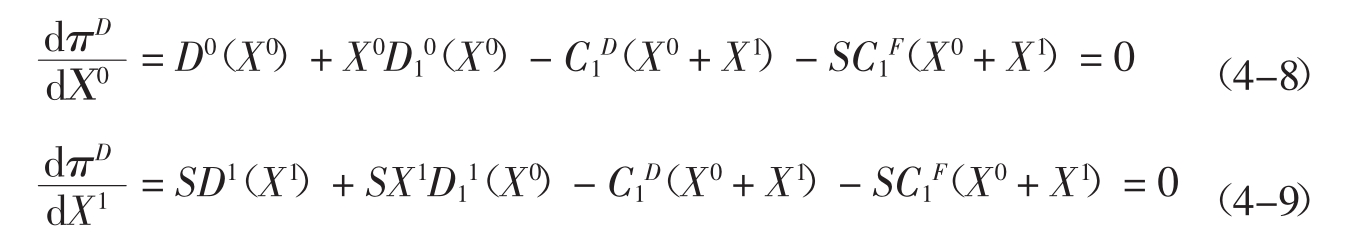
式中,每个方程对产量的一阶导数都用下标1来表示。模型中外汇风险暴露用利润对汇率的导数表示,即
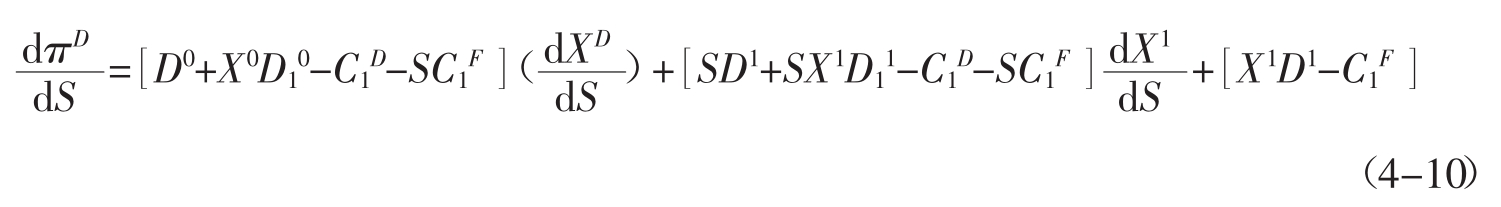
如果公司处于利润最大化的均衡状态,则前两个方括号项都为零,那么,上式简化为:
![]()
外汇风险暴露即利润对汇率的导数就等于外币净收入,即外币收入与外币成本之间的差额,如果本币升值(dS<0),那么本币表示的利润将以公司净收入的一定比例下降。
4.1.2.2 AdlerDumas资本市场模型
由于现金流模型需要大量的公司自身和竞争者的内部数据,获得这些数据的困难使人们无法对公司外汇风险暴露进行比较,Adler和Dumas(1984)根据公司未来现金流的折现值就是公司的现值的假设,将公司市场价值作为公司现金流的代理变量,提出外汇风险暴露可以用公司价值对汇率波动的系数来衡量,而这个系数可以从公司的股票收益率对汇率变量进行的简单回归中得到。这种方法极大地方便了外汇风险暴露的测算,使外汇风险暴露的大规模研究和比较分析成为可能。此后的大部分关于外汇风险暴露的文献,皆以公司的股价作为公司现金流的代理变量。其模型形式如下:
![]()
式中,Ri,t表示公司i在t阶段的回报率,St是t阶段的汇率,β1,i是i公司的外汇风险暴露系数,描述i公司股票的回报率对汇率变化的敏感性,β0,1是常数项,εi,t白噪声项。
4.1.2.3 Jorion扩展的市场模型
Jorion(1990)认为外汇风险暴露可以分解为宏观风险暴露和剩余风险暴露,宏观风险暴露是指汇率变动及其引起其他宏观经济变量的变化带来的股票收益率的变化,表现为市场收益率对汇率变动的敏感程度,剩余风险暴露是指超出市场对汇率变化反应的那部分风险暴露。Adler和Dumas(1986)的估计方法中i公司的外汇风险暴露只是简单地通过公司股票回报变化对汇率变动的回归系数来衡量,得出的是公司的全部外汇风险暴露,该模型未将与汇率和股票回报同时发生变动的其他宏观经济变量纳入其中,将会导致外汇风险暴露系数的高估。所以,应在Adler-Dumas模型基础上加入市场投资组合报酬率作为控制变量,来衡量i公司的剩余暴露。其模型形式如下:
![]()
式中,Ri,t表示公司i在t阶段的总回报率,Rmt是t阶段整个股票市场的回报率,β1,i是公司i对市场风险的敏感性,St是t阶段的汇率变动,β2,i是公司i独立于市场的外汇风险暴露系数,衡量的是i公司股票回报率对汇率变动的剩余敏感性,β0,i是常数项,εi,t白噪声项。[1]
在模型中加入市场投资组合报酬率变量有两个好处。首先,加入市场组合报酬率变量可以控制与公司价值相关的宏观经济因素的影响,使得风险暴露的估计在不同的时间跨度和时间段更加稳定。其次,公司股票回报率与市场回报率相关性较强,把市场回报率包含在公式中减少了随机误差项的方差,提高了风险暴露估计的准确性。此外,在使用Jorion的公司剩余外汇风险暴露的概念时,某个企业的风险暴露弹性系数为零并不意味着该企业价值独立于汇率波动,而是该企业的外汇风险暴露程度与市场组合的风险暴露程度相同。
4.1.2.4 对Jorion模型的扩展
对Jorion模型的实证检验可谓汗牛充栋。但实证检验的结果表明外汇风险暴露并没有理论上那么大[Jorion(1990)、Miller和Reuer(1998)、Katrina Bradley,Peter Moles(2001)],为此理论界开始探讨模型是否遗漏了重要变量,并从不同角度对模型进行了扩展。
1.外汇衍生品的引入
Levi(1994),Booth(1996)认为外汇风险暴露水平的显著性低可能是因为进行了有效套期保值活动。Crabb(2002)将风险暴露系数的估计与外汇衍生品的使用联系起来,他将外国资产的水平、外国收入的水平和外汇衍生品使用的强度引入到Jorion扩张的市场模型中。
![]()
其中,C1it代表国外利润水平,C2it代表国外资产,C3it代表外汇衍生品的使用。与先前关于套期保值活动影响研究相一致,Crabb的研究认为外部套期活动倾向于降低公司的风险暴露。然而,Nguyen和Faff(2003)、Muller和Verschoor(2004)的研究结论表明外汇衍生品的使用对公司外汇风险暴露在统计上只有微弱的影响。
2.宏观经济变量的引入
Horst Entorf,Gosta Jamin(2002)认为宏观因素对股票回报和汇率都有影响。而AdlerDumas模型和Jorion模型都是在资本资产定价模型(CAPM)的基础上检验外汇风险暴露情况,为了控制其他潜在的宏观经济风险因素如通货膨胀和利率波动等,该研究用套利定价模型(APT)替代了CAPM,并进一步检验外汇风险暴露与潜在的协变量之间的关系[2]。模型形式如下:
![]()
其中,r代表N个股票价格的收益向量,μ是N种证券的预期收益向量,fK是包括汇率波动的现实中的K个因素,包括德国经济景气程度、通胀率、期限结构、剩余市场因素[3]以及美元汇率。B是N乘K的矩阵,表示N种证券对K种因素的敏感程度,ε是N种证券的误差项构成的向量。预期收益μ可以被分解为:μ=λ0+BλK,其中λ0是无风险利率,λK是K种因素的风险溢价向量,将上述两式合并,可得
![]()
![]()
研究结果表明,进口商和出口商的外汇风险暴露程度不同,且具有时变性。与先前的研究认为不存在外汇风险暴露的观点相比,他们证实了Dominguez和Tesar(2001)的观点,即在德国,与外国经济联系越紧密的企业,外汇风险暴露水平越高,此外,他们还发现外汇风险暴露的水平取决于美元汇率的水平。
3.将Jorion模型推广到汇率变动对股票市场影响的研究
Timothy K Chue,David Cook(2008)将Jorion模型用于发展中国家股票市场外汇风险暴露的研究,并在研究中引入了国际股票市场的超额回报率。其模型形式如下:其中,Rj,t表示j国股票市场的本币收益率,Rw,t表示以美元衡量的国际股票市场的收益率[4]。Sx,j表示j国的贸易权重汇率,模型中引入国际股票市场的收益率主要是为了避免引入其他的国际变量与误差项之间的内生性问题。该研究发现外汇风险暴露是时变的,在1999~2002年间本币贬值对新兴股票市场有负向影响,在2002~2006年间该趋势却消失了。
本书对外汇风险暴露模型的发展及其扩展进行了系统的梳理,从现金流模型到Jorion的资本市场模型再到对Jorion模型的扩展,反映了理论界对外汇风险暴露的理解和认识在不断深入。尽管迄今为止尚没有一个模型能够将汇率冲击对公司价值乃至股票市场的复杂影响因素囊括其中,但是大量的证据表明汇率波动在一定程度上影响市场走势和股东财富,从这种意义上来说,汇率变动对股票市场的影响在理论和实践意义上都应当引起重视。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。













