汇率变动对股票市场影响估计方法的发展

4.2汇率变动对股票市场影响估计方法的发展

4.2.1　汇率设定问题

4.2.1.1　双边汇率、贸易权重汇率还是相关货币汇率

Jorion模型对汇率风险因素的设定并没有明确规定，实证研究中大多使用双边汇率或者贸易权重汇率，一般双边汇率选择该国的主要贸易伙伴国货币汇率（Williamson，2001；Priestley和准degaard，2004），贸易权重汇率则在分析该国汇率综合水平的变动对股票价格的影响时使用。Choi等（1998）认为使用不同汇率所得出的研究结论并不一致，因此，汇率风险因素的设定对汇率对股票市场影响系数的估计有显著作用。这就引发了估计该系数时的汇率选择问题。由于双边汇率无法全面反映该国汇率变动的情况，而贸易权重汇率不仅忽视了汇率之间的低的负相关问题（Miller和Reuer，1998），而且抹杀了双边汇率之间的差异从而低估了汇率的影响程度，Williamson（2001）认为如果一国或公司主要是面临几种货币风险，那么使用双边汇率或贸易权重汇率都是缺乏解释能力的。

为了减轻双边汇率和贸易权重汇率对汇率对股票市场影响的估计造成的偏误，西方学者采取多种方法对汇率风险因素的设定进行了探索。Khoo（1994）在对澳大利亚采矿业的研究中，通过考虑每个子样本公司贸易伙伴的重要性来选择汇率。Miller和Reuer（1998）通过使用主成分分析法来选择汇率风险因素进而将最相关的货币汇率引入到模型中来，并对美国制造业公司的外汇风险暴露情况进行分析，该方法能够揭示更高比例的公司存在外汇风险暴露，Ihrig（2001）也为不同的公司建立了独特的汇率指数，该指数由该公司有分支机构的国家货币组成，并发现使用这些汇率指数比以往的研究中其他汇率指数估计得到的影响系数要显著得多。

Fraser和Pantzalis（2004）则认为在汇率选择过程中应当将更多的货币包含在汇率指数中，并证明使用该汇率指数时，更多的公司有显著的外汇风险暴露。这为公司暴露于其未经营未涉及的货币的汇率风险提供了证据。

4.2.1.2　名义汇率和实际汇率的选择

经济理论表明在模型估计过程中为反映汇率变动对股票市场的真实影响，应当使用实际变量，但多数研究使用的是名义变量，这主要是出于两方面的原因：一是通货膨胀数据的周期性限制了投资者的使用。由于金融市场没有即时的通货膨胀数据，投资者很可能使用名义汇率来分析其对股票价格的影响（Bodnar和Gentry，1993），因此，名义汇率可能更能反映外汇风险暴露的真实情况。二是一般情况下月度的通货膨胀率与汇率变化相比幅度较小，投资者容易忽略通货膨胀的作用，这意味着名义变动实际上所起到的作用要大于实际变动。因此，在研究中使用名义汇率还是实际汇率的差别不大（Bodnar和Gentry，1993;Chamberlain等1997）。

4.2.1.3　滞后变量的引入

由于认知水平的限制，投资者不能在短期内立即对汇率波动的影响进行评价，因此，汇率对股票市场的影响存在时滞。Bartov和Bodnar（1994）认为在公司过去绩效已知的条件下，投资者学会了随时间变化更有效地评价汇率变化对公司价值的全部影响，投资者的这种行为会导致汇率与公司价值之间存在滞后关系。他们建议将股票回报对常数项和当前以及滞后的汇率变动进行回归，其结果表明汇率变动对公司价值的影响是有时滞的，该时滞一直持续到过去的经营绩效、公司的资产负债信息被发布为止。He和Ng的发现表明样本中的日本公司对汇率有显著的滞后反应的不超过4％，因此，引入汇率变动的滞后项对提高模型的解释能力没有显著影响。Chin-Wen Hsin等（2007）在Fama和French的三因素模型的基础上，引入了汇率变动的滞后项，该研究表明滞后项的引入显著提高了公司外汇风险暴露的显著性。

4.2.1.4　汇率的自相关问题

实证研究表明，多数货币的汇率变动存在正的自相关（Amihud和Mendelson，1989）。为此，Amihud（1994）建议使用两步法来消除汇率的自相关问题。第一步是汇率变化对其滞后变量进行回归；第二步是估计Jorion模型，将θ_t用第一次估计的残差dθ_t代替。但是Amihud的方法并没有使得估计结果的显著性获得明显提高，Gao（2000）建议将汇率对宏观经济变量的滞后项进行回归，来消除汇率的自相关问题，其模型形式如下：式中，IR_t代表利率，M_t代表货币供给，Y_t代表行业的产量，TB_t表示净出口，π_t表示t阶段的通货膨胀率。Gao（2000）检验了消除自相关的汇率对80个跨国公司的冲击，通过模型得出的系数比最初的汇率变动序列更为显著。

4.2.2　市场组合回报的选择及其与汇率风险存在的多重共线性问题

4.2.2.1　市场组合回报的选择

虽然市场风险因素的引入减轻了遗漏变量问题，市场风险因素的设定对风险暴露系数的符号、大小和显著性有直接影响。大多数学者通常选择的市场组合是价值权重组合，这种方法使得大公司在市场组合中占有更多的权重，因此，大公司的影响力更大。为了减少这种偏误，Bodnar和Wong（2000）使用等权重市场组合来代替价值权重市场组合，来控制宏观经济因素在风险暴露估计中的影响。等权重市场组合中大公司和小公司占有相同的权重，这样更能从总体上反映汇率对整体市场价值的影响。Bodnar和Wong（2003）在估计公司的外汇风险暴露时选择公司规模为基础的投资组合作为反映市场条件的控制变量，由于公司规模与外汇风险暴露之间的关系是不规则的且大的公司在指数中的权重较大，使得风险暴露系数存在正的偏误，因此，应当给那些以出口为导向的存在现金流暴露的公司赋予更大的权重。Mahesh D Pritamani等（2004）运用Jorion模型对1997年12月标准普尔500中的主要从事进口、出口和国内业务的公司的外汇风险暴露进行检验。发现运用不同的投资组合所得的结论也不尽一致，因此，估计系数的精确性取决于作为的控制变量的市场投资组合的选择。

4.2.2.2　市场风险和汇率风险的多重共线性

1.通过正交化处理来消除多重共线性

由于市场组合回报和汇率变动之间存在较高的相关性，Jorion模型可能存在多重共线性问题。为了避免多重共线性导致的任何偏误，Choi和Prasad（1995）选择了经过正交化处理的汇率风险因素。该方法是Elton和Gruber（1991）建立的，通过汇率对市场风险因素进行偏回归，然后使用Jorion的资本市场模型来估计外汇风险暴露，将其中的θ_t用市场风险不能解释的汇率风险部分来代替。Kiymaz（2003）则通过经过正交化处理的市场回报来解决多重共线性问题，即通过使用市场回报对汇率波动的进行回归得到的残差来代替原来的市场组合回报，在这种情况下，dR_mt代表不能被汇率变动解释的市场回报部分，新系数λ_i衡量的是i公司的全部外汇风险暴露。此外，还可以通过将市场回报和汇率波动与宏观经济变量之间进行正交化处理来消除多重共线性。如Doukas等（1999）将其他的风险因素如公司规模和金融萧条引入Jorion模型。

式中，V_jt前定的宏观经济变量，包括行业产量增长、未预期的通货膨胀率、期限结构、货币供给、美国和日本的利差以及贸易余额，dR_kt代表从四个风险因素对前定的宏观经济变量和这些因素各自的滞后变量回归中获得的四个未预期的风险因素变化即汇率变化、市场回报率和账面市场权益比的变化、小公司与大公司的回报率的差异。由于宏观经济变量和滞后变量是时变的，外汇风险暴露也是时变的。模型的应用表明外汇风险暴露在日本股票市场是显著的。

2.通过引入市场组合回报的代理变量来消除多重共线性

也有学者试图通过研究汇率变动和市场回报之间的关系来解决Jorion模型面临的多重共线性问题。Miller和Reuer（1998）认为由于相同的因素如利率变动会引起汇率和市场回报都发生变动，因此应将这些因素作为解释变量引入模型。Chow和Chen（1998）为了避免市场组合收益对估计结果的干扰，将对市场组合回报有解释能力的商业条件变量引入模型中：

式中，D_it和T_it是指t阶段主要的股息红利收益和期限溢价。S_t表示实际汇率的变化率。尽管他们的发现表明一些日本公司存在显著的外汇风险暴露，但其结果与没有包括商业条件变量时没有差异。

Gao（2000）用六个宏观经济变量M_kt来代替市场风险，这些宏观经济变量是公司价值的基本决定因素，在衡量外汇风险暴露时为防止高估的发生必须将其包括在内：

这里宏观经济变量M_kt代表关于失业率、生产者价格指数、货币供给、能源价格指数以及总工资指数和产业工资指数的联系变化。dS_t表示汇率变化对其主要决定因素回归进行的正交化过程中得到的未预期的汇率变化。通过将这些影响股票回报和汇率变动的基本因素考虑在内，等式旨在降低内生性问题。实证研究表明外汇风险暴露系数在多数情况下是统计显著的，但是如果用市场风险代替这六个宏观经济变量则风险暴露系数不再显著。

4.2.3　汇率变动对股票市场影响的时变性

4.2.3.1　时变的影响系数的估计

时变性是该研究领域最有争议的一个问题之一。Jorion（1990）估计模型实际上隐含了公司外汇风险暴露系数是常数的假设。但是这一假定是不符合现实的，因为整个经济环境、公司的竞争地位、经营结构以及其保值策略是不断变化的。Levi（1994）认识到应当对汇率对股票市场的影响系数以特殊的计量技术予以明确的模型化，否则该影响的不稳定会使得这种影响不显著。这种时变性可以通过如下几种方法进行估计：

一是通过将时间序列分为几个子区间来分别检验该系数是否是常数，（Jorion，1990;Glaum等，2000;Doukas等，2003）。Williamson（2001）关于汽车行业的实证分析中，每一个子样本区间的影响都与该部门面临的竞争环境相关。总之，所有的这些研究都支持影响是时变的这一假设。二是通过控制市场变量来估计。Bodnar和Wong（2003）在估计汇率对股票市场的影响时，如果模型控制了市场变量，则所得到的系数是稳定的，如果没有控制市场因素则得到的系数是时变的。

4.2.3.2　时变性的起因的研究

汇率变动对股票市场影响的时变性激发了人们对其起因的研究兴趣，Levi（1994）认为时变性是公司的套期保值策略不稳定造成的。Allayannis（1995）证明了在时变的影响系数估计与实际经营和进出口的变化相关的假设条件下，汇率变动对美国制造业的影响程度是与在这些行业中的进出口份额相关的。Gao（2000）认为本币贬值（升值）对国外销售的正向影响（负向影响）和对在国外设立的公司的市场份额有负向影响（正向影响），为了区分汇率波动带来的这两种效应，他将汇率的影响设为公司外销占全部销售额的比例F_it和国外公司的产量占公司总产量的份额X_it的函数：

式中，待估系数φ_1i和φ_2i分别衡量的是汇率变动对国外销售和对国外生产的影响，φ_3i是对剩余效应的估计。F_it和χ_it都是时变的，汇率影响系数β_i也允许是时变的。Gao的研究结果表明该系数有预期的符号（φ_1i为正和φ_2i为负）并在统计上都是显著的。模型的实证应用对公司销售和生产决策以及如何通过这些决策降低汇率风险提供了有益的帮助。

4.2.3.3　观测频率的选择

汇率影响系数的时变性引发了观测频率的选择问题。尽管理论认为在市场有效的情况下，实证结果应当独立于观测频率，但实证研究的结论表明由于市场通常是无效的、汇率变动和股票市场以及公司价值之间的关系复杂，估计的系数是随观测频率和时间间隔而变化的。一些学者对最常用的观测频率即月度观测进行研究，发现该频率捕捉公司的外汇风险暴露是不显著的。但多数学者认为时间间隔的拉长有助于提高估计系数的显著性，Dominguez和Tesar，（2001）、Muller和Verschoor（2004）认为时间间隔越长股票回报对汇率变动越敏感。这是因为人们瞬时的认识上的偏差会导致股票价格和汇率暂时偏离它们的基础价值数据，随着时间的推移和认识偏差的消失而股票价格会逐步回复到其真实价值上来。当时间跨度足够大时，暂时的错误定价的影响相互抵消，从而发现汇率与股票收益率的基本关系。

4.2.4　汇率变动对股票市场影响的不对称和非线性设定

在AdlerDumas模型提出后，理论界大多沿用了对汇率和股票收益之间线性关系的设定。这意味着无论汇率变化的大小或方向如何，公司都没有对汇率变化做出不同的反应。然而，越来越多的理论模型提出公司对汇率变化会做出不同的反应，并对非线性的外汇风险暴露估计模型进行了探索。

4.2.4.1　汇率影响的不对称性

1.公司在本币升值或贬值时会采取不同的行为

Krugman（1987）认为如果外国公司扩张其销量的成本很高的话，在美元升值时，进口价格将不会下降。相比之下，美元贬值就不会有这种效应，因此，汇率的影响是有差异的。Froot和Klemperer（1989）研究了在公司产品的未来需求取决于当前和未来的市场份额的条件下，汇率变动对进口价格的传递。认为在本币升值或贬值预期是暂时的还是永久性两种情况下，公司的行为是不对称的。Knetter（1994）认为如果公司的生产规模受限或者有出口配额，在贬值或升值期间的加价效应将会有差异。此外，公司为了保护市场份额，很可能在升值和贬值期间采取不同的策略。

为衡量本币升值和贬值时的不对称的影响，Koutmos和Martin（2003a）对Jorion模型进行扩展，其模型形式如下：

如果S_t<0，则D_t=1，否则为零，系数β_D，s如果显著则代表汇率变动存在不对称的影响，该模型假定影响系数为常数，且假定汇率是外生的，由于这一假定并不能成立，从而引发同期相关问题。

Gregory Koutmos，Anna D.Martin（2007）在此基础上将时变性引入模型：

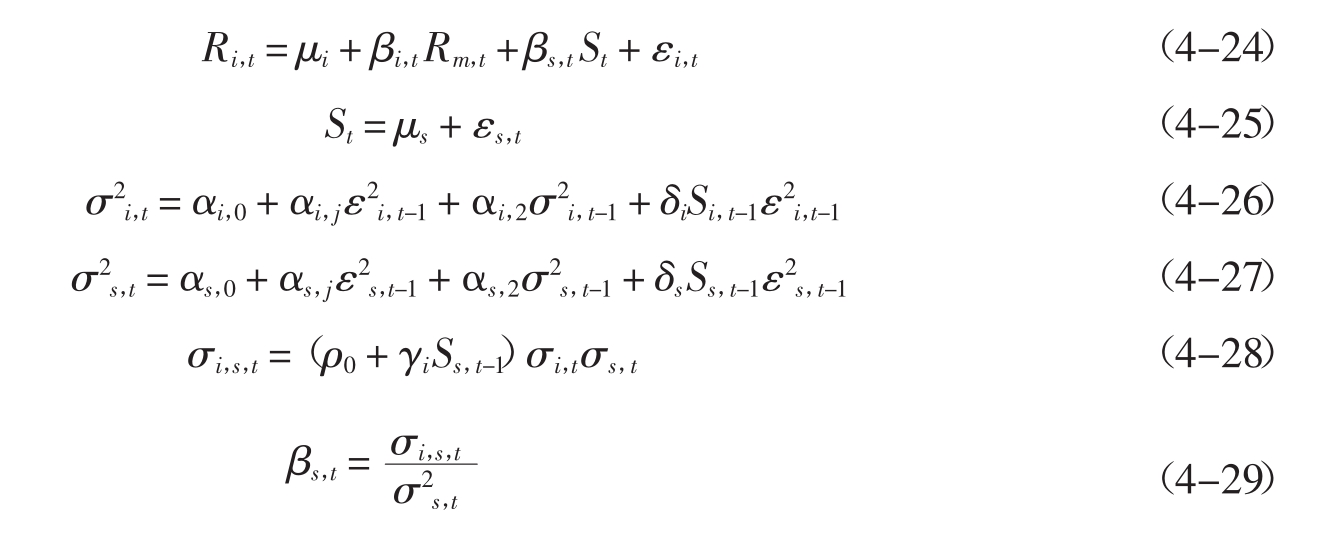
其中，i和s分别代表i资产或组合的回报和汇率变化，μ_i、μ_s分别表示条件均值，σ²_i，t、σ²_s，t、σ_i，s，t是时变的方差协方差矩阵。公式（4-26）和公式（4-27）设定了经过δ_iS_i，t-1ε²_i，t-1和δ_sS_s，t-1ε²_s，t-1项调整的遵循标准向量的GARCH（1，1）过程的股票回报和汇率变化的条件方差，如果ε_j，t-1＜0，则有S_j，t-1=1，否则为零，其中j=i，s。这些设定是为了捕捉条件方差的不对称，根据公式（4-26）和公式（4-27），正的创新的贡献等于α，负的创新的贡献等于α+δ，可以用

_{j，1j，1j，1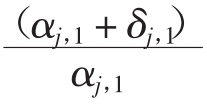}来衡量不对称效应。公式（4-28）在考虑汇率升值和贬值的不对称效应的情况下设定了协方差，如果λ_i为正且在统计上显著，则协方差在本币升值时更高一些。该方法将时变的影响系数与时变的方差协方差矩阵同时估计，提高了估计效率。该模型的实证研究表明，就以规模和产业为基础的投资组合而言，平均的时变影响系数在统计上是显著的，汇率变动对那些大公司和技术行业的公司影响较小。

2.公司在面临大的或小的汇率波动时存在行为差异

许多学者认为，公司不仅在本币升值或贬值期间采取不同的行为，在大的和小的汇率波动面前也会有行为差异。Baldwin（1988）指出当市场进入成本无法收回时，大的汇率波动能引起滞后效应。假定汇率的大幅上升使得外国公司进入本国市场，由于存在沉没成本，即使汇率恢复到原来的水平外国公司也不会离开该国市场。实证研究方面，Di Iorio和Faff（2000）认为公司价值会对大的和小的汇率波动做出不对称的反应，他使用了与Fabozzi和Francis（1977）相同的月度分析方法，非线性和不对称假设在实证分析中是以虚拟变量的形式出现的，时间序列数据是根据其标志和汇率变动的重要性进行分段的，该研究还调整了β系数以改变市场条件，如牛市和熊市的变化等。Muller和Verschoor（2004c）建议将模型建立在一种简单的假设基础上，即股票回报对汇率的反应存在两种状态，从一种状态转换到另一种状态是由汇率波动的幅度来触发的。他们认为在估计股票回报和汇率的关系时，将不对称效应引入进来会增加汇率变动影响的显著性并证明了量上的不对称变化比符号的不对称更为重要。

4.2.4.2　非线性设定

尽管多数学者认为汇率变化对股票市场的影响是不对称的，但股票回报对汇率的非线性反应迄今为止还没有引起充分的重视。有些学者认为非线性设定是不合适的，但Levi（1994）、Booth（1996）从理论角度对汇率对股票市场影响的非线性设定进行了探讨，Levi（1994）认为特殊的保值策略的应用和一些保值工具的非线性盈利结构将导致汇率和公司价值之间的非线性关系。Booth（1996）讨论了套期活动的交易成本及其对公司利润方程的不对称影响，并假定汇率的影响是非线性的和不对称的，他认为这可能是以往的研究线性设定无法揭示存在显著的汇率敏感性的原因。

实证研究中，Bartram（2004）建议进行凸的回归设定，即允许股票价格对正向和负向汇率变动有不同的反应。他在对德国490个非金融贸易公司的研究表明：凸的双曲线或者是立方方程有利于提高汇率影响的显著性，从而支持了非线性的模型形式。但是非线性设定既没有坚实的理论基础，又无法为股票回报和汇率波动之间的显著联系提供强有力的实证证据。

总之，从汇率对股票市场影响的研究方法的发展来看，对于宏观经济变量的引入及其与汇率之间的多重共线性问题的解决有利于汇率对股票市场影响的精确衡量，但是该领域目前仍然存在一些有待解决的问题。首先，汇率和市场因素的设定方面，迄今为止还没有发现最适于揭示汇率对股票市场影响的汇率形式和市场组合；其次，汇率影响的时变性引发的观测频率的选择方面，实证研究仍然没有发现最适于揭示该影响的观测频率。最后，模型的非线性的形式及其理论依据仍然有待进一步论证。

【注释】

[1]在使用Jorion的公司剩余外汇风险暴露的概念时必须谨慎。假定j国所有的公司都受到美元贬值的负向影响，Jorion模型中考虑的市场风险因素是j国全部市场回报，Jorion估计过程无法证明j国的任何公司存在显著的剩余风险暴露，尽管j国的股东价值实际上受到影响(Glaum,M.,Foreign exchange risk management in German non-financial corporations empirical analysis.In:Frenkel,M.,Hommel,U.,Rudolf,M.(Eds.),Risk Management Challenge and Opportunity.Springer,Berlin,2000,373-393)。

[2]该研究在第一步的分析中得到的是公司时变的外汇风险暴露，在第二步估计时作者通过使用面板数据和SUR(近似无关回归)技术对传统方法进行了改进。

[3]为了从市场因素中分离出汇率波动的效应，该研究将市场因素与其他作为解释变量的宏观经济变量进行正交化处理，将不能被其他因素解释的市场风险因素作为剩余市场因素引入模型。

[4]因为美国股票市场在整个世界中所占的份额较大，因此，回报率采用的是美元形式。