投资项目决策的基本方法

第三节　投资项目决策的基本方法

对投资项目进行评价时，所采用的指标主要分为两类：一类是非贴现指标，即没有考虑资金时间价值因素的指标；另一类是贴现指标，即考虑了时间价值因素的指标。根据评价指标的类别，投资项目决策评价的方法也被分为贴现决策评价方法和非贴现决策评价方法。常用的非贴现评价方法有投资回收期法和平均报酬率法，贴现评价方法有净现值、获利指数和内含报酬率等。下面就分别介绍这些方法。

一、投资回收期法

投资回收期（Payback Period，PP），是指投资引起的现金流入累计与投资额相等所需要的时间，它一般以年为单位，表示收回投资所需要的年限，回收期越短，方案越有利。投资回收期法是一种使用很早很广的投资决策方法。

投资回收期的计算，因每年的营业净现金流量是否相等而有所不同。如果每年的营业净现金流量（NCF）相等，则投资回收期可以用下列公式计算：

如果每年的净现金流量不相等，那么，计算投资回收期要根据每年的年末尚未收回的投资额加以确定。

例如，对于前例5-1中的方案A，每年的净现金流量相等，则其投资回收期可以计算为：

方案A投资回收期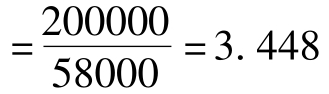（年）

而对于方案B，由于每年的净现金流量不相等，则需要计算每年年末尚未收回的投资额，计算过程如表5-3所示。

表5-3　投资回收期计算表　　单位：元

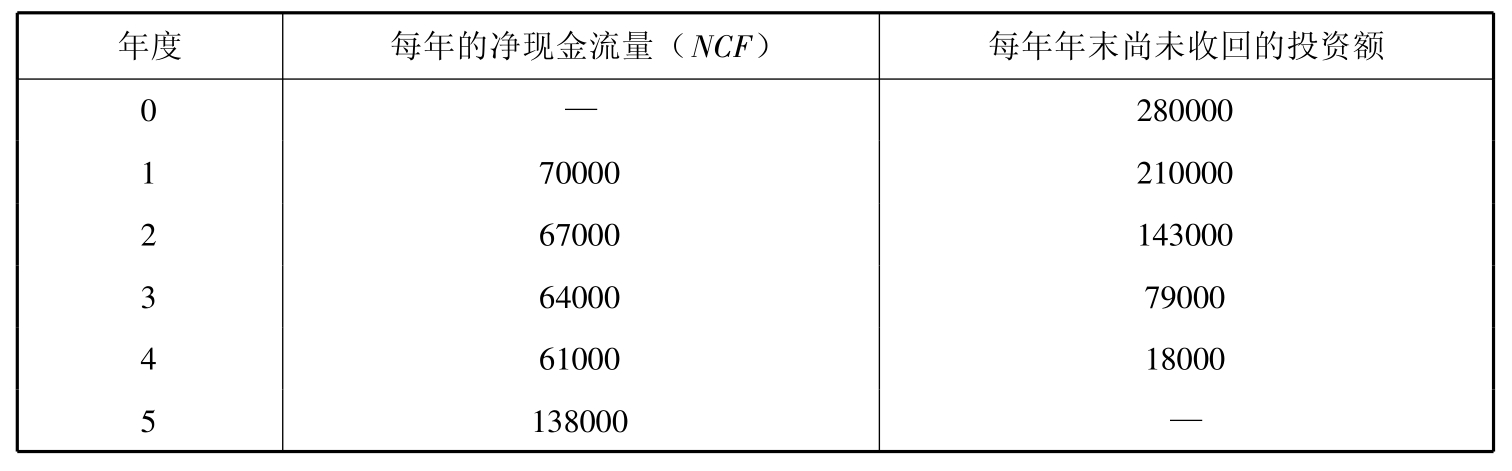
从表5-3中可以看出，到第4年年末，尚有18000元投资未收回，方案B的投资回收期可以计算如下：

方案B投资回收期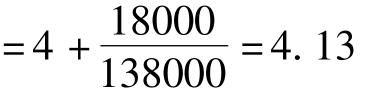（年）

从本指标看，方案A的投资回收期比方案B要短，因此，仅从本指标的角度考虑，应该把方案A作为优先选择的方案。

投资回收期法计算简便，并且容易被决策人所正确理解。它的缺点在于未充分考虑到资金的时间价值，并且没有考虑回收期期满后的项目收益。事实上，有战略意义的长期投资往往是早期的收益较低，而中后期的收益较高。因此，仅仅利用投资回收期法进行决策往往会导致企业优先考虑急功近利的项目，而放弃较为长期的成功项目。过去，投资回收期法是一种投资方案评价的最常用的方法，而现在，这种方法只能作为一种辅助方法来使用。

二、平均报酬率法

平均报酬率（Average Rate of Return，ARR）也称为平均收益率，是指投资项目寿命期内平均的年投资报酬率。平均报酬率有多种计算方法，其中最常见的计算公式为：

仍以例5-1中的数据为例，来计算其平均报酬率。

方案A的平均报酬率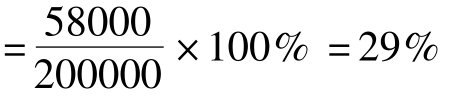

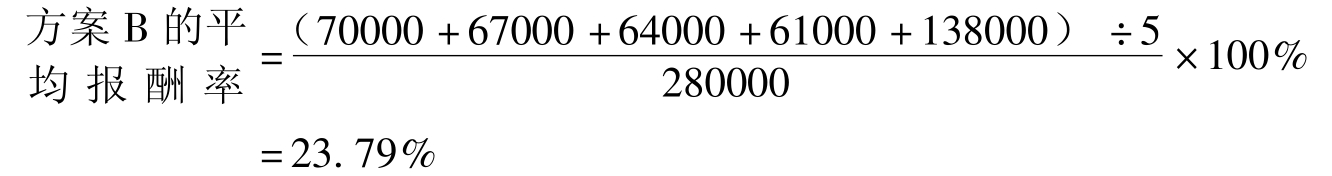
在计算平均报酬率时，也可以采用会计报表上的利润数据。在进行决策前，首先应该确定一个企业要求达到的平均报酬率。这样，在决策时，计算的平均报酬率只要高于必要的平均报酬率，则方案可行。而在有多个方案的互斥选择中，则应选择平均报酬率最高的方案。因此，从本指标的角度看，应选择平均报酬率水平较高的方案A作为优先的选择方案。

平均报酬率法计算简便，应用范围很广。但是，其缺点是未考虑到资金的时间价值，把不同时间的现金流量的价值看成是一样的，这样容易导致错误的决策。

投资回收期法和平均报酬率法是静态的投资决策方法，均未考虑到资金的时间价值因素。在决策中，这两种方法往往只能作为项目方案选择的辅助方法。

三、净现值法

所谓净现值（Net Present Value，NPV），是指特定方案未来现金流入量的现值与未来现金流出量的现值之间的差额。按照这种方法，所有的未来现金流入和流出量都要按照预定的贴现率折算为它们的现值，然后再计算它们的差额。如果净现值为正数，则贴现后的现金流入大于贴现后的现金流出，表示该项目的投资报酬率大于预定的贴现率；如净现值为零，则表示贴现后的现金流入等于贴现后的现金流出，表示该项目的投资报酬率相当于预定的贴现率；如果净现值为负数，则贴现后的现金流入小于贴现后的现金流出，表示该项目的投资报酬率小于预定的贴现率。净现值的计算公式如下：

式中：n表示投资涉及的年份；I_k表示第k年的现金流入量；Q_k表示第k年的现金流出量；i表示预定的贴现率（资本成本或者企业要求的报酬率）。

若项目为一次性投资，则净现值的计算公式也可以表示为：

式中：C表示一次性的初始投资额；NCF_k表示第k年的净现金流量。

仍以例5-1中的数据为例，这里假设预定的贴现率为10%。对于方案A来说，由于每年的净现金流量相等，则其净现值可以计算为：

方案A的NPV= NCF×PVIFA_i，n-C

　　　　　=58000×PVIFA_10%，5-200000

　　　　　=58000 ×3.791-200000

　　　　　=19878（元）

而对于方案B来说，由于每年的净现金流量不相等，则其净现值可以计算为：

方案B的净现值NPV=70000 ×0.909+67000 ×0.826

　　　　　　　　+64000 ×0.751+61000 ×0.683

　　　　　　　　+138000 ×0.621-280000

　　　　　　　　=14397（元）

在两个方案中，其净现值均为正数，说明这两个方案的报酬率均大于10%。如果企业的资金成本或者要求的必要报酬率就是10%，则说明这两个方案都是有利的，因而是可以接受的。净现值法所依据的原理是：假设预计的现金流入在年末肯定可以实现，并把原始投资看成是按预定贴现率借入的，则当净现值为正数时，表明偿还本息后该项目还有剩余的收益，所以项目是可行的；当净现值为0时，表明偿还本息后一无所获；而当净现值为负数时，表明该项目的收益不足以偿还本息，则项目不可行。由此可见，净现值的经济含义是投资方案的贴现后的净收益。

当只有一个备选方案时，如果用净现值法进行采纳与否的决策，则如果净现值大于0就应该采纳，如果净现值小于0就不应该采纳。在有多个备选方案的互斥选择决策中，应选用净现值为正值中的最大值。在本例中，两个方案的净现值均大于0，所以均可行。但是，由于方案A的净现值更大，因此，从本指标的角度看，应选择方案A作为优先的方案。

显然，在应用净现值法进行投资项目决策时，主要问题是要确定一个合适的贴现率。一般来讲，贴现率的确定有两种办法：一是根据项目所筹集资金的资金成本来确定；二是根据企业要求的最低资金利润率来确定。对于前一种办法，由于资金成本的计算比较困难，就限制了其应用的范围，而后一种办法则可以根据资金的机会成本来确定。所以，在一般情况下，用可以获得的报酬率来确定贴现率，是一种比较简洁有效的办法。

净现值法的优点是，考虑了资金的时间价值，能够反映各种投资方案的净收益，因而它具有广泛的适用性，在理论上也比其他方法更加完善，净现值法是投资决策评价中的最基本的方法。但是，净现值法也有一定的缺点。首先，它不能揭示各个投资方案本身的实际可达到的报酬率真正是多少？其次，当几个投资项目或几个方案的初始投资额不一致时，简单地比较它们之间净现值的大小显然是不合适的。这两个缺点分别可以用下面的两个指标内含报酬率和获利指数来补充。

四、获利指数法

获利指数（Profitability Index，PI）又称为现值指数、现值比率或贴现后收益—成本比率；它是指未来每年的现金净流量的现值与初始投资的现值的比率。当初始投资为一次性投入时，其计算公式可以简化表示为：

按照上面的计算公式，就可以分别计算得出例5-1中两个方案的获利指数：

方案A的获利指数PI=58000 ×3.791 ÷200000=1.10

方案B的获利指数PI=（63630+55342+48064+41663

　　　　　　　　　　+85698）÷280000

　　　　　　　　　=1.05

在应用获利指数法进行决策时，如果只有一个备选方案的采纳与否决策，只要获利指数大于或等于1，则表明其报酬率达到了预定的贴现率，就应该采纳；否则就应该拒绝。在有多个方案的互斥选择决策中，应采用获利指数大于1最多的投资项目。

在这里，两个方案的获利指数均大于1，表明这两个方案均可行。但是，方案A的获利指数较大，所以，从本指标来看，应选择方案A作为优先的方案。

获利指数法的优点是：考虑了资金的时间价值，能够真实地反映投资项目的盈亏程度。由于获利指数是用相对数表示的，所以，它有利于在初始投资额不同的投资方案之间进行比较。

作为评价方案的一个指标，获利指数可以看成是1元原始投资可望获得的现值净收益，它是一个相对数指标，反映了投资的效率；而净现值指标则是一个绝对数指标，反映了投资的效益。

五、内部报酬率法

内部报酬率（Internal Rate of Return，IRR），又称为内含报酬率、内含收益率；它是指能够使未来现金流入量现值等于未来现金流出量现值的贴现率，或者说是使投资方案净现值为零时的贴现率。

净现值法和获利指数法虽然考虑了资金的时间价值，可以说明投资方案高于或低于某一特定的投资报酬率，但并不能够真正揭示方案本身可以达到的具体的报酬率是多少。内部报酬率就是根据方案的现金流量计算所得到的方案本身的实际投资报酬率。

如果投资项目每年的现金净流量相同，则内部报酬率的计算相对比较简单。这里以例5-1中的方案A为例进行说明。在这里，要计算使该方案的净现值为零时的贴现率，我们有：

方案A的NPV= NCF×PVIFA_i，n-C

　　　　　=58000×PVIFA_i，5-200000=0

则有：PVIFA_i，5=200000 ÷58000=3.4483

这里要利用插值法进行计算。查年金现值系数表，n=5时，与3.4483相邻近的年金现值系数在12%～14%之间，则该方案的内部报酬率可以用插值法计算如下：

从而可以有：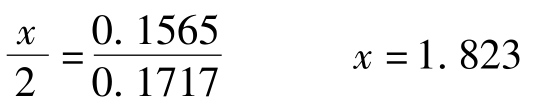

方案A的内部报酬率=12%+1.823%=13.823%。

对于每年的净现金流量不相等的情况，则相对比较复杂。通常需要采用“逐步测算法”。首先估计一个贴现率，用它来计算方案的净现值；如果净现值为正数，则说明方案本身的报酬率超过估计的贴现率，应提高贴现率后进行进一步测试；如果净现值为负数，则说明方案本身的报酬率低于估计的贴现率，应降低贴现率后进一步测试。经过如此多次反复测试，可以找到净现值由正到负并且比较接近于零的两个贴现率。再根据这两个邻近的贴现率，利用插值法计算出该方案的实际内部报酬率。

这里以例5-1中的方案B为例，来说明每年的净现金流量不相等情况下的内部报酬率的计算过程，如表5-4所示。

表5-4　每年的净现金流量不相等情况下内部报酬率的计算　　单位：元

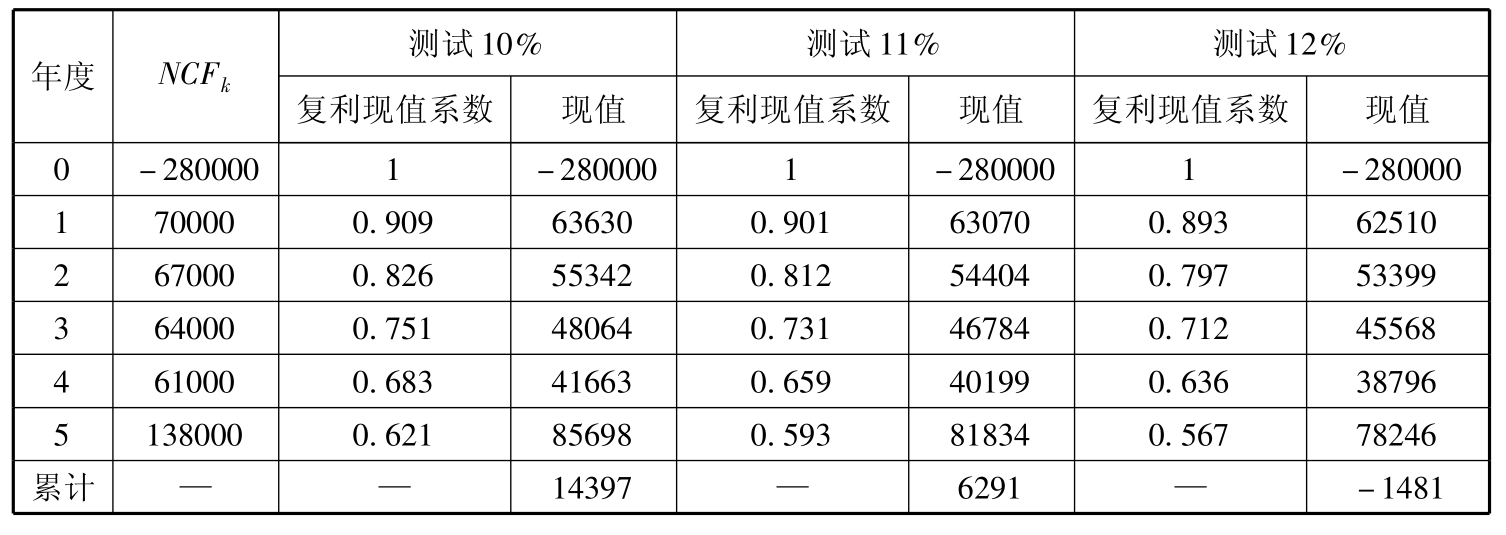
在表5-4中，先按10%的贴现率进行测算。净现值为正数；接着，再把贴现率提高到11%，进行第二次测试，净现值仍然为正数，说明内部报酬率仍然大于11%；然后再把贴现率提高到12%进行测算，得到的净现值为负数。这说明该项目的内部报酬率一定在11%～12%之间。现在，可以用插值法计算内部报酬率如下：

从而可以有：

因此，该方案的内部报酬率为11%+0.809%=11.809%。

从内部报酬率指标的角度看，A方案的内部报酬率要大于B方案的内部报酬率，从而A方案要优于B方案。

内部报酬率方法的优点在于考虑了资金的时间价值，同时也反映了投资的真实报酬率，但是，这种方法的计算过程比较复杂，特别是对于每年的净现金流量不相等的投资项目，一般要经过多次测算才能得到最终的结果。当然，在内部报酬率的计算过程中，可以借助于计算机工具，通过事先编制好的程序，直接计算得出特定现金流量条件下的内部报酬率。