高速公路是搏命者的天下,你可要当心。
如果碰巧捡到了点什么,那你一定要收好了。
鲍勃·迪伦(Bob Dylan)
与上帝赌博
艾克开着他华丽的新保时捷跑车撞到了电线杆上,不幸意外身亡。可是在天堂里,艾克是幸福的:他可以一直玩游戏了,其实艾克骨子里就是一个赌棍。
一天,上帝他老人家亲自邀请艾克玩一个非常奇特的游戏:上帝让他写下一个16位数字。上帝要掷骰子,那种天堂里特有的20面的骰子。与我们凡间通常所见的6面骰子不一样,这个骰子有20个面,从0~9的10个数字每个出现两遍。上帝解释道,他要掷16次骰子,把每次掷的结果依次写下来形成一个16位的数字。如果上帝和艾克写的都是同一个数字——也就是说,所有数字顺序相同,那么,上帝就赢了;如果数字不完全相同——假设有任何一位数不对,那么艾克就赢了。
上帝开始摇。他掷出的第一个数是“4”,这与艾克所写数字的第一位恰好相符,艾克的数字是“4 715 031 495 526 312”。上帝能恰好摇出同样的数,让艾克感到很惊讶,因为这概率只有1/10,但他相信,第二个、第三个肯定就不会一样了,因为上帝连续掷出两个数字都相符的概率只有1/100。
上帝再次摇骰子,然后第三次,他分别掷出一个“7”和一个“1”,又对上了!他继续掷,这下艾克可是目瞪口呆了:上帝掷出的所有数字都对了。这一概率是一亿亿分之一,上帝怎么可能会赢呢?
艾克有点儿生气(在天堂里,人不可能火气太旺),他问,像这样根本不可能的事是怎么发生的?上帝圣明地答道:“只有我才可能赢,因为我是无所不知、无所不能的,但是,你一定也曾听说过,我不喜欢掷骰子。”
说完,空中出现四个大字——“禁止赌博”。艾克愤怒了(当然,只是一点点儿),他不仅输了这场游戏,还失去了赌博的权利。
到现在为止,你已经学到了有关粒子物理学的大量知识,并了解了物理学家建立标准模型的许多理论元素。在解释许多不同的实验结果时,标准模型发挥了异常强大的作用,但是,它的基础是极不稳定的,这基础本身就是一个意味深长的谜题,而它的谜底几乎必然会引发对物质基本结构的新的认识。本章我们就将探索这一谜题,也就是物理学家所说的等级问题(hierarchy problem)。
这一问题并非指标准模型预言与实验结果不符,关于电磁力、弱力、强力的质量和电荷都已得到了精确验证;在CERN、SLAC和费米实验室进行的实验,也都证实了标准模型对于已知基本粒子相互作用和衰变速度的预言;标准模型中强力的强度也已无神秘之处;而且,它们之间的关系还启发人们想到了一个潜在的大统一理论的观点;再者,希格斯机制也完美地解释了真空怎样打破弱电对称,使W、Z规范玻色子以及夸克和轻子获得质量。
等级问题
为什么希格斯粒子的质量,以及由此带来的弱力规范玻色子的质量如此微小?等级问题告诉我们,在推想极端高能的物理过程之前,我们至少还有一个低能的问题迫切需要解决。
但无论表面多么其乐融融的家庭,如果深入观察,你总会发现紧张的暗流在涌动。尽管表面呈现的是一幅和谐、幸福的景象,但暗地里却隐藏着毁灭性的家族秘密。标准模型就有这样一个隐痛。如果你不加批判地认为,电磁力强度、弱力强度和规范玻色子都采用实验测得的值,那么所有东西都会符合预言。但我们很快会看到,质量参数(决定基本粒子质量的弱力级质量)虽然已被精确测量,但它比物理学家根据一般理论思考得出的质量要小16个数量级。任何物理学家要依据高能理论推算弱力级能量(从而推算所有的粒子质量),都会发现它彻底错了,质量似乎是无中生有的。这一谜题——等级问题,是我们对粒子物理学认识的一个巨大漏洞。
我在引言里把等级问题解释成引力为何如此微弱的问题。但现在我们看到,这一问题还可以阐释为:为什么希格斯粒子的质量,以及由此带来的弱力规范玻色子的质量如此微小?这些质量要与它们的测量值相符,标准模型必须加进一个附加参数,而这个参数就如有人要随机地掷出一个16位数字,结果必须与艾克的数字恰好相符一般不可能。尽管标准模型有许多成功之处,但它却要依靠这一荒谬、不合情理的参数,才能得出已知基本粒子的质量。
本章解释了这一问题,也解释了为什么我和多数粒子理论学家都认为它那么重要。等级问题告诉我们,无论是什么使得弱电对称产生破缺,它都会比第10章呈现的两个希格斯场的例子更为有趣。所有可能的解决方法都会涉及新的物理原理,而答案将可能引导物理学家发现更基本的粒子和定律。找到是什么发挥了希格斯场的作用并打破弱电对称,会给我们展现一些新的、最为丰富的物理现象,或许在我有生之年,它们就会得到确定。几乎可以肯定的是,在大约1 TeV的能量上,一定会出现新的物理现象。检验各种假说的实验也已准备就绪,不出10年,不论有什么实验发现,我们对基本物理定律的认识,都将发生巨大的改变。
等级问题告诉我们,在推想极端高能的物理过程之前,我们至少还有一个低能的问题迫切需要解决。在过去大约30年里,粒子物理学家一直在探寻一种理论结构,能够预言和维护弱力级能量,这是弱电对称破缺相对较低的能量。我们许多人都认为,对于等级问题必会有一个解决方法,它将提供最好的线索,告诉我们超越标准模型会有什么。很快我将讲述一些理论,要理解这些理论的动机,我们首先要简单地了解一下这个虽然专业却很重要的问题。对解决方法的探求已引导科学家们开始研究一些新的物理概念,如后面几章探讨的那些概念,而问题的解决几乎必然会修正我们现在的观点。
在探讨等级问题的一般形式之前,我们首先来看大统一背景之下的等级问题,这比较好理解,而且,我们正是在大统一理论里首先认识到了这一问题。然后,我们要在更大(也更为普遍)的背景之下来看这个问题,看它为什么会最终归结为引力比其他已知力更微弱的问题。
等级问题,大统一理论里的依赖性问题
假设你去看望一位个子很高的朋友,他的身高大约是1.95米,而你发现他的同胞兄弟却只有1.5米,你是不是会感到非常惊讶呢?你会以为,朋友和他的兄弟有着相似的遗传基因,个子也应该差不多高。现在再设想,事情可能更离奇:你到了朋友家里,发现他哥哥的身高比他要高10倍或是矮10倍。这才真的会让人感到无比奇怪呢!
除非有充分的理由,我们并不认为所有的粒子都会有着相同的属性,所以我们通常认为,经受同样力的粒子性质也应是相似的,例如,我们认为它们的质量也应该差不多。就如你有足够的理由认为同胞兄弟身高应该不会差很多一样,粒子物理学家也有充分的科学依据,期待粒子质量在同一理论里也应是相似的,如在大统一理论里。但是,大统一理论里的质量却绝非相同:即便是经受相似力的粒子,其质量也有着巨大的差异,这可不是10倍的差别:它们之间质量的差超过了10万亿倍。
大统一理论的问题在于:尽管打破弱力对称的希格斯粒子必须很“轻”,大致应是弱力级质量,但大统一理论却提出一个对应的通过强力与其他粒子发生相互作用的希格斯粒子。大统一理论的这个新粒子却必须极重,大约是大统一级质量。换句话说,这两个本应由一种对称(大统一力的对称)相联的粒子,其质量却有着天壤之别。
在大统一理论里,这两个不同却互相关联的粒子必须同时出现,因为在高能量上弱力和强力应是可以互换的,这是大统一理论背后的整个观点——所有的力都是一样的。因此,当强力和弱力统一起来时,经受弱力的所有粒子,包括希格斯粒子,都必须伴有另一个经受强力的粒子,并且与原来的希格斯粒子有着类似的相互作用。但是,这一与希格斯粒子相关联的、经受强力的新粒子,却存在着一个大问题。
这个与希格斯粒子为伴的强荷粒子能同时与夸克和轻子产生相互作用,因此能使质子衰变——甚至比大统一理论预言的速度还要快。要使质子发生衰变,强相互作用的粒子必须在两个夸克和两个轻子之间进行交换;为避免过快衰变,它们则必须极重。而目前质子的寿命限制告诉我们,强荷的希格斯粒子伙伴,如果自然界中存在的话,其质量必须接近于大统一标度的质量,大约为1 000万亿GeV。假使这一粒子存在却没有这么重,那么不等你看完这句话,你和这本书就都将灰飞烟灭。
但是,我们已经知道,弱荷的希格斯粒子必须很轻(大约250 GeV)才能使弱规范玻色子质量与实验测得的质量相符。这么一来,实验设定的限制告诉我们,希格斯粒子质量一定与其经受强力的伙伴粒子质量有着天壤之别。在一个统一的理论里,假定与弱荷希格斯粒子有着相似相互作用的强荷希格斯粒子必须具有不同的质量,否则这世界就不会是我们看到的样子。这两个质量间的巨大差异——一个是另一个的10万亿倍,真的难以解释,尤其是在一个统一的理论里,不论强荷粒子还是弱荷粒子,都假定有着相似的相互作用。
在大多数统一理论里,要让一个粒子重而另一个粒子轻,唯一的办法就是引进一个巨大的附加参数,任何物理原理都不会预言这么大的质量差异。精心选择一个参数是使它有效的唯一办法,而这一数字的精确值必须达到13位,否则,要么质子会快速衰变,要么弱力规范玻色子的质量就会变得很大。
粒子物理学将这一必要的附加参数称作微调,微调就是为了得到期望的精确值而对参数进行的调整。选择“调”这一词,就像是为了让钢琴敲出正确的音符而对琴弦进行的调试。如果你想让一个只有几百赫兹的音频达到13位数的精确度,那么你监听的时间则必须达到100亿秒,即1 000年。13位数的精确度实在是千年难遇的。
有关微调的比喻,我还可以举出其他一些例子,但我肯定它们听起来都缺乏真实性。例如,在一家大公司里,一人负责开支,一人负责收入,假设他们从来不曾交流和沟通,而到年底时,公司的支出应当恰恰等于收入——不可超过1美元,要不然这公司就会倒闭。是的,这个例子实在是太不切实际了。而它不可能切合实际,任何一个符合常理的情形都不会依赖于微调,没人会把自己的命运(或是企业的命运)悬在那几乎不可能发生的偶然巧合上。但是,几乎所有包含一个轻希格斯粒子的大统一理论,都存在这样的依赖性问题。如果一个理论的物理预言这么敏感地依赖于一个参数,那它根本不可能成为一个完善的理论。
但是,最简单的大统一理论要得到一个小质量的希格斯粒子,唯一的办法就是在理论里加进一个附加参数,大统一理论模型没有提供更好的方法。对于在四维中统一的大多数模型来讲,这是一个严重的问题,正因如此,许多物理学家,包括我自己在内,对力的统一都持怀疑态度。
而等级问题愈发严重:即便你不需要根本的解释,而乐于简单地假定一个粒子极轻而另一粒子极重,你还是会遇到所谓量子力学贡献(或简称量子贡献)带来的问题。这些量子贡献必须加在经典的质量之上,才能确定希格斯粒子在真实世界中的真正的物理质量,而这些贡献通常会远远大于希格斯粒子所要求的几百GeV的质量。
我先提醒一下,下一节里有关量子贡献的讨论,虽说是以虚粒子和量子力学为基础,却可能并不符合人的直观理解,所以不要尝试以经典的类比去想象,我们要思考的就是一个纯粹的量子力学效应。
对希格斯粒子质量的量子贡献
上一章我们讲到,通常一个粒子不会毫无妨碍地穿越空间,虚粒子时而出现,时而消失,因此影响了原本粒子的路径。量子力学告诉我们,对任何一个物理量,我们必须把所有这些可能路径的贡献都加进来。
我们已经看到,这些虚粒子的存在使得实验测得的力的强度对于距离的依赖完全符合预言。使得力对能量产生依赖的这一同类型的量子贡献,还会影响到质量的大小。但就希格斯粒子的质量来说,与力的强度不同,所以虚粒子的作用与实验对理论的要求似乎并不相符,它们似乎太大了。
因为希格斯粒子会与一些重粒子发生相互作用,它们的质量高达大统一级别,所以希格斯粒子所采取的路径包含了由真空中分裂的虚重粒子及其反粒子,希格斯粒子在其行驶途中会暂时地转化成这样一些粒子(见图12-1)。在真空中忽生忽灭的重粒子会影响希格斯粒子的运动,是它们导致了大量的量子贡献。

图12-1 在大统一理论中,重粒子对希格斯粒子质量的虚贡献。希格斯粒子会转变成虚重粒子(大统一质量),然后它们再转回成希格斯粒子。左边简图和右边费曼图都说明了这一过程。
量子力学告诉我们,如果要确定希格斯粒子实际拥有的质量,我们必须在那条没有虚粒子的路径上加进这些有着虚重粒子的路径。问题在于,包含了虚重粒子的路径导致的贡献,会使希格斯粒子达到大统一理论里重粒子的质量——比我们所需质量高13个数量级。所有这些来自虚重粒子的巨大贡献,都必须加到希格斯粒子质量的经典值上,产生的物理值还必须符合测量。如果要使弱规范玻色子的质量正确,这一值大约应是250 GeV。这就意味着,即便任一GUT质量贡献都要大至13个数量级,但当我们把所有这些巨大贡献加进质量时,最终的答案应该接近于250 GeV,如果有些贡献为正,则有些必然为负。哪怕只有一个虚重粒子与希格斯粒子发生作用,都会不可避免地出现问题。
如果像上一章那样,我们把虚粒子看作官僚机构的成员,那么,它们的职责就像美国移民局(INS)的员工一样,是为了拦截来自可疑人员的信件,而现在,他们却仔细地审查所有信件。本来是一个两层的系统,可以让一些信件快速通过,只拦截另外的一些,现在呢,所有信件都被同样对待。同样的道理,希格斯机制要求虚粒子“官僚”能够让有些粒子重,而让包括希格斯粒子的另外一些粒子轻,但是,就像工作热情过高的官员一样,包含虚粒子的量子路径对所有粒子的质量都有同等的贡献。因此我们期待所有粒子,包括希格斯粒子在内,都具有大统一标度的质量。
如果没有新的物理理论,那么解决希格斯粒子质量过大问题的唯一(且并不令人满意的)方法是:假设它的经典质量值会恰好抵消巨大的量子贡献(这样,经典值就有可能为负)。尽管单个的贡献都很大,但理论中决定质量的参数必须使所有的贡献相加起来的数值很小,这就是上节里我提到的微调。
这虽然可以想象,但要在现实中发生几乎是不可能的。这一问题不单单是加进一个参数稍作调整就能得到正确质量的问题,而是因为这一参数太大了,结果又要求无比精确:精确值少于13位则会导致结果完全错误。要明确的是,这一离奇的参数不同于精确测量的某个量,如光速。通常情况下,定性预言并不依赖于任何一个参数取什么特定的值。只有一个值能契合已测得的精确量,但即便一个参数稍有不同,世界也不会产生很大变化。也就是说,牛顿引力常数(它确定了引力强度)的值即使1%的误差,结果根本不会有什么太大的变化。
而在大统一理论里,参数的稍微一点变化足以彻底毁掉理论预言,不论定量的预言还是定性的预言。打破弱电对称的希格斯粒子的质量异常敏感地依赖于一个参数。对这个参数的几乎所有数值,大统一质量和弱力质量之间的等级分化都不会存在,因而也就没有依赖这个等级的结构和生命。即使这一参数仅出现了1%的偏差,希格斯粒子的质量也会变得很大,弱规范玻色子以及其他粒子的质量也都会大得多,而标准模型的结果也就根本不是现在这个样子了。
粒子物理的等级问题
上一节里,我们看到了一个很大的谜团:大统一理论的等级问题。而真正的等级问题更糟:尽管是大统一理论首先惊醒物理学家意识到了等级问题,但即使在没有GUT质量的粒子理论中,虚粒子仍会对希格斯粒子质量引发过大的贡献,甚至连标准模型都值得怀疑。
问题在于,将标准模型与引力结合起来的理论会包含两个差别极大的能量尺度。
一个是弱力能标,即250 GeV,在此能量上,弱电对称破缺。当粒子能量在此标度之下时,弱电对称破缺的效果是很明显的,弱规范玻色子和基本粒子都有质量。另一能量是普朗克能量,高达1019 GeV,比弱力能标大1016倍,即1亿亿倍。普朗克能量决定了引力作用的强度:牛顿定律说,强度与其能量的平方成反比。因为引力强度很小,普朗克质量(由E=mc2与普朗克能量相联)就会很大,巨大的普朗克质量就等同于极其微弱的引力。
到现在为止,普朗克质量还没有进入我们粒子物理学的讨论范畴。因为引力太过微弱,对大多数的粒子物理计算,它都可以忽略不计。但这正是粒子物理学一直想要解答的问题:为什么引力如此微弱,以至于在粒子物理计算里都可以忽略?等级问题换一种方法来问就是:为什么普朗克质量如此巨大?与粒子物理尺度相关的质量都不超过几百GeV,为什么普朗克质量却要大出1亿亿倍?
为方便比较,你可以想象两个低质量的粒子,如两个电子间的引力作用。这种引力吸引相比两个电子之间的斥力要弱1万亿亿亿亿亿倍,只有当电子的质量比实际再重100万亿亿倍时,这两种力才有可比性。而这是一个巨大的数字——就好比要把整个可见宇宙都填满曼哈顿岛,你所需要的岛的数量。
普朗克质量要远远大于电子以及我们所知的其他粒子的质量,这表明引力比其他已知力要微弱许多。但为什么在力的强度之间会有这么巨大的差异——或者,换句话说,为什么普朗克质量相比其他已知粒子的质量会如此巨大?
对粒子物理学家来说,普朗克质量与弱力质量之间的巨大差异达到1亿亿倍,这真的让人难以接受。这一数字,比从宇宙大爆炸起到现在经过的分钟数都要大;若在地球和太阳之间摆满玻璃球,它是所需玻璃球数量的1 000倍;如果用硬币来核算美国财政赤字,那么它就是这些硬币数量的100倍!为什么描述同一物理系统的两个质量会有如此巨大的差异?
如果你不是物理学家,无论这些数字大得有多离奇,你可能也感觉不到这一问题本身有多重要,毕竟,并不是所有事情都是我们能够解释的,也许这两个质量的差异我们也找不出什么原因。但是,实际情况更糟:不能解释的不仅仅是巨大的质量比例问题,我们在下一节会看到,在量子场论里,所有与希格斯粒子发生相互作用的粒子都会参与一个虚过程,使希格斯粒子质量的值增大到普朗克质量,高达1019 GeV。
事实上,任何一个诚实的物理学家,假设他知道引力的强度,而对弱力规范玻色子已测得的质量一无所知,如果你请他用量子场论来估算希格斯粒子的质量,他预言的希格斯粒子质量(由此也得出弱规范玻色子质量)也不会大出1亿亿倍。这就是说,他会由计算得出结论,普朗克质量与希格斯质量(或者说由希格斯粒子质量来确定的弱力级质量)之比更接近于1,而不是1亿亿!他所计算的弱力质量会接近于普朗克质量,这样,所有粒子都将变成黑洞,而我们了解的粒子物理知识也将不复存在。尽管无论对弱力质量还是普朗克质量的数值,他都没有先验的预期,但他可以用量子场论估算二者的比值——而他必会大错特错。显然,这里存在着一个巨大的差别,下一章我们就解释其原因。
高能量的虚粒子
普朗克质量进入量子场论计算的原因非常微妙。正如我们所见,普朗克质量决定了引力强度,根据牛顿定律,引力与普朗克质量的值成反比。而引力如此微弱则告诉我们,普朗克质量非常巨大。
通常来讲,在做粒子物理学方面的预言时,我们可以忽略引力,因为对于一个质量大约为250 GeV的粒子,引力作用完全是可以忽略不计的。如果你真的需要解释引力效应,你可以系统地兼容它们,但通常不值得去费事。在后面的几章里,我会给出一个全新的截然不同的图景,其中高维引力非常强大,不能被忽略,但在传统的四维标准模型里,忽略引力是惯常而合理的做法。
但是,普朗克质量还有另外一个作用:在一个可靠的量子场论的计算里,它是虚粒子所具备的最大质量值,如果粒子携带的质量大于普朗克质量,计算将不再可信,广义相对论也不再可信,只能由一个更为综合的理论(如弦理论)来代替。
可如果粒子(包括虚粒子)质量小于普朗克质量,惯常的量子场论仍然适用,依据量子场论的计算应当也是可信的。这就意味着,即使计算涉及了质量几乎高达普朗克量级的虚顶夸克(或任何其他虚粒子),结果也是可靠的。
这里的等级问题是,来自极高质量的虚粒子对希格斯粒子质量的贡献会大至普朗克量级,比我们需要的希格斯粒子质量,即能给出正确的弱力质量和其他基本粒子质量的质量,要大出1亿亿倍。
设想一个路径,如图12-2所示,在这一路径中,希格斯粒子将转化成一对虚顶夸克-反顶夸克,我们会看到,对于希格斯粒子的质量,这一贡献太大了。事实上,与希格斯粒子发生作用的任何类型的粒子都可能会是一个虚粒子,而其质量[51]达到普朗克量级,所有这些可能路径的结果就形成了对希格斯粒子质量的巨大贡献。而希格斯粒子必须要远小于这一质量。
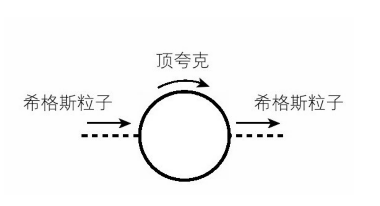
图12-2 虚顶夸克和虚反顶夸克对于希格斯粒子质量的贡献。希格斯粒子可以转化成一个虚顶夸克和一个虚反顶夸克,它们会对希格斯粒子的质量产生巨大的贡献。
在目前这种状态下,粒子物理学就像是一个太过高效的“涓滴式”理论。在经济学里,财富的等级分化并不难达到。利益均沾的涓滴经济学从来就没能增加穷人的财富,更不消说提高上流社会的经济水平了。但在物理学里,财富的转化却太有效了。如果一个粒子质量很大,量子贡献则会告诉我们所有基本粒子的质量都应该很大,结果所有的粒子都具有质量。但我们由测量得知,在我们的世界里,高质量(普朗克质量)和低质量(粒子质量)是同时存在的。
如果不对标准模型进行修正或推广,粒子物理只有通过神奇的经典质量值才能使得希格斯粒子获得小质量,而这一神奇值必须极大(且有可能是负值)才能完全抵消巨大的量子贡献。所有的质量贡献相加必须等于250 GeV。
正如我们前面探讨的大统一理论一样,要做到这些,质量必须是一个经过微调的参数,而这一微调参数必须极大且精确得惊人,才能使希格斯粒子恰好得出一个很小的最终质量。来自虚粒子的量子贡献和经典贡献两者之间必有一个是负值,而且两者量级几乎相同。正、负两个数值都要达到16个数量级,相加起来必须得到一个很小的数。这一微调要求的精确度必须达到16位,比你要让一支铅笔的尖朝下立起来所需做的微调要求还要高,这就像让一个人随机选择,在那场游戏里打赢艾克一样。
要保证希格斯粒子质量很轻,那么标准模型就需要微调。粒子物理更希望一个模型不需要涉及这种高要求的微调,尽管作为无奈之举,我们可能会做一些微调,但我们讨厌这样。微调几乎是一种耻辱,反映了我们的无知。虽然不太可能的事常会发生,但你越想它发生,它却越少发生。
等级问题是标准模型所面临的最为迫切的问题,但让我们乐观一点来看:等级问题提供了一个线索,让我们去发现究竟是什么扮演着希格斯粒子的角色并打破了弱电对称。取代两个希格斯场理论的任何一个理论,都应该自然地包括或预言一个很低的弱电质量——否则这一理论根本不值得考虑。许多潜在理论都能与我们看到的物理现象和谐相容,但很少有理论触及等级问题,并以令人信服地避免了微调的方式把轻质量的希格斯粒子包括在内。
将力统一起来的任务虽然艰巨,但这一来自高能物理的理论引人入胜、充满了诱惑;而解决等级问题,是我们必须完成的一项实实在在的任务,它将激励着低能量研究领域的进步。使得这一挑战愈发振奋人心的是,任何解决等级问题的理论都会产生可由LHC测量的实验结果。实验者们期待,能在LHC的实验里找到质量在250~1 000 GeV之间的粒子。如果没有其他粒子,也就没有办法解决这一问题。我们很快会发现,解决等级问题的实验结果有可能是超对称伙伴,也有可能是我们将在以后讨论的在额外维度航行的粒子。
●尽管我们都知道希格斯机制赋予粒子质量,但体现希格斯机制的最简单的已知例子只有通过一个巨大的附加参数才会奏效。在这一简单的理论里,规范玻色子和夸克的质量要比其实际质量大出1亿亿倍。等级问题问的就是,为何事情并非如此?
●等级问题起因于弱力质量与巨大的普朗克质量之间的差异(见图12-3),后一质量对引力非常重要——其巨大的质量值告诉我们引力非常微弱。因此,换一种方式来问等级问题就是:“引力为什么这么微弱,要远远地小于其他三种已知力。”
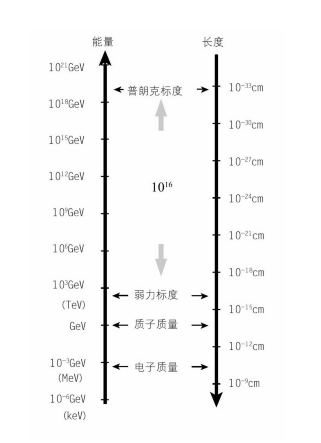
图12-3 弱力质量与普朗克质量的差异。等级问题即为什么普朗克级能量要远远地大于弱力级能量。
●任何解决等级问题的理论都可以用实验来验证,因为它们对以高于弱力能标的能量运行的对撞机都有实验意义。大型强子对撞机很快就将探索这样的能量。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















