位置矢量与速度加速度的关系

为了写出矢量形式的牛顿定律，我们只需要再走一步，接着定义加速度矢量就够了。这一步就是速度矢量的时间导数，容易证明它的分量是x,y和z对时间i的二阶导数

利用这个定义，牛顿定律就可以按这样的方式写出：

或者

于是，证明在坐标旋转下牛顿定律的不变性这个问题就是：证明a是一个矢量；我们刚刚做了这个证明。证明F是一个矢量：我们假设它是一个矢量。这样，如果力是一个矢量，那么，由于我们知道加速度是一个矢量，因此，方程（1.13）在任意坐标系下看起来都将一模一样。以一种不显含x,y和z的形式写下牛顿定律具有这样的好处，从今以后，每当我们要写下牛顿方程或者其他物理定律时，再也不需要写出三条定律了。表面上看，我们写下一条定律，但实际上对每一个特定的坐标系，自然就是三条定律，原因就是，任何矢量方程表示，方程两边各个分量相等。

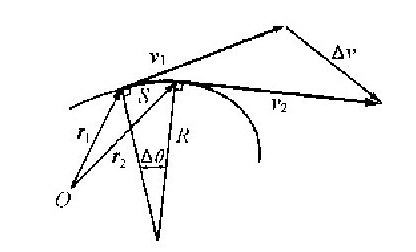
图1-7　一条弯曲的轨道

加速度是速度矢量的变化率，这个事实有助于我们在某些相当复杂的情况下计算加速度。比如说，假设一个粒子正在一条复杂的曲线上运动（图1-7），而且在某个特定的时刻i具有确定的速度ν1，而当到达另一个稍晚一点的时刻i2时，它具有不同的速度ν2。加速度是什么呢？答案是：加速度就是速度之差被这个小的时间间隔除，这样，我们就需要用到两个速度之差。我们如何得到速度之差呢？为了把两个矢量相减，我们过ν2和ν1的终点画出这个矢量；即，取△作为两个矢量之差，对吗？不对！只有当矢量的尾部放在同一点上时，上面的做法才行得通！如果我们把矢量移到别的某处再画一条直线过来，就毫无意义了，因此，务必要注意这一点！为了把矢量相减，我们必须画一个新的示意图。在图1-8中，ν1和ν2均被画成与图1-7中它们的对应部分平行而且相等，这样我们就能够讨论加速度了。加速度当然就是△ν/△i。有趣的是能够将速度之差分解成两个部分；我们可以把加速度看成具有两个分量，一个是与路径相切方向上的△ν‖，另一个是与路径成直角的△v⊥，如图1-8所示。与路径相切的加速度当然只是矢量长度的改变，即速率v的改变：

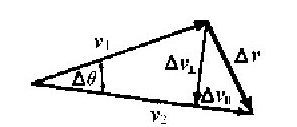
图1-8　计算加速度的示意图

利用图1-7和1-8计算加速度的另一个与曲线正交的分量是很容易的。在短时间△i内，设ν1和ν2之间的角度改变是一个小角△θ。如果速度的大小用v标记，那么，自然就有

△v⊥=v△θ

而加速度a就是

a⊥=v（△θ/△i）

现在我们需要知道△θ/△i的值，它可以按照以下方法求出：在某个确定的时刻，如果曲线近似于某个具有确定半径R的圆，那么，在时间△i内距离S自然就是v△i，其中v是速率。

△θ=v（△i/R），或者△θ/△i=v/R.

因此得到

与先前见过的一样。