上述的观察引导爱因斯坦提出这样一个建议,如果我们设想,一个物体的质量等于它的总能量被c2除,那么,物体的质量就能够表示得比公式(3.1)更简单。如果用c2乘公式(3.11),结果就是

在公式中,左边的项表示一个物体的总能量,右边最后一项就是普通的动能。爱因斯坦把那个很大的常数项m0c2解释成是该物体的总能量的一部分,它是一种叫做“静能”的固有能量。
让我们跟随爱因斯坦探究一下,物体的能量总是等于mc2这个假设有些什么推论。作为一个有趣的结果,我们将导出质量随速度变化的公式(3.1),到目前为止,我们只是把这个公式当做假设来看待。我们从处于静止状态的物体开始,这时,它的能量是m0c2。接着,我们对这个物体施加一个力,这个力使物体开始运动并给予它动能;因此,由于能量增加了,质量也就增加了——这已经隐含在最初的假设中了。只要力继续作用,能量和质量两者就会不断地增加。我们已经看到(第13章9),能量对时间的变化率等于力乘以速度,也就是

我们还有(第9章10公式9.1)F=d(mv)/dt。当这些关系与能量的定义结合起来时,公式(3.13)就变成

我们希望求解这个方程得到m。为了这样做,我们首先利用一个数学技巧,在方程的两边乘2m,把方程变成
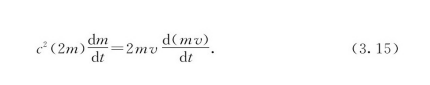
我们需要把导数除去,这可以通过对方程的两边做积分来实现。可以看到(2m)dm/di这个量是m2的时间导数,而(2mv)·d(mv)/di则是(mv)2的时间导数。因此,方程(3.15)等同于

如果两个量的导数相等,这两个量本身最多相差一个常数,比如说C。这使我们能够写下

我们需要更明确地确定常数C。由于方程(3.17)必定对所有的速度都成立,因此我们可以选择v=0这个特别的情形,并且认为这种情况下的质量就是m0。把这些量代入方程(3.17)中就得出
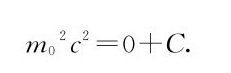
现在可以把这个C值代入方程(3.17)中,方程变成

用c2除并重新整理各项就得出
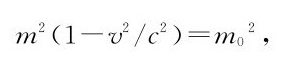
由这个结果我们得到

这就是公式(3.1),正好就是为了使公式(3.12)中的质量与能量相一致所需要的。
通常,这些能量变化相当于质量上非常轻微的改变,原因就是,我们平时不可能从一定量的材料中产生许多能量;但是,以一个爆炸能量相当于2万吨级TNT的原子弹为例,可以证明,由于能量被释放出来,爆炸之后的残余物比反应材料的初始质量轻了1克,也就是说,根据关系式△E=△mc2,被释放出来的能量具有1克的质量。利用物质湮没而完全转变成能量的实验,这个关于质量与能量的等效性的理论已经被完美地证实:一个电子和一个正电子在静止状态下被放在一起,每一个带有静质量m0。当它们碰到一起时,就会蜕变成两束伽马射线,每一束射线具有精确的能量m0c2。这个实验提供了一个直接的方法,用来确定与一个粒子的静质量相联系的能量。

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
















