小球碰撞的动量和动能

我们在上一章中认识到，物体的质量随着速度的增加而增加，但是，我们并没有像论证时钟的行为那样对此做过论证，从这个意义上说，我们并没有给出上述结论的任何说明。然而，我们能够证明，作为相对性原理和其他几个合理的假定的结果，质量必定按照这样的方式改变。（假如我们希望做有意义的推论，就不得不说“其他几个假定”这句话，因为，除非我们拥有某些假定为正确的定律，否则我们不可能证明任何结论。）为了避免研究力的变换定律，我们将分析一个碰撞问题，在这个问题中，除了假定动量和能量守恒之外，我们不需要知道关于力的任何定律。我们还要假定，运动粒子的动量是一个矢量，并且总是指向速度的方向。不过，我们将不再像牛顿那样，假定动量是一个常数乘以速度，而只是假定它是速度的某个函数。因此，我们把动量矢量写成某个系数乘以速度矢量：

我们在系数中写上一个下标v以提醒自己，这是一个速度的函数，并一致把这个系数mv叫做“质量”。当然，如果速度很小，它与那个通常在慢速运动的实验中测量到的质量是一样的。下面，我们将尝试从相对性原理，即物理定律在各个坐标系中必定相同，来论证mv的表达式必定是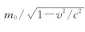假定有两个粒子，比如两个质子什么的，它们完全相同，并且以完全相等的速度彼此朝向对方运动。他们的总动量等于零。那么会发生什么事情呢？碰撞之后，它们的运动方向必定正好彼此相反，因为如果它们不是正好相反的话，就会存在一个非零的总动量矢量，而动量就不再守恒。它们还必定具有相等的速率，因为它们是完全一样的实体；事实上，它们必定具有与开始运动时同样的速率，因为我们假定在这些碰撞中能量是守恒的。所以，一个弹性碰撞，即可逆的碰撞，其示意图就会如图4-2（a）所示那样：所有的矢量长度相同，所有的速率相等。我们将假定，这样的碰撞总是能够安排下来的，任何角度θ都有可能发生，并且，在这样一种碰撞中，任何速率都可以用到。接下来我们注意到，同样这个碰撞可以通过坐标系的转动从不同的角度去观察，而正是为了方便起见，我们将把坐标系转到这样一个方位，使它的横轴将两个运动平均分开，如图4-2（b）所示。这是重新画出来的同一个碰撞的示意图，只不过把坐标轴转了个方向而已。

真正的技巧在于：让我们从某个观测者的角度来看看这个碰撞，这个观测者乘坐在一辆往前行驶的汽车中，这辆汽车的速度等于某个粒子的速度的水平分量。结果，这个碰撞看起来怎样呢？它看起来就好像第一个粒子正好笔直地向上运动，因为它的速度已经没有水平分量了，接着它又笔直地向下运动，也是因为它的速度没有水平分量。这就是说，这个碰撞看起来就如图4-3（a）所示那样。然而，第二个粒子却正以另一种方式运动，当我们乘车而过时，它看起来就好像以某个惊人的速度成一个较小的角度飞逝而过，但是，我们能够意识到，碰撞前和碰撞后的角度是相等的。让我们用u标记第二个粒子的速度的水平分量，用w标记第一个粒子的垂直速度。

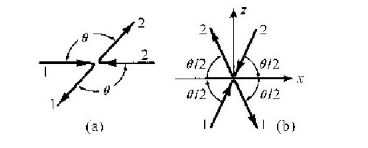
图4-2　两个相同的物体之间弹性碰撞的两种视图，这两个物体正以相同的速率朝相反的方向运动

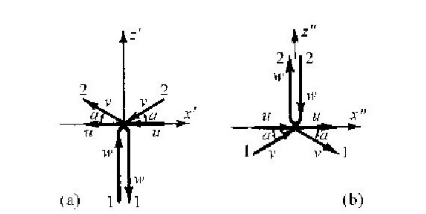
图4-3　从运动的汽车上去看碰撞的另外两种视图

下面的问题是，垂直速度utanα等于什么？如果我们知道这个量的话，就可以利用垂直方向上动量守恒的规律得到动量的正确的表达式。显然，动量的水平分量是守恒的：两个粒子在碰撞之前和碰撞之后的动量是相等的，而对第一个粒子来说这个量等于零。因此，我们只需要将守恒定律用到向上的速度utanα。但是，我们可以通过用另一种方式观察这同一个碰撞来得到向上的速度！如果我们从一辆（相对于第一个粒子）以速率u向左运动的汽车上观察图4-3（a）所示的碰撞，那么，我们看到同一个碰撞，只是如图4-3（b）所示的那样“颠倒”了。现在，第二个粒子是那个以速率w上下运动的粒子，而第一个粒子有了水平的速率u。当然，我们现在知道速度utanα等于什么了，它就是：

[参见公式（4.7）]。我们知道，做垂直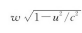运动的粒子的垂直动量的改变是

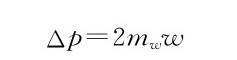
（因子2是因它上下运动引起的）。那个斜向运动的粒子具有某个速度v，我们已经知道它的分量是u和w，而它的质量则是mv。因此，这个粒子的垂直动量的改变就是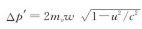，因为，根据我们假定的规则（4.8），动量的分量总是等于与速度的数值相对应的质量乘速度在所考虑的那个方向的分量。这样，为了使总动量等于零，垂直方向的动量必定相抵消，于是，以速率w运动的质量和以速率v运动的质量之比必定等于

我们来考虑w是无穷小的极限情形。如果w的确非常小，那么显然v和u实际上是相等的。在这种情况下，mw→m0，还有mv→mu。于是得到一个重要的结果

下面做一个有趣的练习，假定公式（4.10）是质量的正确表达式，检查一下公式（4.9）在任意的w值时是否确实成立。注意在公式（4.9）中要用到的速度v可以通过直角三角形来计算：

虽然我们刚才只是在小w的极限时使用这个公式，但我们将发现它是不言自明的。

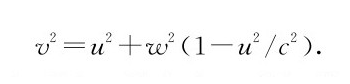
那么，让我们接受动量守恒和质量按照（4.10）式依赖于速度这两个结论，并继续考察我们还能得到别的什么结论。我们来考虑一种通常叫做非弹性碰撞的现象。为了简单起见，假定有两个以相等速率w朝相反方向运动的同类物体，它们如图4-4（a）所示那样相互碰撞后黏在一起，变成某个新的静止的物体。每一个物体相应于w的质量m，正如我们所知，等于如果假定动量守恒和相对性原理成立，那么，就能够说明一个有趣的、与这个新形成的物体的质量有关的事实。设想一个与w成直角的无穷小的速度u（我们可以用有限的u值做同样的处理，不过，用一个无穷小的速度更容易理解），然后，在一部速度等于-u的电梯上考察这同一个碰撞。我们所看到的现象如图4-4（b）所示。复合物体具有一个未知的质量M。现在，第一个物体以一个向上的速度分量u和一个实际上等于w的水平速度分量运动，第二个物体也一样运动。碰撞之后，就得到以速度u向上运动的质量M，假定这个速度u与光速相比是非常小的，与w相比也是很小的。动量必须守恒，因此，我们来估计一下碰撞之前和碰撞之后沿着向上方向的动量。在碰撞之前，我们有p≈2mwu，而在碰撞之后，动量显然是p'=Muu，不过，因为u是如此之小，所以Mu基本上与M0一样。由于动量守恒，所以，这些动量必定相等，因此便有

图4-4　质量相同的物体之间的非弹性碰撞的两种视图

由两个相同的物体碰撞而形成的物体，其质量必定是相互碰在一起的物体的质量的两倍。大家也许会说，“是的，当然是这样的，这就是质量守恒嘛。”可是，这并不是那么容易就“当然是这样的”，因为，与它们静止不动时应该具有的质量相比，这些质量已经增大了，尽管如此，它们仍然有贡献，但是，对总的M来说，它们所贡献的并不是处于静止时具有的质量，而是更多。这看起来也许非常令人惊讶，为了使两个物体相互碰撞时动量守恒有效，即使这两个物体在碰撞后停了下来，它们结合后的质量也必定大于这两个物体的静质量！