6-1 二维弯曲空间
牛顿认为,每个物体都吸引别的物体,吸引力的大小与两者之间的距离的平方成反比,而物体则以正比于力的加速度回应力的作用。以上说法就是牛顿的万有引力定律和运动定律。正如大家所知道的,这些定律解释了球体、行星、人造卫星、星系等物体的运动。
爱因斯坦对万有引力有一种不同的解释。他认为,重物附近的空间与时间(它们必须被组合起来形成空时)是弯曲的。物体在这个弯曲的空时中极力要沿着“直线”运动,这种趋势令它们以这样的方式运动。这是一个很难理解的概念——非常难以理解。这就是我们在本章中要做出解释的概念。
我们这个主题有三部分内容。一部分涉及引力效应;另一部分涉及已经讨论过的空时概念;第三部分涉及弯曲空时的概念。在开始时我们将简化要讨论的主题,不去过多地考虑引力的问题,并且不考虑时间变量——仅仅讨论弯曲的空间。稍后我们将讨论另外两个主题,但目前将集中讨论弯曲空间的观念——弯曲空间是什么意思,或者更准确地说,在爱因斯坦的理论中,弯曲空间是什么意思。结果表明,在三维空间中,甚至这样的问题目前也是有点难以理解的。因此,我们将首先更进一步简化这个问题,在二维的情况下讨论“弯曲空间”这个词的含义。
为了理解二维弯曲空间这个概念,你确实必须去体会一下一个生活在这种空间中的生物那带有局限性的观点。假如我们想象一只生活在一个平面上的没有眼睛的虫子,如图6-1所示。它只能在这个平面上运动,它没有认识“外部世界”的方法。(它并没有大家所具有的想像力。)我们当然要通过类比的方法来讨论。我们生活在一个三维的世界中,我们没有任何想像力去想象一个新的方向跳离我们这个三维世界;因此,我们不得不通过类比的方法来解决问题。这就好像我们是生活在一个平面上的虫子,在另一个方向存在着一个空间。这就是我们将首先通过虫子进行讨论的原因,记住,它必须生活在它的表面上,并且不能跳出去。
图6-1 一只在平面上的虫子
再举一个例子来说明一只生活在二维中的虫子,我们来想象一只生活在一个球面上的虫子。想象它能够如图6-2所示那样在球面上到处漫游,但它不能朝“上”,或者朝“下”,或者朝“外”看。
下面我们还要看一看第三种生物。它像别的两种生物一样也是一只虫子,也像我们的第一只虫子那样生活在一个平面上,但这个平面是特殊的。温度在不同的地方并不一样。还有,这只虫子以及它所使用的任何尺子都由遇热膨胀的相同的材料构成。每当它在某个地方放上一把尺子来测量某个东西时,这把尺子就立刻膨胀到该处温度下的固有长度。无论它把什么东西放在哪里——它自己、一把尺子、一个三角形,或者什么别的东西——这件东西自然就会因热膨胀而伸长。所有的东西在热的地方都比在冷的地方长,所有的东西都具有相同的膨胀系数。我们特别要考虑一种特殊的热板,它在中心处是冷的,随着我们往边上走,它变得越来越热(图6-3),尽管如此,我们还是要把我们这第三种虫子的家园叫做“热板”。
图6-2 一只在球面上的虫子
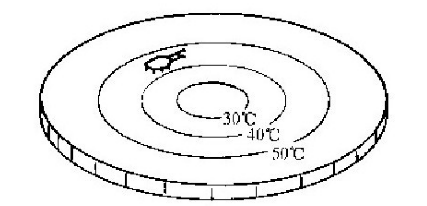
图6-3 一只在热板上的虫子
下面我们将想象这些虫子开始研究几何学。尽管我们把它们想象成是瞎子,这样它们就看不到任何“外部的”世界,但是,它们还是能够用它们的腿和触角干许多事情。它们能够画线、做尺子、测量长度。首先,设想它们从几何学中最简单的概念开始。它们学会怎样画一条直线——定义为两点之间最短的线。我们的第一种虫子(图6-4)会画非常直的线。可是生活在球面上的虫子怎样呢?它沿着两点之间——对它而言——的最短距离画出它的直线,如图6-5所示。这条线在我们看来也许像一条曲线,可是它没有任何办法跳离球面并发现“真的”有一条更短的线。它只知道,假如它在它的世界中尝试任何别的路线,它们都比它的直线长。因此,我们将让它把它的直线作为两点之间最短的弧线。(这当然是一个大圆上的一条弧线。)
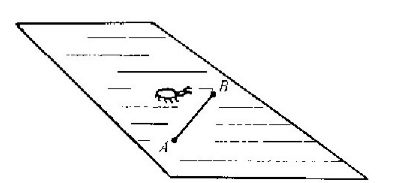
图6-4 在一个平面上画一条“直线”
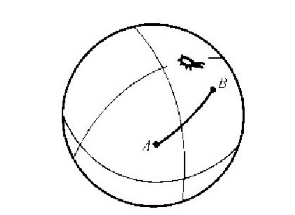
图6-5 在一个球面上画一条“直线”
最后,我们的第三种虫子(图6-3中的那种)也将画出一条在我们看来像曲线的“直线”。比如说,在图6-6中A和B之间的最短距离应该在一条如图所示的曲线上。为什么会这样呢?原因就是,当它的线朝外向着热板的较温暖的部分弯曲时,尺子(从我们那无所不知的观点来看)就逐渐地变得更长,而从A到B需要首尾相接地放置的“码尺”就更少。因此,对它来说,这条线是笔直的——它没有任何办法知道,在外部的一个陌生的三维世界中会存在某种生物,这种生物将把一条不同的线叫做“笔直的”。
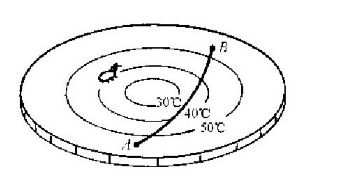
图6-6 在热板上画一条“直线”
我想,大家现在得到了这样一个概念,因此,余下的全部分析都将总是从生活在特定的表面上的生物的观点出发而不是从我们的观点出发。记住这个要求,我们来看一看它们的几何学的余下部分是个什么样子。让我们假定这些虫子全都学会了怎样画两条相交成直角的线。(你能够想象出它们会怎样做这件事。)于是,我们的第一种虫子(生活在普通平面上的那种)发现了一个有趣的事实。如果它从A点开始画一条100英寸(1英寸约为2.540厘米)长的线,然后转过一个直角并画另一条100英寸的直线,然后再转过一个直角并再画一条100英寸的直线,然后第三次转过一个直角并画第四条100英寸长的直线,它就会如图6-7(a)所示的那样,最后刚好画到开始的那一点上。这是它的世界的一个性质——它的“几何学”中的一个事实。
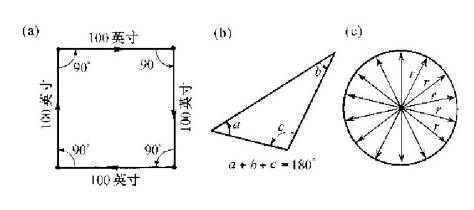
图6-7 在一个平直的空间中的正方形、三角形和圆
接着,它发现另一件有趣的事情。如果它画出一个三角形(一个由三条直线组成的图形),那么,三个角度之和就等于180°,即等于两个直角之和。参见图6-7(b)。
接下来,它画了一个圆。一个圆是什么东西呢?一个圆是这样画出来的:你从某个点出发向四面八方画直线,并标上许多与这个点距离相同的点。参见图6-7(c)。(我们必须小心在意我们是如何定义这些东西的,因为我们必须让另外两个家伙能够做类比。)当然,这个图形等价于这样一条曲线,你可以通过让一把尺子绕着一个点旋转来画出它。不管怎么样,我们这些虫子学会了怎样画圆。接着有一天,它想测量一个圆的周长。它测量了几个圆,并发现了一条简洁的关系:圆周的长度总是等于同一个数字乘半径T(这当然就是从中心向外到曲线的距离)。周长与半径总是具有相同的比例——近似等于6.283——与圆的大小无关。
下面,我们来看一看别的两种虫子在它们的几何学中找到些什么东西。首先,当生活在球面上的虫子尝试画一个“正方形”时会出现什么事情呢?如果它遵循我们在前面描述的方法去做,它大概会认为结果几乎不会有什么麻烦。它得到了一个如图6-8所示那样的图形。它的终点B并不在起点A上,根本就画不出一个闭合的图形。拿一个球来试一试看。类似的情况出现在我们那生活在热板上的朋友那里。如果它画四条由直角连接起来的(用它的膨胀的尺子测量时)长度相等的直线,它就得到一个像图6-9那样的图形。
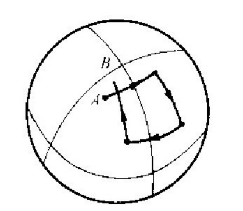
图6-8 尝试在一个球面上画“正方形”
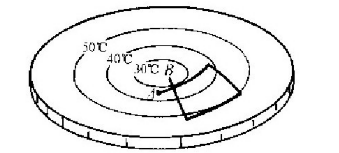
图6-9 尝试在热板上画“正方形”
下面假设我们的每一种虫子都有它们自己的欧几里得,它已经告诉它们,几何学“应该”是个什么样子,而它们已经在一个小的范围内通过进行粗略的测量大致上验证了它的结论。接着,当它们尝试在一个大的范围内画精确的正方形时,就会发现出错了。问题就在于,仅仅通过几何学的测量,它们就会发现,麻烦出在它们的空间中。我们定义弯曲的空间是这样一个空间,在这个空间中,几何学并不是我们在平面上预期的那个样子。生活在球面上或者生活在热板上的虫子的几何学是弯曲空间中的几何学。欧几里得几何学的法则失效了。于是,为了认识到你生活于其中的世界是弯曲的,并不需要你能够使自己从表面上跳出来。为了认识到世界是一个球面,并不需要做环球航行。通过画一个正方形,你就能够认识到,你生活在一个球面上。如果画出来的正方形很小,你将需要很高的精确度,不过,如果这个正方形很大,测量就能够比较粗略地进行。
让我们以平面上的三角形为例子。3个内角之和等于180°。我们在球面上的朋友能够找到非常奇特的三角形。例如,它能够找到具有3个直角的三角形。千真万确!图6-10画出了一个。想象我们的虫子从北极开始画一条直线,一直往下画到赤道上。接着,它转过一个直角,并画出另一条长度一样的精确的直线。接着重复上面的步骤。用这个它挑选出来的非常特别的长度,正好回到开始的那一点,而且也是以一个直角与第一条线相交。因此,毫无疑问,对于它来说,这个三角形有3个直角,或者说内角之和是270°。结果,三角形的内角之和总是大于180°。事实上,多出的度数(对于图示的那种特殊的情形,就是多出的90°)与该三角形的面积成正比。如果一个在球面上的三角形非常小,它的内角之和就非常接近180°,仅仅大一点点。随着三角形不断增大,偏差就不断增加。生活在热板上的虫子从三角形中会发现相似的困难。
下面来看一看我们那些虫子在圆这个问题上找到些什么东西。它们画出圆周并测量其周长。比如说,生活在球面上的虫子可以画一个如图6-11所示那样的圆。它将发现圆的周长小于2π乘半径。(你能够明白这个结果,因为根据我们的三维视图的常识,它所谓的“半径”显然是一条比这个圆的真实半径更长的曲线。)设想生活在球面上的虫子学过欧几里得几何学,并决定用周长除2π来预言半径:
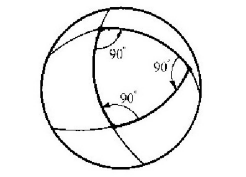
图6-10 在球面上一个“三角形”可以有3个90°的内角
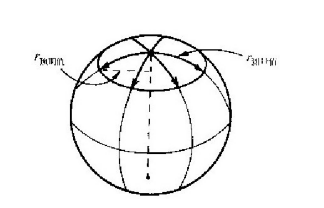
图6-11 在球面上画一个圆

于是,它就会发现,实测半径大于预期半径。继续研究这个问题,它可以把这个差额定义为“多出的半径”,写成

并研究这种多出半径的效应怎样依赖于圆的大小。
我们那生活在热板上的虫子将发现相似的现象。想象它准备画一个如图6-12所示那样的圆,圆心在板上冷的部位。假如我们打算看着它画这个圆,就会注意到,它的尺子在靠近圆心处是短的,并随着尺子往外移动逐渐变长——尽管这只虫子无疑并不知道这一点。当它测量周长时,尺子自始至终是长的,因此,它也发现实测半径比预期半径C/2π长。热板虫也发现一种“多出半径的效应”。这种效应的大小还是依赖于圆的半径。
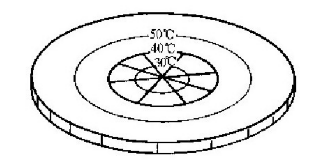
图6-12 在热板上画一个圆
我们将把这样一个空间定义为一个“弯曲空间”:在这个空间中,存在以下类型的几何误差:一个三角形的内角之和不是180°;一个圆的周长被2π除不等于半径;画一个正方形的规则并不给出一个闭合的图形。你还可以想出其他的事情。
我们已经举出了弯曲空间的两个不同的例子:球面和热板。不过,如果我们选择热板上的温度变量是距离的适当的函数,那就有意思了,两种几何学将会一模一样。这个结果相当有趣。我们能够令生活在热板上的虫子与生活在球面上的虫子得到完全相同的答案。对于那些喜欢几何学及几何学问题的人,我将告诉你们这如何能够办得到。如果你假定尺子的长度(当由温度决定时)正比于1加上某个常数乘以与原点的距离的平方,那么,你就会发现,那块热板上的几何学在所有细节上(无穷远点除外)与球面上的几何学一模一样。
当然,存在别的种类的几何学。我们可能会向一只生活在一个梨形面上的虫子请教几何学,所谓的梨形面就是这样一种曲面,在某些地方具有较大的弯曲程度,而在别的地方具有较小的弯曲程度,这样,在它的世界中,在某个区域画出的小三角形与在另一个区域画出的相比,内角的超出就会更加严重。换句话说,空间的弯曲程度有可能处处不一样。这正是上述观念的一个推广。它也可以用热板上一个适当的温度分布来模拟。
我们还可以指出,有可能出现负的偏差这种结果。比如说,我们会发现,所有被画得非常大的三角形都具有小于180°的内角和。这看上去也许不可能,但情况确实如此。首先,我们可以做一个温度随着远离板心而降低的热板,于是,所有的效应都将反过来。不过,我们也可以考察鞍形面的二维几何学,用单纯的几何方法实现这种结果。想象一个如图6-13所示的鞍形面。接下来在这个面上画一个“圆”,它被定义为中心距相同的所有的点的轨迹。这个圆是一条具有起伏效应的振荡的曲线。这样,它的周长就比用2πT算出的预期值要长。因此,在这里C/2π就比T大。“多出的半径”是负的。
球面和梨形面等曲面都是正曲率的表面;而其他的面叫做负曲率的表面。一般说来,一个二维的世界将具有处处不一样的曲率,并且有可能在某些地方曲率为正,而在别的地方曲率为负。概括地说,弯曲空间指的就是这样一种空间,在这些空间中,由于出现正的或负的偏差而使欧几里得几何学失效。曲率的大小(比如说由多出的半径来定义)可以处处不一样。
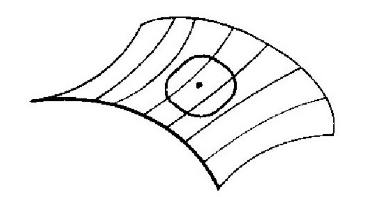
图6-13 鞍形面上的一个“圆”
应该指出的是,从我们对曲率的定义来看,一个圆柱面不是弯曲的,这相当令人惊讶。如果一只虫子生活在一个如图6-14所示那样的圆柱面上,它就会发现三角形、正方形和圆全都具有平面上相应图形所具有的性质。只要考虑一下,假如圆柱面被展开成平面,所有这些图形看起来会怎样,就很容易明白这一点。于是,可以用完全与平面相对应的方法画出所有的几何图形。因此,一只生活在一个圆柱面上的虫子(假定它不会一直走下去,而只是做局部的测量)没有任何办法察觉它的空间是弯曲的。在我们的理论直觉中,我们认为它的空间不是弯曲的。我们要谈论的东西更确切地叫做内部曲率:即只在局部区域进行测量就能够得出的曲率(一个圆柱面没有内部曲率)。爱因斯坦说我们的空间是弯曲的,他所指的就是这个意思。不过,到目前为止,我们仍然只是在二维的情况下定义了弯曲空间的概念;我们必须接着看一看,这个概念在三维的情况下可能会有什么意义。
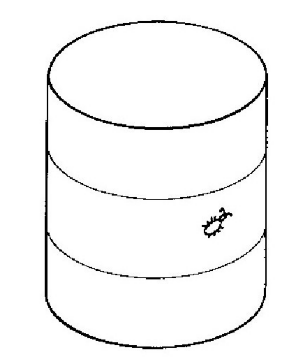
图6-14 一个内部曲率等于零的二维空间
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。


















