地下的暗流

大英图书馆说明

这一页没有插图，列奥纳多·达·芬奇在这一页描述了在淡水和咸水同时出现的地方的地球暗流，并推测这些水如何在大海底部交汇。

“很多咸水暗流在距离大海特别远的地方出现，这可能是因为暗流穿过某些盐矿……像一个巨大的采石场，大块大块的盐被开采出来。在很多被盐水围绕的石头中或盐块中发现有充满淡水的暗流。……海水从散乱分布在海底的盐矿中提取淡水，淡水必然会融入海水内。在大海的底部确实有淡水存在。对这一点我个人比较确定。地球内部散散乱乱、相互交织的暗流均在大海底部交汇。”

他联想到观察地下泉水的现象，强调曾经参观过的一个地方。“有些地方的暗流会出现6个小时，然后再消失6个小时。我在科莫湖亲眼看到过一条名为普林尼泉的暗流，泉水时隐时现，以至于流过的地方，养育着好几个磨坊。潜流流下的时候，落差特别大，流水好像掉入深井中一般。”

列奥纳多·达·芬奇同时讨论了表面水流对海底和海岸的影响之间的关系。这个讨论点似乎要描述水体的联结方式影响水流运动。

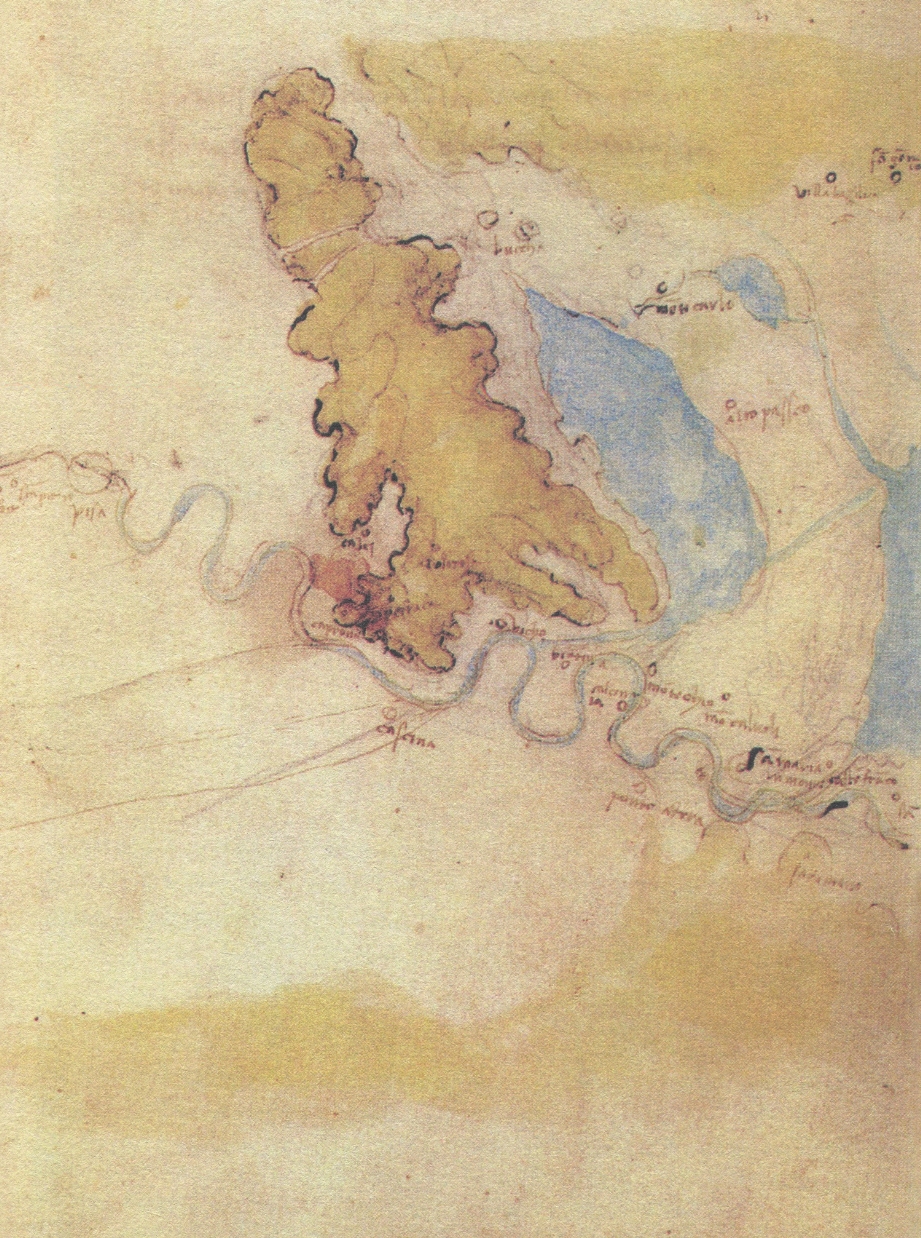
在这七页中，有关于水及水底的657项观察

二十一项案例

处在宇宙中心的重力特征，可以通过地面实验在一定程度上得以证实。力实验有关的物体要水平放置，不能高也不能低，因为实验面无法涵盖太大不过在水平半球上操作，效果会更佳。宇宙中心大部分自然物被中心线均分中心线上，悬挂的重物重量会尽可能地靠向宇宙中心。而且，不但如此，这会穿过悬挂物的临时中心，这可以通过横向悬挂的锥体看到，图4和图5并列。

从泄洪闸流入大海的水流，沿着笔直的水道，流速要比源头的水流快泄洪闸打开后，从泄洪闸水道口流出的水流，和冲向泄洪闸口的水流速度流出水的水道和接受水流的水道，材质相同且尺寸相等。而假如流入的水道出的水道窄，根据两个水道的宽度比例，稍窄的水道比较宽的水道流速要快很多。

而假如流水进入的水道，比流水流出的水道截面较大，那么前后水流速同两条水道之间的部分尺寸比例相同，但流速正好相反。从湖泊流下来布，穿过空气，如果瀑布比较长，则水会在固定的时间内下降到底，因为分水重量增加，吸引了其他部分的水。就如大家所认为的，水的表面有自身存在的韧性，这可以通过观察气泡看到。那么，你肯定会赞同，水的数量越大，这种韧性就越强。

水流在下降的过程中越慢，在规定的时间内下降的水的数量就越小。一定数量的水，在穿过空气降落的过程中所使用的时间越长，在一定的时间内水流的速度越慢——这是在与同样重量的水在同样条件下一次性穿越空气、倾盆而下进行对比。这种现象的发生是因为，在整体流水中，假如水流的一股像一条线，为一个米粒的重量，那么1 000条线就有1 000个米粒的重量，这些水流如果单独称重，在空气中的重量几乎微乎其微，其运动因此也极慢；但如果将1 000个米粒合成一个重量，让其穿过空气降落，这些重力运动会比单一米粒运动的速度快1 000倍。

海上的风暴在海边比大海上要凶猛很多。这是因为海浪的回弹力从一个方向冲击大海，而风在相反的方向冲击，从而使浪变得更高、更薄。当风从西方吹来，水从河口流出后朝南流动；当风从西南方向吹来，水流朝南流动；或者是，风从东南方向吹来，水流朝东流动。

然后，用几个容器和水管连接在一起来做实验，将一个容器的水通过同样厚度的水管抽到另一个容器内。在一定时间内，水管放进水中的深度越深，水管抽取的水越多，即使是水管的管径相同，水的降落高度也相同。

水的反射运动比入射运动要慢很多，因为水中的反射冲击力在海水中几乎没有运动，反射速度到达海水后，无法将海水推走，因此只是对第一次的反射形成新的反射阻碍。入射运动在出发点或半路一般没有形成浪；而反射运动则在出发点或半路掀起很高的浪。

在不太宽阔的峡谷中，河流的流速总是会变来变去。假如我们将峡谷的出口堵截，让河流蓄水一两个冬季，峡谷中的泥沙会慢慢沉积。然后在需要导出河流的地方开挖出口，那么河水会从所挖的出口方向流出。

将一定数量的水从一个量杯倒入同样型号的另一个量杯，第二个量杯水量和水位同第一量杯相同，或者水位高低稍微有所出入。落入深水池塘的水，水流总是会冲击池塘的底部，或者受到池塘底部的冲击。表面的水落入底部会出现很多情况，对底部冲击力的大小也有所不同。在较深的池塘中，水层中部的水如何到达水面？水层中部的水又如何到达池塘的底部？底部的水如何到达中部？水面的水如何降低到水层中部？

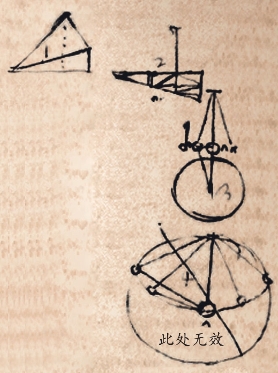
假设重力点A为宇宙中心

如果想确切知道重物各部分圆周直径上的重力，通过上述这种方式，可以科学分割，而不用将物体切开；可以按照下列图示操作，通过这个方法，可以获得想要知道的任何不规则物体任何部分的重量，而且屡试不爽。

ro之间为任何一个物体的直径，或者是你所想知道的第二、第三、第四个物体重量的直径。当然，首先要知道物体的重量。假设这个圆环为3磅，而我想从里面减去1磅。将这个重物悬挂在垂直线nm的旁边，这样大家知道重物的中心在上述的垂直线上，然后在旁边放一个1磅的物体，这个物体将3磅的物体推离垂直线，而将2磅保留在垂直线的左边，2磅在垂直线的右边。现在切去3磅物体超过垂直线的部分，那么就剩下1磅，记住：垂直线nm的两侧均为2磅。

垂直线两侧均为2磅。