弦理论的唯一性问题可以通过对偶性方法得到解决。对偶性最开始是作为假设而被引入弦理论的,实际上到现在这些假设也没有得到严格的证明。但是由于已经通过各种各样的非平凡检验,在该领域工作的大多数人都相信弦理论中的对偶性的确是存在的。所谓的对偶性是说两个或多个明显不同的弦理论实际上是等价的(图5.12)。对偶关系有以下两个最重要的特点。
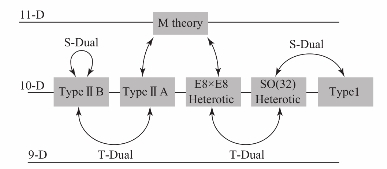
图5.12 不同弦理论之间的对偶性
(1)通过对偶映射一个弦理论中的基本粒子在另一个弦理论中表现为复合粒子。基本粒子与复合粒子的分类变得毫无意义,因为这依赖于选择哪个特殊的理论来描述该系统。
(2)对偶性通常把一个强耦合理论与一个弱合理论联系在一起。如果g与ɡ分别表示两个理论的耦合常数,对偶变换使得它们之间满足简单关系g=ɡ-1。因此按耦合常数ɡ进行的微扰展开在对偶理论中包含g的非微扰效应。特别是一个理论中的树图(经典)结果给出对偶理论中的微扰求和与非微扰效应。很明显对偶性是弦量子论而不是其经典极限的性质。为人们所熟悉的对偶有6种,分别是:①第二型A弦理论与第二型B弦理论之间的对偶;②E 8×E 8与SO(32)杂化弦之间的对偶;③SO(32)杂化弦与9+1维第一型弦理论之间的对偶;④紧致在4维环面T 4上的E 8×E 8与SO(32)杂化弦与K3曲面上的第二类B型超弦理论之间的对偶;⑤紧致在6维环面T 6上的E 8×E 8与SO(32)杂化弦的自对偶,即耦合常数为g的理论等价于耦合常数为g-1的理论;⑥第二型B超弦理论是自对偶理论。
上面提到的几种对偶性可以分为两类:T-对偶指紧致在半径为R的圆上的一种理论与另一个紧致在半径为1/R的圆上的理论之间的等价。所以T-对偶联系的两个理论一个紧致在很小的圆上而另一个紧致在一个很大的圆上(甚至完全不紧致),但却描述相同的物理;S-对偶讨论一种理论的强耦合极限与另一种理论的弱耦合极限之间的等价性。通过各种紧致化下不同弦理论之间的对偶性,我们可以得到弦理论的一个大统一图像。存在一个现在被称为M理论的10+1维单一理论,M理论在不同的极限下表现为不同的弦理论。例如,我们把11维的M理论紧致到一个小圆上(图5.13),可以得到第二型A超弦理论;把11维的M理论紧致到一个很短的线段上(图5.14),则得到E 8×E 8的杂化弦理论。M理论的低能极限是10+1维超引力理论。有关M理论的研究工作还处于初级阶段,至今甚至M理论的定义也还不明确。但一般认为,起码在无穷动量系M理论可以由矩阵理论来描述。M理论的出现一度使某些理论物理学家乐观地认为我们现在正处于一个与20世纪初量子论发展初期非常相似的阶段。
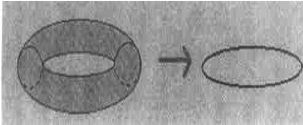
图5.13 紧致在小圆上的11维M理论等价于10维弦理论
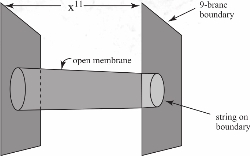
图5.14 紧致在短线上的11维M理论等价于10维弦理论
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
















