平衡压强的计算公式

压强的平衡条件为

其中， 燃气生成率和质量流率由式 （8-2） 给出。 显然， 采用不同的燃速定律， 可以得到不同的计算公式。

以指数燃速定律式 （3-7） 为例， 并考虑侵蚀燃烧效应， 有

式中， φ（ ） 为平均侵蚀函数， 其定义见式 （3-37）。 将上式代入平衡条件式 （8-14），可得

因为此时的压强p为平衡压强peq，所以上式可整理成

令

称为面喉比， 并将特征速度的表达式 （6-102） 代入式 （8-15）， 则有

定义装填参量M和密度比δ为

装填参量M的单位为Pa1-n或MPa1-n。于是，可将平衡压强改写为

显然，δ＝δ（peq），所以式（8-15）、式（8-17） 或式（8-20） 均为隐式方程，需要迭代求解。

由于ρ≪ρp，即δ≪1，为了简化计算，将式（8-20） 中的指数项展成幂级数，并忽略高阶项， 可得

于是， 式 （8-20） 变为

再将密度比定义式 （8-19） 代入上式， 整理可得

或者， 不计δ的影响， 即令δ＝0， 有

通常， 忽略δ带来的计算误差约在2％以内。

上述各式均为计算平衡压强的常用计算式， 其中， 式 （8-21） 和式 （8-22） 为显式公式， 可直接计算出平衡压强， 其余公式则为隐式公式， 需要迭代计算。

采用隐式方程迭代计算平衡压强peq时，计算步骤为：

（1） 令δ＝0，即采用式（8-22） 计算，得到peq的初值。

（2） 以peq的初值代入式（8-19） 求解δ。

（3） 用式（8-20） 求解出新的peq。

（4） 返回第（2） 步，用peq的新值再求解δ，于是又得到peq的新值。如此重复迭代，直到相邻两次的peq值相差小于所要求的精度εp为止，如图8-2所示。

图8－2 平衡压强迭代计算过程

通常情况下，由于用显式方程（8-22） 求出的peq误差并不大，所以上述过程的迭代次数不会很多， 一般数次迭代即可满足精度。

例题［8－1］ 已知某火箭发动机的有关参数为：f0＝RT0＝832.2k J／kg，γ＝1.253， ρp＝1610kg／m3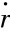；·＝apn＝3.4166×10-5p0.358m／s（其中p的单位为Pa）；装药在燃烧结束瞬间的燃烧面积Ab＝2.015m2；At＝4.64×10-3m2；取热损失修正系数χ＝0.9，质量流率系数φ·＝0.95。求燃烧结束瞬间燃烧室的平衡压强。

解： 已知比热比求得Γ＝0.6586； 侵蚀一般只发生在工作前期， 燃烧结束时φ（ ）＝1.0， 则该瞬时的装填参量为

取δ（1）＝0，则

用p（1）eq计算得δ（2）则

同理，得

以上计算过程可以一直进行下去， 直到满足精度要求为止。 可见， 忽略δ在本例中带来的误差约1.4％。