随机变量条件概率与全概率公式

中心极限定理是研究独立随机变量和的极限分布为正态分布的命题．大数定律仅仅从定性的角度解决了频率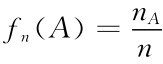稳定于概率p，即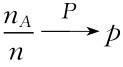，为了定量地估计用频率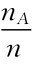估计概率P（A）（记为p）的误差，历史上De Moivre、Laplace等数学家经过许多努力，证明了n A的标准化随机变量渐近于N（0，1）分布．

在介绍正态分布时曾说过，许多随机现象，如测量误差，射击偏差等都可用正态分布来描述．经过长期观察、总结、发现那些服从正态分布的随机现象往往是由许多彼此无关，谁也不起突出作用，只均匀地起微小作用的随机因素共同作用而产生．换句话说，这类随机现象往往可视为独立（或弱相依）随机变量之和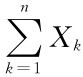＝，在什么条件下有渐近正态分布的问题，在长达两个世纪的时间内成为概率论讨论的中心课题，为使问题规范化，数学家们将问题归结为讨论规范和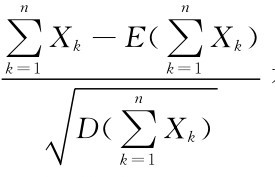有渐近分布N（0，1）的条件，并称有此结论的随机序列｛Xn｝服从中心极限定理．

定理5．2．1 林德贝格－勒维中心极限定理，又称独立同分布的中心极限定理

设｛Xn｝是独立同分布（i．i．d．）的随机变量序列，且E（Xi）＝μ，Var（Xi）＝σ2＞0．i＝1，2，…，n，…，则随机变量Zn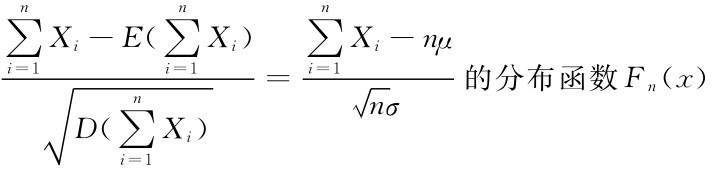＝收敛于标准正态分布的分布函数Φ（x）．即对于任意的实数x有

定理的证明略．

注5．2．1 设｛Xn｝是独立同分布的随机变量序列，且E（Xi）＝μ，Var（Xi）＝σ2＞0，则当n充分大时，有（1）随机变量Yn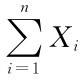＝近似地服从N（nμ，nσ2）；（2 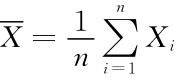）近似服从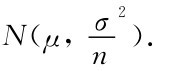

例5．2．1 某单位内部有260部电话分机，每个分机有4％的时间要使用外线通话，设每个电话分机是否使用外线通话是相互独立的．问该单位总机至少需要安装多少条外线才能以95％以上的概率保证每个电话分机在使用外线时不用等候？

解 令Xk＝，k＝1，2，…，n，并记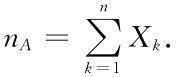

则n A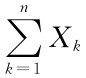＝表示同时使用外线通话的电话总数，此处n＝260，p＝P｛Xk＝1｝＝0．04，np＝10．4，np（1－p）＝9．984．则根据题意应确定最小的b使P｛n A≤b｝≥95％成立．由上面的定理知

于是只要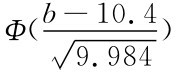≥0．95即可．查标准正态分布表得Φ（1．65）＝0．9505＞0．95，故取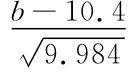＝1．65．解得b＝15．61．

所以，至少需要16条外线才能以95％以上的概率保证每个电话分机在使用外线时不用等候．

例5．2．2 用包装机包装糖果，则每袋净重为随机变量，设期望值为100克，标准差为10克，一箱内装200袋糖果．求一箱糖果净重大于20500克的概率．

解 设一箱糖果净重为X克，箱中第k袋糖果的净重为Xk克，k＝1，2，…，200．显

则

定理5．2．2 德莫佛－拉普拉斯中心极限定理 设在独立试验序列中，事件A发生的概率为p（0＜p＜1），随机变量n A表示事件A在n次试验中发生的次数．则对任意实数x，有

证 令Xi＝，i＝1，2，…，n

则随机变量Xi，i＝1，2，…，n为独立同分布的随机变量序列，都服从相同的“0－1”分布，且有E（Xi）＝p，D（Xi）＝p（1－p），i＝1，2，…，n，…，显然有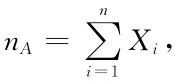故由定理5．2．1知

注5．2．2 注意到定理5．2．2中，n A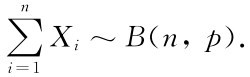＝德莫佛－拉普拉斯中心极限定理说明：当n充分大时，服从二项分布的随机变量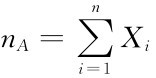将近似地服从正态分布．一般来说，当n较大时，二项分布的概率计算非常复杂，这时我们可以用正态分布来近似地计算二项分布．计算公式为

例5．2．3 某电站供应10000户居民用电，设在高峰时每户用电的概率为0．8，且各户用电量多少是相互独立的．求：

（1）同一时刻有8100户以上用电的概率．

（2）若每户用电功率为100W，则电站至少需要多少电功率才能保证以0．975的概率供应居民用电？

解 （1）设随机变量n A表示在10000户中同时用电的用户，则n A～B（10000，0．8），

于是np＝10000×0．8＝8000，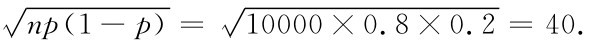

所求概率为

（2）若每户用电功率为100W，则n A户用电功率为100n AW．设供电站功率为QW，则由题意得

查表可知Φ（1．96）＝0．975，故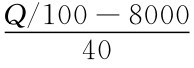＝1．96，Q＝807840．所以，电站供电功率不应少于807．84k W．