三大抽样分布

统计量是对总体的分布函数或数字特征进行统计推断的最重要的基本概念，所以寻求统计量的分布成为数理统计的基本问题之一．我们把统计量的分布称为抽样分布．然而要求出一个统计量的精确分布是十分困难的．而在实际问题中，大多数总体都服从正态分布．而对于正态分布，我们可以求出一些重要统计量的精确分布，如χ2分布，t分布和F分布，我们将这三大分布统称为“统计三大抽样分布”．

1．卡方分布

定义6．2．1 设（X1，X2，…，Xn）是来自总体X～N（0，1）的一个样本，则称统计量：

χ2＝所服从的分布是自由度为n的χ2（卡方）分布，记作：χ2～χ2（n）．

χ2（n）的概率密度函数为：

其中：

显然，χ2（x，n）≥0，且，即符合密度函数性质．

定理6．2．1 （χ2分布的性质）

（1）χ2分布的可加性：设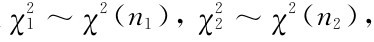且与相互独立，则：～χ2（n1＋n2）

（2）若χ2～χ2（n），则E（χ2）＝n，D（χ2）＝2n．

事实上，因为Xi～N（0，1），则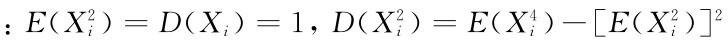－1＝3－1＝2，i＝1，2，…，n，所以，E（χ2）＝E＝

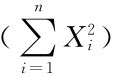定义6．2．2 （上α分位数）设随机变量X的分布函数为F（x），对于给定的正数α（0＜α＜1），若有xα满足P｛X≥xα｝＝α，则称xα为X的上α分位数（或上α分位点）．

定义6．2．3 （χ2分布上α分位数）对于不同自由度n及不同的数α（0＜α＜1），定义是自由度为n的χ2分布上α分位数，如果其满足

图6－1

图像描述参见图6－1．

χ2分布上α分位数的值可以通过查表得出，当n较大（n＞45）时，有近似公式（n）≈（uα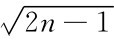＋）2，其中uα为标准正态分布的上α分位数．

2．t分布

定义6．2．4 设X～N（0，1），Y～χ2（n），且X与Y相互独立，则称统计量：T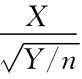＝所服从的分布是自由度为n的t分布，记为T～t（n），t分布又称为学生氏（Student）分布．

t分布图像的性质：（1）密度函数曲线关于x＝0对称；（2）密度函数在x＝0达最大值；

（3）密度函数曲线的水平渐近线为x轴．

（4）可以证明，当自由度n→∞时，t分布将趋于N（0，1）．

t分布的性质：

（1）若T～t（n），则n＞1时，E（T）＝0；n＞2时，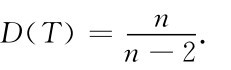

（2）可以证明，当自由度n→∞时，t分布将趋于N（0，1）．

（3）（上α分位数）对于不同的自由度n及不同的数α（0＜α＜1），定义tα是自由度为n的t分布上α分位数，如果其满足

图像描述参见图6－2．

（4）易证tα（n）＝－t1－α（n）；

（5）t（n）分布的α分位数tα（n）可以由附表查出其值．

由于n＞30时，t（n）分布接近于N（0，1），所以当n＞45时，可查N（0，1）分布分位数表．

3．F分布

定义6．2．5 设X～χ2（n1），Y～χ2（n2），且X与Y相互独立，则称统计量服从自由度为n1和n2的F分布，记作：F～F（n1，n2）．

图6－2

F分布的概率密度为

注6．1．3 （1）F分布的密度函数图形与χ2分布的密度函数图形类似，是一个只取非负值的偏态分布．

（2）（上α分位数）对于不同的自由度n1和n2及不同的数α（0＜α＜1），定义Fα是自由度为n1和n2的F分布上α分位数，如果其满足

图像描述参见图6－3．

图6－3

容易证明，F1－α（n1，n2）·Fα（n2，n1）＝1．

例6．2．1 设总体X～N（0，1），X1，X2，…，X6为来自总体X的一个样本，又设Y＝（X1＋X2＋X3）2＋（X4＋X5＋X6）2，试确定C，使得CY服从χ2分布．

解 由已知条件及正态分布的独立性有：X1＋X2＋X3与X4＋X5＋X6相互独立，且满足

X1＋X2＋X3～N（0，3），X4＋X5＋X6～N（0，3）

从而

由于

故当C＝1／3时，CY＝（2），故所求C值为1／3．

例6．2．2 设正态总体X～N（0，22），X1，X2，…，X15为来自总体X的一个样本，且

试确定随机变量Y的分布．

解 由于X～N（0，22），故X／2～N（0，1），从而由已知条件有

于是由F分布的定义有：